题目链接:点我啊╭(╯^╰)╮
参考博客:点我啊╭(╯^╰)╮
题目大意:
线段树的左右子区间为 [ l , ? l + r 2 ? ] [l, \lfloor \frac{l+r}{2} \rfloor] [l,?2l+r??]、 [ l , ? l + 2 2 ? ] [l, \lceil \frac{ l+2 }{ 2 } \rceil] [l,?2l+2??]
定义 f ( i , n ) f(i, n) f(i,n) 为在长度为 n n n 的线段树上标号为 i i i 的叶子结点的深度,求
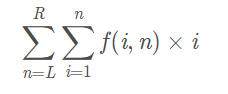
解题思路:
f n f_n fn? 为 有 n n n 个叶子的线段树的叶子深度和
g n g_n gn? 为 叶子深度叶子 i d id id 的和
h n h_n hn? 为 叶子深度乘 n n n 的和
F n 、 G n 、 H n F_n、G_n、H_n Fn?、Gn?、Hn?分别为它们的前缀和
根据线段树的特性,将每颗线段树分为两颗子树
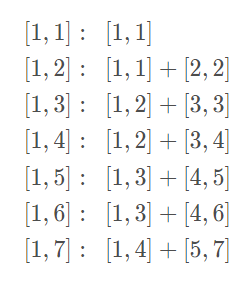
根据性质可得出以下递推式:
当 n n n 为奇数时, l = ? n 2 ? l = \lceil \frac{ n }{ 2 } \rceil l=?2n?? 、 r = ? n 2 ? r = \lfloor \frac{ n }{ 2 } \rfloor r=?2n??
F [ n ] = F [ l ] + F [ r ] ? 3 + n ( n + 1 ) 2 ? 1 F[n] = F[l] + F[r]*3 + \frac{ n(n+1) }{ 2 } - 1 F[n]=F[l]+F[r]?3+2n(n+1)??1
H [ n ] = ( H [ l ] ? 2 ? F [ l ] ) + H [ r ] ? 2 + ( H [ r ] ? 2 + F [ r ] ) + H [ r ] ? 2 + n ( n + 1 ) ( 2 n + 1 ) 6 ? 1 H[n] = (H[l]*2 - F[l]) + H[r]*2 + (H[r]*2 + F[r]) + H[r]*2 + \frac{ n(n+1)(2n+1) }{ 6 } - 1 H[n]=(H[l]?2?F[l])+H[r]?2+(H[r]?2+F[r])+H[r]?2+6n(n+1)(2n+1)??1
G [ n ] = ( G [ l ] + G [ r ] ) + ( G [ r ] + H [ r ] ) + ( G [ r ] + H [ r ] + F [ r ] ) + ∑ i = 2 n i ( i + 1 ) 2 G[n] = (G[l] + G[r]) + (G[r] + H[r]) + (G[r] + H[r] + F[r]) + \sum_{i=2}^{n}\frac{ i(i+1) }{ 2 } G[n]=(G[l]+G[r])+(G[r]+H[r])+(G[r]+H[r]+F[r])+∑i=2n?2i(i+1)?
当 n n n 为偶数时, l = n 2 l = \frac{ n }{ 2 } l=2n? 、 r = n 2 ? 1 r = \frac{ n }{ 2 } - 1 r=2n??1
F [ n ] = F [ l ] ? 3 + F [ r ] + n ( n + 1 ) 2 ? 1 F[n] = F[l]*3 + F[r] + \frac{ n(n+1) }{ 2 } - 1 F[n]=F[l]?3+F[r]+2n(n+1)??1
H [ n ] = H [ l ] ? 2 + ( H [ l ] ? 2 ? F [ l ] ) + H [ l ] ? 2 + ( H [ r ] ? 2 + F [ r ] ) + n ( n + 1 ) ( 2 n + 1 ) 6 ? 1 H[n] = H[l]*2 + (H[l]*2 - F[l]) + H[l]*2 + (H[r]*2 + F[r]) + \frac{ n(n+1)(2n+1) }{ 6 } - 1 H[n]=H[l]?2+(H[l]?2?F[l])+H[l]?2+(H[r]?2+F[r])+6n(n+1)(2n+1)??1
G [ n ] = G [ l ] ? 2 + ( G [ l ] + H [ l ] ) + ( G [ r ] + H [ r ] + F [ r ] ) + ∑ i = 2 n i ( i + 1 ) 2 G[n] = G[l]*2 + (G[l] + H[l]) + (G[r] + H[r] + F[r]) + \sum_{i=2}^{n}\frac{ i(i+1) }{ 2 } G[n]=G[l]?2+(G[l]+H[l])+(G[r]+H[r]+F[r])+∑i=2n?2i(i+1)?
证明过程自己脑补
核心:神TM简单的分形题
#include<bits/stdc++.h>
#define rint register int
#define deb(x) cerr<<#x<<" = "<<(x)<<'\n';
#define x first
#define y second
using namespace std;
typedef long long ll;
using pii = pair <int,int>;
const ll p = 998244353;
int T;
ll L, R, inv2, inv6;
map <ll, ll> f, h, g;ll qpow(ll a, ll b){ll ret = 1;while(b){if(b & 1) ret = ret * a % p;a = a * a % p;b >>= 1;}return ret;
}ll sum1(ll n){return (n %= p) * (n + 1) % p * inv2 % p;
}
ll sum2(ll n){return (n %= p) * (n + 1) % p * (n*2 + 1) % p * inv6 % p;
}
ll sum3(ll n){return (sum1(n) + sum2(n)) % p * inv2 % p;
}void dfs(ll n){if(f.count(n)) return;if(n <= 1) {f[n] = h[n] = g[n] = n;return;}if(n & 1){ll l = (n + 1) >> 1, r = n >> 1;dfs(l), dfs(r);f[n] = (f[l] + f[r]*3 + sum1(n) - 1 + p) % p;h[n] = ((h[l]*2 - f[l]) + h[r]*2 + (h[r]*2 + f[r]) + h[r]*2 + sum2(n) - 1 + p) % p;g[n] = ((g[l] + g[r]) + (g[r] + h[r]) + (g[r] + h[r] + f[r]) + sum3(n) - 1 + p) % p;} else {ll l = n >> 1, r = l - 1;dfs(l), dfs(r);f[n] = (f[l]*3 + f[r] + sum1(n) - 1 + p) % p;h[n] = (h[l]*2 + (h[l]*2 - f[l]) + h[l]*2 + (h[r]*2 + f[r]) + sum2(n) - 1 + p) % p;g[n] = (g[l]*2 + (g[l] + h[l]) + (g[r] + h[r] + f[r]) + sum3(n) - 1 + p) % p;}
}ll cal(ll x){dfs(x);return g[x];
}int main() {inv2 = qpow(2, p - 2);inv6 = qpow(6, p - 2);scanf("%d", &T);while(T--){scanf("%lld%lld", &L, &R);printf("%lld\n", (cal(R) - cal(L - 1) + p * 2) % p);}
}