题目描述

题解
这道题难就难在这一个均方差公式怎么搞,我们不妨对这一个算式进行化简。
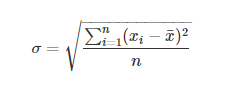
= ∑ ( x i 2 ? 2 ? x i ? x ? + n ? x ? 2 ) n =\sqrt \frac{\sum (x_i^2-2*x_i*\overline x+n*\overline x^2)}{n} =n∑(xi2??2?xi??x+n?x2)??
= ∑ x i 2 ? 2 ? ∑ x i ? x ? + n ? x ? 2 n =\sqrt \frac{\sum x_i^2-2*\sum x_i*\overline x+n*\overline x^2}{n} =n∑xi2??2?∑xi??x+n?x2??
= ∑ x i 2 ? 2 ? n ? x ? ? x ? + n ? x ? ? x ? n =\sqrt \frac{\sum x_i^2-2*n*\overline x*\overline x+n*\overline x*\overline x}{n} =n∑xi2??2?n?x?x+n?x?x??
= ∑ x i 2 ? n ? x ? ? x ? n =\sqrt \frac{\sum x_i^2-n*\overline x*\overline x}{n} =n∑xi2??n?x?x??
= ∑ x i 2 n ? x ? 2 =\sqrt{\frac{\sum x_i^2}{n}-\overline x^2} =n∑xi2???x2?
推到这里就很简洁明了啦!我们只要求解 ∑ x i \sum x_i ∑xi?的最小值即可。也就是每一个区域的平方和最小,这个用平面DP的方法可以很简单的得到,这里就不说了。
代码如下:
#include <iostream>
#include <cstdio>
#include <cmath>using namespace std;
const int N = 10;int n = 8, m;
int a[N][N], f[N][N][N][N][20];int s(int A,int b,int c,int d)
{
int sum = a[c][d] - a[A-1][d] - a[c][b-1] + a[A-1][b-1];return sum * sum;
}int main(void)
{
freopen("input.in","r",stdin);freopen("output.out","w",stdout);cin >> m;for (int i=1;i<=n;++i)for (int j=1;j<=n;++j)cin>>a[i][j], a[i][j] = a[i-1][j]+a[i][j-1]-a[i-1][j-1]+a[i][j];for (int r=1;r<=m;++r)for (int i=1;i<=n;++i)for (int j=1;j<=n;++j)for (int k=i;k<=n;++k)for (int t=j;t<=n;++t){
if (r == 1) {
f[i][j][k][t][r] = s(i,j,k,t); continue; };f[i][j][k][t][r] = 1e9;for (int p=i;p<k;++p) f[i][j][k][t][r] = min(f[i][j][k][t][r],f[i][j][p][t][r-1]+s(p+1,j,k,t));for (int p=i;p<k;++p) f[i][j][k][t][r] = min(f[i][j][k][t][r],f[p+1][j][k][t][r-1]+s(i,j,p,t));for (int p=j;p<t;++p) f[i][j][k][t][r] = min(f[i][j][k][t][r],f[i][j][k][p][r-1]+s(i,p+1,k,t));for (int p=j;p<t;++p) f[i][j][k][t][r] = min(f[i][j][k][t][r],f[i][p+1][k][t][r-1]+s(i,j,k,p)); }int ans = f[1][1][8][8][m];int sum = s(1,1,8,8);printf("%.3lf",sqrt(ans*1.0/(m*1.0)-sum*1.0/(m*m*1.0)));return 0;
}