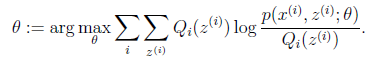问题
之前我们考虑的训练数据中样例![]() 的个数m都远远大于其特征个数n,这样不管是进行回归、聚类等都没有太大的问题。然而当训练样例个数m太小,甚至m<<n的时候,使用梯度下降法进行回归时,如果初值不同,得到的参数结果会有很大偏差(因为方程数小于参数个数)。另外,如果使用多元高斯分布(Multivariate Gaussian distribution)对数据进行拟合时,也会有问题。让我们来演算一下,看看会有什么问题:
的个数m都远远大于其特征个数n,这样不管是进行回归、聚类等都没有太大的问题。然而当训练样例个数m太小,甚至m<<n的时候,使用梯度下降法进行回归时,如果初值不同,得到的参数结果会有很大偏差(因为方程数小于参数个数)。另外,如果使用多元高斯分布(Multivariate Gaussian distribution)对数据进行拟合时,也会有问题。让我们来演算一下,看看会有什么问题:
多元高斯分布的参数估计公式如下:
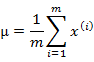
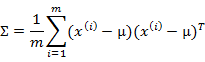
分别是求mean和协方差的公式,![]() 表示样例,共有m个,每个样例n个特征,因此
表示样例,共有m个,每个样例n个特征,因此![]() 是n维向量,
是n维向量,![]() 是n*n协方差矩阵。
是n*n协方差矩阵。
当m<<n时,我们会发现![]() 是奇异阵(
是奇异阵(![]() ),也就是说
),也就是说![]() 不存在,没办法拟合出多元高斯分布了,确切的说是我们估计不出来
不存在,没办法拟合出多元高斯分布了,确切的说是我们估计不出来![]() 。
。
如果我们仍然想用多元高斯分布来估计样本,那怎么办呢?
限制协方差矩阵
当没有足够的数据去估计![]() 时,那么只能对模型参数进行一定假设,之前我们想估计出完全的
时,那么只能对模型参数进行一定假设,之前我们想估计出完全的![]() (矩阵中的全部元素),现在我们假设
(矩阵中的全部元素),现在我们假设![]() 就是对角阵(各特征间相互独立),那么我们只需要计算每个特征的方差即可,最后的
就是对角阵(各特征间相互独立),那么我们只需要计算每个特征的方差即可,最后的![]() 只有对角线上的元素不为0
只有对角线上的元素不为0
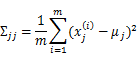
回想我们之前讨论过的二维多元高斯分布的几何特性,在平面上的投影是个椭圆,中心点由![]() 决定,椭圆的形状由
决定,椭圆的形状由![]() 决定。
决定。![]() 如果变成对角阵,就意味着椭圆的两个轴都和坐标轴平行了。
如果变成对角阵,就意味着椭圆的两个轴都和坐标轴平行了。
如果我们想对![]() 进一步限制的话,可以假设对角线上的元素都是等值的。
进一步限制的话,可以假设对角线上的元素都是等值的。
![]()
其中
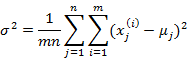
也就是上一步对角线上元素的均值,反映到二维高斯分布图上就是椭圆变成圆。
当我们要估计出完整的![]() 时,我们需要m>=n+1才能保证在最大似然估计下得出的
时,我们需要m>=n+1才能保证在最大似然估计下得出的![]() 是非奇异的。然而在上面的任何一种假设限定条件下,只要m>=2都可以估计出限定的
是非奇异的。然而在上面的任何一种假设限定条件下,只要m>=2都可以估计出限定的![]() 。
。
这样做的缺点也是显然易见的,我们认为特征间独立,这个假设太强。接下来,我们给出一种称为因子分析的方法,使用更多的参数来分析特征间的关系,并且不需要计算一个完整的![]() 。
。
边缘和条件高斯分布
在讨论因子分析之前,先看看多元高斯分布中,条件和边缘高斯分布的求法。这个在后面因子分析的EM推导中有用。
假设x是有两个随机向量组成(可以看作是将之前的![]() 分成了两部分)
分成了两部分)
![]()
其中![]() ,
,![]() ,那么
,那么![]() 。假设x服从多元高斯分布
。假设x服从多元高斯分布![]() ,其中
,其中
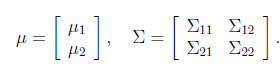
其中![]() ,
,![]() ,那么
,那么![]() ,
,![]() ,由于协方差矩阵是对称阵,因此
,由于协方差矩阵是对称阵,因此![]() 。
。
整体看来![]() 和
和![]() 联合分布符合多元高斯分布。
联合分布符合多元高斯分布。
那么只知道联合分布的情况下,如何求得![]() 的边缘分布呢?从上面的
的边缘分布呢?从上面的![]() 和
和![]() 可以看出,
可以看出,
![]() ,
,![]() ,下面我们验证第二个结果
,下面我们验证第二个结果
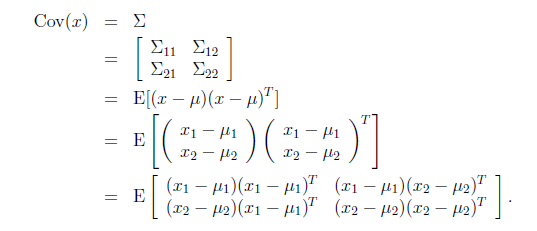
由此可见,多元高斯分布的边缘分布仍然是多元高斯分布。也就是说![]() 。
。
上面Cov(x)里面有趣的是![]() ,这个与之前计算协方差的效果不同。之前的协方差矩阵都是针对一个随机变量(多维向量)来说的,而
,这个与之前计算协方差的效果不同。之前的协方差矩阵都是针对一个随机变量(多维向量)来说的,而![]() 评价的是两个随机向量之间的关系。比如
评价的是两个随机向量之间的关系。比如![]() ={身高,体重},
={身高,体重},![]() ={性别,收入},那么
={性别,收入},那么![]() 求的是身高与身高,身高与体重,体重与体重的协方差。而
求的是身高与身高,身高与体重,体重与体重的协方差。而![]() 求的是身高与性别,身高与收入,体重与性别,体重与收入的协方差,看起来与之前的大不一样,比较诡异的求法。
求的是身高与性别,身高与收入,体重与性别,体重与收入的协方差,看起来与之前的大不一样,比较诡异的求法。
上面求的是边缘分布,让我们考虑一下条件分布的问题,也就是![]() 的问题。根据多元高斯分布的定义,
的问题。根据多元高斯分布的定义,![]() 。
。
且
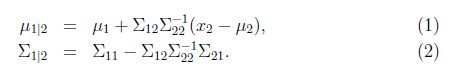
这是我们接下来计算时需要的公式,这两个公式直接给出,没有推导过程。如果想了解具体的推导过程,可以参见Chuong B. Do写的《Gaussian processes》。
因子分析例子
下面通过一个简单例子,来引出因子分析背后的思想。
因子分析的实质是认为m个n维特征的训练样例![]() 的产生过程如下:
的产生过程如下:
1、 首先在一个k维的空间中按照多元高斯分布生成m个![]() (k维向量),即
(k维向量),即
![]()
2、 然后存在一个变换矩阵![]() ,将
,将![]() 映射到n维空间中,即
映射到n维空间中,即
![]()
因为![]() 的均值是0,映射后仍然是0。
的均值是0,映射后仍然是0。
3、 然后将![]() 加上一个均值
加上一个均值![]() (n维),即
(n维),即
![]()
对应的意义是将变换后的![]() (n维向量)移动到样本
(n维向量)移动到样本![]() 的中心点
的中心点![]() 。
。
4、 由于真实样例![]() 与上述模型生成的有误差,因此我们继续加上误差
与上述模型生成的有误差,因此我们继续加上误差![]() (n维向量),
(n维向量),
而且![]() 符合多元高斯分布,即
符合多元高斯分布,即
![]()
![]()
5、 最后的结果认为是真实的训练样例![]() 的生成公式
的生成公式
![]()
让我们使用一种直观方法来解释上述过程:
假设我们有m=5个2维的样本点![]() (两个特征),如下:
(两个特征),如下:
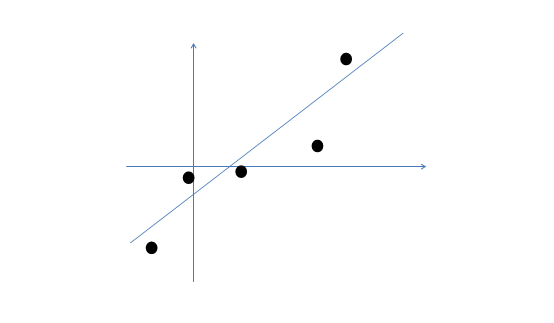
那么按照因子分析的理解,样本点的生成过程如下:
1、 我们首先认为在1维空间(这里k=1),存在着按正态分布生成的m个点![]() ,如下
,如下
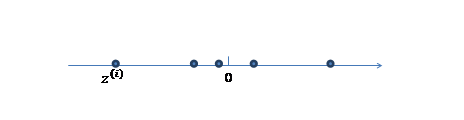
均值为0,方差为1。
2、 然后使用某个![]() 将一维的z映射到2维,图形表示如下:
将一维的z映射到2维,图形表示如下:
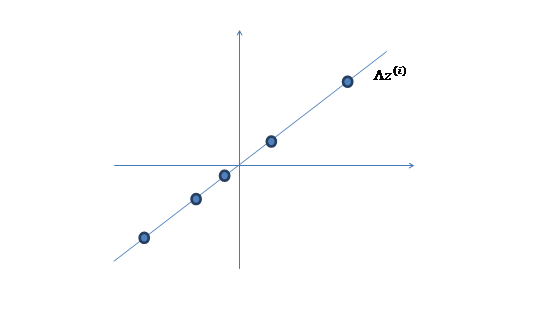
3、 之后加上![]() ,即将所有点的横坐标移动
,即将所有点的横坐标移动![]() ,纵坐标移动
,纵坐标移动![]() ,将直线移到一个位置,使得直线过点
,将直线移到一个位置,使得直线过点![]() ,原始左边轴的原点现在为
,原始左边轴的原点现在为![]() (红色点)。
(红色点)。
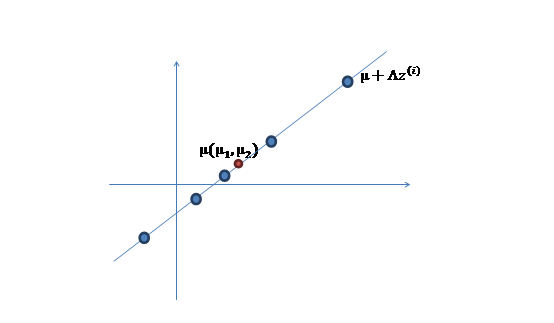
然而,样本点不可能这么规则,在模型上会有一定偏差,因此我们需要将上步生成的点做一些扰动(误差),扰动![]() 。
。
4、 加入扰动后,我们得到黑色样本![]() 如下:
如下:
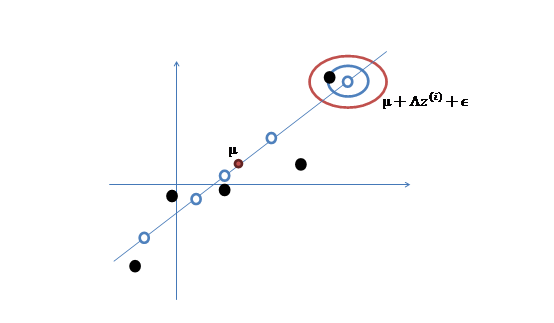
5、 其中由于z和![]() 的均值都为0,因此
的均值都为0,因此![]() 也是原始样本点(黑色点)的均值。
也是原始样本点(黑色点)的均值。
由以上的直观分析,我们知道了因子分析其实就是认为高维样本点实际上是由低维样本点经过高斯分布、线性变换、误差扰动生成的,因此高维数据可以使用低维来表示。
因子分析模型
上面的过程是从隐含随机变量z经过变换和误差扰动来得到观测到的样本点。其中z被称为因子,是低维的。
我们将式子再列一遍如下:
![]()
![]()
![]()
其中误差![]() 和z是独立的。
和z是独立的。
下面使用的因子分析表示方法是矩阵表示法,在参考资料中给出了一些其他的表示方法,如果不明白矩阵表示法,可以参考其他资料。
矩阵表示法认为z和x联合符合多元高斯分布,如下
![]()
求![]() 之前需要求E[x]
之前需要求E[x]
![]()
![]()
![]()
我们已知E[z]=0,因此
![]()
下一步是计算![]() ,
,
其中![]()
接着求![]()
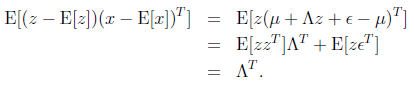
这个过程中利用了z和![]() 独立假设(
独立假设(![]() )。并将
)。并将![]() 看作已知变量。
看作已知变量。
接着求![]()
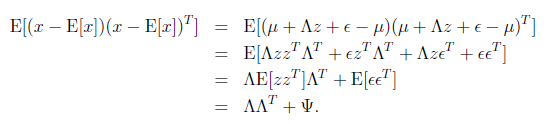
然后得出联合分布的最终形式
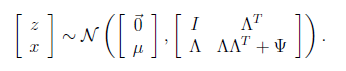
从上式中可以看出x的边缘分布![]()
那么对样本![]() 进行最大似然估计
进行最大似然估计
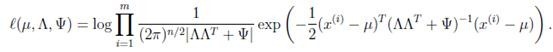
然后对各个参数求偏导数不就得到各个参数的值了么?
可惜我们得不到closed-form。想想也是,如果能得到,还干嘛将z和x放在一起求联合分布呢。根据之前对参数估计的理解,在有隐含变量z时,我们可以考虑使用EM来进行估计。
因子分析的EM估计
我们先来明确一下各个参数,z是隐含变量,![]() 是待估参数。
是待估参数。
回想EM两个步骤:
| 循环重复直到收敛 { (E步)对于每一个i,计算
(M步)计算
|
我们套用一下:
(E步):
![]()
根据第3节的条件分布讨论,
![]()
因此
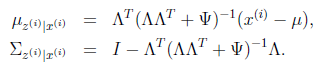
那么根据多元高斯分布公式,得到
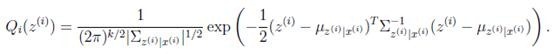
(M步):
直接写要最大化的目标是
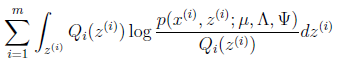
其中待估参数是![]()
下面我们重点求![]() 的估计公式
的估计公式
首先将上式简化为:
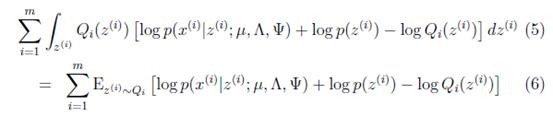
这里![]() 表示
表示![]() 服从
服从![]() 分布。然后去掉与
分布。然后去掉与![]() 不相关的项(后两项),得
不相关的项(后两项),得
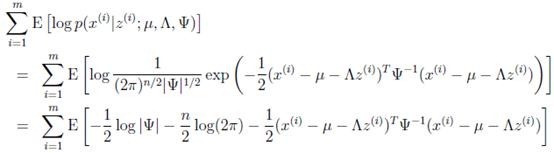
去掉不相关的前两项后,对![]() 进行导,
进行导,
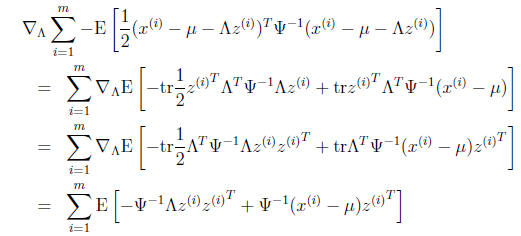
第一步到第二步利用了tr a = a(a是实数时)和tr AB = tr BA。最后一步利用了
tr就是求一个矩阵对角线上元素和。
最后让其值为0,并且化简得
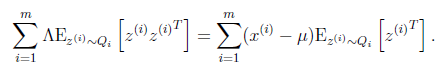
然后得到
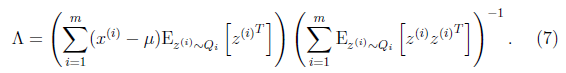
到这里我们发现,这个公式有点眼熟,与之前回归中的最小二乘法矩阵形式类似
![]()
这里解释一下两者的相似性,我们这里的x是z的线性函数(包含了一定的噪声)。在E步得到z的估计后,我们找寻的![]() 实际上是x和z的线性关系。而最小二乘法也是去找特征和结果直接的线性关系。
实际上是x和z的线性关系。而最小二乘法也是去找特征和结果直接的线性关系。
到这还没完,我们需要求得括号里面的值
根据我们之前对z|x的定义,我们知道
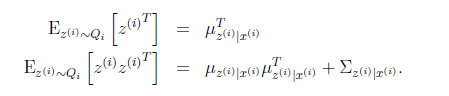
第一步根据z的条件分布得到,第二步根据![]() 得到
得到
将上面的结果代入(7)中得到
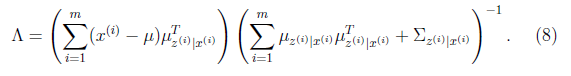
至此,我们得到了![]() ,注意一点是E[z]和
,注意一点是E[z]和![]() 的不同,后者需要求z的协方差。
的不同,后者需要求z的协方差。
其他参数的迭代公式如下:
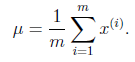
均值![]() 在迭代过程中值不变。
在迭代过程中值不变。
![]()
然后将![]() 上的对角线上元素抽取出来放到对应的
上的对角线上元素抽取出来放到对应的![]() 中,就得到了
中,就得到了![]() 。
。
总结
根据上面的EM的过程,要对样本X进行因子分析,只需知道要分解的因子数(z的维度)即可。通过EM,我们能够得到转换矩阵![]() 和误差协方差
和误差协方差![]() 。
。
因子分析实际上是降维,在得到各个参数后,可以求得z。但是z的各个参数含义需要自己去琢磨。
下面从一个ppt中摘抄几段话来进一步解释因子分析。
因子分析(factor analysis)是一种数据简化的技术。它通过研究众多变量之间的内部依赖关系,探求观测数据中的基本结构,并用少数几个假想变量来表示其基本的数据结构。这几个假想变量能够反映原来众多变量的主要信息。原始的变量是可观测的显在变量,而假想变量是不可观测的潜在变量,称为因子。
例如,在企业形象或品牌形象的研究中,消费者可以通过一个有24个指标构成的评价体系,评价百货商场的24个方面的优劣。
但消费者主要关心的是三个方面,即商店的环境、商店的服务和商品的价格。因子分析方法可以通过24个变量,找出反映商店环境、商店服务水平和商品价格的三个潜在的因子,对商店进行综合评价。而这三个公共因子可以表示为:
![]()
这里的![]() 就是样例x的第i个分量,
就是样例x的第i个分量,![]() 就是
就是![]() 的第i个分量,
的第i个分量,![]() 就是
就是![]() 的第i行第j列元素,
的第i行第j列元素,![]() 是z的第i个分量,
是z的第i个分量,![]() 是
是![]() 。
。
称![]() 是不可观测的潜在因子。24个变量共享这三个因子,但是每个变量又有自己的个性,不被包含的部分
是不可观测的潜在因子。24个变量共享这三个因子,但是每个变量又有自己的个性,不被包含的部分![]() ,称为特殊因子。
,称为特殊因子。
注意
因子分析与回归分析不同,因子分析中的因子是一个比较抽象的概念,而回归因子有非常明确的实际意义;
主成分分析分析与因子分析也有不同,主成分分析仅仅是变量变换,而因子分析需要构造因子模型。
主成分分析:原始变量的线性组合表示新的综合变量,即主成分;
因子分析:潜在的假想变量和随机影响变量的线性组合表示原始变量。
主成分分析和因子分析的区别http://cos.name/old/view.php?tid=10&id=82
因子分析PDF文件https://files-cdn.cnblogs.com/files/jerrylead/因子分析.pdf