4.2 笛卡尔坐标系
笛卡尔坐标系分为二维和三维坐标系
4.2.1二位坐标系
OpenGL 和 DirectX 二位坐标系是不同的,OpenGL 和 DirectX 是不同的图形访问接口,用来和硬件交互的

二维坐标系 是可以相互转换的,既 任意一个二维坐标系,都可以用由另一个二维坐标系通过旋转 得到,从这种意义上来说,所有的二维坐标系 都是等价的
4.2.2 三维坐标系
三维坐标系中的x ,y ,z 轴叫做该坐标系的 基矢量
如果这三个 基矢量 相互垂直 且 长度为1 ,则称为 标准基矢量
根据坐标轴方向的不同,分为左手坐标系 和 右手坐标系
旋向性:两个坐标系,可以通过 轴的旋转 重合,则具有相同的旋向性,否则具有不同的旋向性
左手坐标系和右手坐标系,具有不同的旋向性
4.2.3 左手坐标系
上面说了,根据 坐标轴的方向的不同,分为 左右手坐标系
左手坐标系 x 轴方向朝右,y 轴朝上, z 轴垂直于 xy 平面朝里

右手坐标系:
左手坐标系 x 轴方向朝左,y 轴朝上, z 轴垂直于 xy 平面朝里

4.2.4 unity中使用的坐标系
unity的坐标系 分为 模型坐标系 世界坐标系 观察坐标系 裁剪坐标系 屏幕坐标系 视口坐标系
其中 观察坐标系 使用的是右手坐标系 ,其它的均使用 左右坐标系
4.3 点和矢量
点 是二维或者三维空间中的一个位置,没有大小,方向等概念 ,二维中用P(x,y) , 三维中用(x,y,z) 表示
矢量 (也称为向量):具有 模(大小) 和 方向 的向量
标量:只有大小 没有方向
矢量可以认为是一个点相对于另一个点的偏移,是一个相对量。所以如果矢量的模和大小不变,无论放在哪里 ,都是一个矢量
4.3.1 点和矢量的区别
点是空间中的一个位置, 矢量是一个点相对于另一个点的偏移,如果把矢量的尾 固定在原点 ,矢量的表示和点的表示就一样了

4.3.2 矢量运算
包括 矢量的 加 减 ,矢量和标量 的乘除, 其中加减 可以认为是矢量的平移 ,乘除 是矢量的缩放
求矢量的模
4.3.3 单位矢量
单位矢量:是模为1的向量
一个向量转换成单位矢量的过程 叫 归一化
在计算光照时我们往往需要对向量进行归一化
单位矢量=向量/向量的模
零矢量:(0,0,0),其不能被归一化,以为分母不能为0
4.3.4 矢量的点积(点乘)
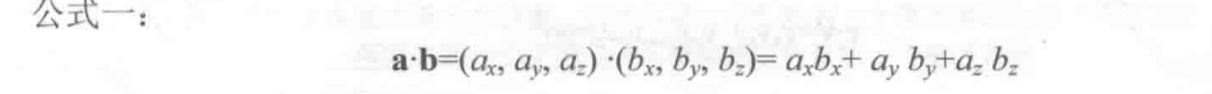
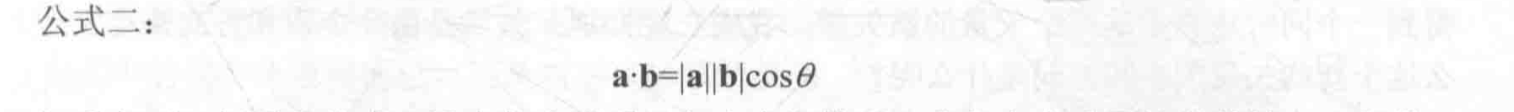
通过公式二 可以得知,如果 a b 都是单位矢量,则 a 点乘 b 就等于 二者之间夹角的余弦值 ,可以根据这个 判断两个向量之间的方向关系,a 在 b 的前方 还是后方,只要看余弦值是大于0 还是小于0 就行了
4.3.5 矢量的叉积(叉乘)
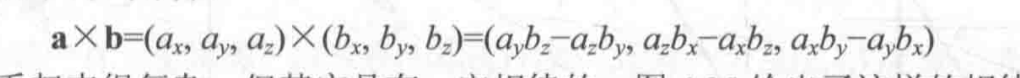
这是有规律的 ,分别是 a的y z x 乘以 b的z x y,每一个都往后错开一位,然后再相减
叉乘得到的是一个垂直于 a b 的向量
但是垂直于ab的向量的方向可以有两个,一个上 一个下, 这就要根据我们前面说的 左右手坐标系有关了,伸出右手,掌心方向和a 方向一样,大拇指方向,就是右手坐标系下 ab 叉乘后的向量的正方向

4.4 矩阵
4.4.1 矩阵和矢量的关系
矢量可以看成一个数组 ,矩阵也可以看成一个数组,这样矩阵就可以看成一个n*1 的列向量 或者 1*n 的行向量
4.4.2 矩阵的运算
矩阵包括 矩阵和标量指点的乘除
矩阵和矩阵之间的乘法

矩阵不满足交换律 既 AB 不等于 BA
满足结合律
4.4.3 方阵,对角元素,对角矩阵 等
方阵:列数和行数 相等的矩阵 比如 3x3 4x4
对角元素 :矩阵中行号和列号 相等的元素 称为对角元素 比如: m11 m22 m33
对角矩阵:除了对角元素 其它元素都为0的矩阵
单位矩阵:对角元素都为1的对角矩阵 称为单位矩阵 用 I 表示

单位矩阵和任何矩阵相乘 都等于 原矩阵
转置矩阵(transposed matrix):把原矩阵 行变列 ,这里写英文,是为了加深 unity里面求一个矩阵的转置矩阵的方法叫 transposed(M)

关于转置矩阵的性质

逆矩阵:一个矩阵是否有逆矩阵,前提该矩阵必须是方阵,这是充分非必要条件,是方阵可能有逆矩阵,不是方阵一定没有逆矩阵,零矩阵就没有逆矩阵,因为任何矩阵和它相乘,都是0 ,并不满足我们下面的条件

逆矩阵的性质

第一个 就相当于a 的倒数的倒数 还是 a
第二个 就相当于 1 的当属 还是1

性质三比较重要,性质四和转置矩阵的性质是一样的
求一个矩阵的逆矩阵 (增广法)
这个比较简单,也比较高效,所以选择了这个
主要原理:对原矩阵A(n阶) 右边加上一个等阶的单位矩阵E,变成W(A|E)矩阵(n*2n),对w 进行变换,最终变成(E|B),则B矩阵就是A 的逆矩阵
变换方法(高斯消元法)

既 每一行所进行的操作,只有乘以一个标量,再和该矩阵的另一行相加或相减 ,也可不进行加减操作,最后使得 左边矩阵为单位矩阵就行了
例如:
https://tieba.baidu.com/p/7311509555
正交矩阵:正交矩阵是方阵的一个特殊矩阵,如果一个方阵的转置矩阵和它相乘 等于 单位矩阵 ,就说他是正交的
性质:

第二个性质 是根据逆矩阵的性质得来的
判断一个矩阵是不是正交矩阵:


比如:

第一个 ,a(1,0,0) b(1,0,0) c(1,0,0) 都是单位矢量 但是 相互之间点乘不等于0
a 点乘 b 等于 1*1+0*0+0*0 =1 不等于0 所以 1 不是
同理 2、3 是正交矩阵
4.5 矩阵的几何意义 变换
线性变换:矢量加 和标量乘的变换

旋转 和 缩放 都是线性变换,如果只考虑旋转,一个3x3 的矩阵就可以表示所有的旋转

仿射变换:只考虑旋转和缩放是不现实的,有时候还要考虑 平移变换 因为平移变换不满足线性变换的条件,所以 结合了线性变换 和平移变换 的类型,就是仿射变换
仿射变换需要4维空间 ,也就是一个4x4 矩阵 ,这个4维空间 叫齐次坐标空间
4.5.1 齐次坐标
用4维空间,表示的坐标 叫齐次坐标 比如 p(x,y,z,w)
一个点 从三维坐标 变成 齐次坐标 只需要设置其 w 为1
一个矢量 从三维坐标 变成 齐次坐标 只需要设置其 w 为0,这是因为 矢量的平移 没有意义 ,只要矢量的模的大小 和 方向不发生变化,就是同一个矢量
4.5.2 基础变换矩阵
我们把纯旋转 ,缩放 ,平移的矩阵 称为 基础变换矩阵
它们有共同的特点 所以 把基础变换矩阵 分解成 4个部分

4.5.3 平移矩阵

点的 w 是1

方向矢量的 w 是0
所以 平移矩阵 的构成 应该是

上图 所示 是平移矩阵的 反方向平移矩阵,也就是 左上角 M矩阵 为单位矩阵 t 矩阵为平移的列向量
平移矩阵不是正交矩阵 ,因为不满足条件,条件可看上面
4.5.4 缩放矩阵

对点 缩放

对矢量 缩放
如果 kx=ky=kz ,既 缩放系数相等,称为统一缩放,否则称为非统一缩放
非同一缩放,会改变模型的比例
缩放矩阵的逆矩阵

4.5.5 旋转矩阵



4.5.6 复合变换(同时包含缩放 旋转 平移)
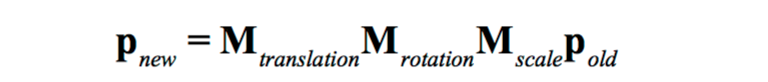
阅读顺序 从右往左
而 当旋转时 也是需要一个旋转顺序的 比如 给一个旋转角度(x,y,z),是先按 x 旋转还是先按y轴旋转,还是先按 z 轴旋转?
在 unity 里面 给出的顺序 是 zxy 既 先z 后 x 再 y

所以得出的旋转矩阵是上面的
这并不是写反了,因为按照 z x y 顺序旋转,也有两种旋转方式

第一种 每一次旋转都是独立的,不依赖于上次旋转的结果
第二种 旋转是相互依赖的,上次旋转的结果,影响下次旋转的结果
unity 中使用的是第一种,所以就没有左右之分了
4.6 坐标空间
4.6.1 坐标空间的转换
可以说每个事物都有自己的坐标空间,同时 它也是在另一个事物的坐标空间下 ,既 坐标空间是有层次的
坐标空间的转换,就发生在 点p 在知道A 坐标空间下的表示,需要得出在B空间下的表示



这里的 Oc Xc Yc Zc 都是子坐标空间下的点 在 父坐标空间 下的表示
这里的演算,只需要在纸上一画就知道了,比如 Ap 空间下 的 Cc 空间中有一点,Pc(1,1,0),
假设最简单的情况 两个坐标空间完全平行,Oc(2,2,0),则 Xc 的单位向量为 (3,3,0)-(3,2,0)=(1,0,0)
同理 Yc =(0,1,0) Zc=(0,0,1)
我们在图上很容易能看出来点P 在A坐标空间下的位置为(3,3,0) ,我们用上述公式验证一下 和我们已知的是一致的
最后得出来的空间变换矩阵为
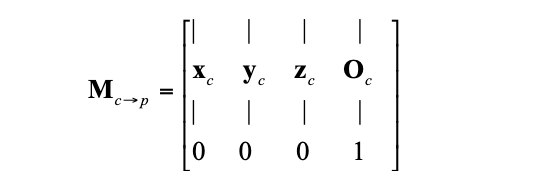



这里也验证了 上面的 推算公式 是正确的
4.6.4 模型空间
模型空间 变换到其它坐标空间,往往需要经过平移变换,所以要把模型坐标空间下的 点 转换为齐次坐标 向量的w 为1
4.6.5 世界空间

4.6.6 观察空间
观察空间 是右手坐标系,z轴的正方向,指向摄像机的后方
4.6.7 裁剪空间
裁剪空间 由 视锥体 决定
裁剪的目的 是为了方便渲染,处于视锥体内的图元被渲染,否则被剔除
所以 视锥体 会有两种,一种是 透视投影的视锥体,一种 正交投影的视锥体

最后的 点 在裁剪空间下的表示(透视投影)

点 是不是在 裁剪空间中的条件 是 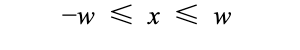
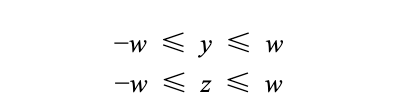
最后的 点 在裁剪空间下的表示(正交投影)

判断条件 和上面一样
4.6.8 屏幕空间
屏幕空间 是二维坐标系 ,OpenGL 和DirectX 坐标系 略有不同
把裁剪空间中的点 做一次 齐次除法 得到 归一化的设备坐标(NDC 这个以后会经常提及)
齐次除法 就是 x y z 分别除以 w
这个时候得到的 坐标位置 在[-1,1]之间


4.7 法线变换
法线变换 不能使用和 顶点变换 同一个变换矩阵 因为如果遇到非同一缩放,法线变换就会出错误
下面是 求 法线变换矩阵的推导公式

只有为单位向量 才能满足Ta * Na 为零向量

