万字详解决策树之ID3、CART、C4.5【原理+实例+代码实现】

决策树的含义

首先我们先来了解下什么是决策树。

上图就是一颗带有决策的树，其中天气、温度等称为特征，后面问号的位置称为阈值，如温度=35°，则阈值为35。

• 决策树是一种基本的分类与回归方法。这里主要讨论决策树用于分类。
• 决策树的结点和有向边分别表示
  1. 内部结点表示一个特征或者属性。
  2. 叶子结点表示一个分类。
  3. 有向边代表了一个划分规则。
• 决策树从根结点到子结点的的有向边代表了一条路径。
• 决策树的路径是互斥并且是完备的。
• 用决策树分类时，是对样本的某个特征进行测试，根据测试结果将样本分配
• 如果将样本分配到了树的子结点上，每个子结点对应该特征的一个取值。
• 决策树的优点：可读性强，分类速度快。
• 决策树学习通常包括3个步骤：
  1. 数据标注
  2. 特征选择。
  3. 决策树生成。
  4. 分类和识别。

决策树模型可以认为是if-then规则的集合。决策树学习的算法通常是遍历选择最优特征和特征值，并根据该特征对训练数据进行分割，使得对各个子数据集有一个最好的分类，这一过程对应着特征空间的划分，也对应着决策树的构建。

(信息熵+信息增益)&ID3

信息熵(Entropy)用来度量不确定性的，当熵越大，信息的不确定性越大，对于机器学习中的分类问题，那么，当前类别的熵越大，它的不确定性就越大

H(D)代表一个决策树的熵，熵的数学公式如下：

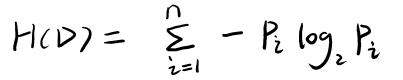
n是分类的数目，$p_i$是当前分类发生的概率。

细想一下，如果10个硬币，分类结果是10个正面，没有反面，那么信息熵为0，如下所示：

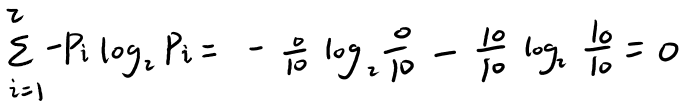
信息熵为0，就意味着信息确定，就意味着分类完成了。

在原有树的熵 H(D) 增加了一个分裂节点，使得熵变成了H(D|A)，则**信息增益(Information Gain，IG)**为：

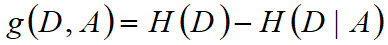
A是选择作为分裂依据的特征，g(D,A)也称为条件熵

即信息增益 = 分裂前的信息熵-分裂后的信息熵

也有更加准确的定义方法：

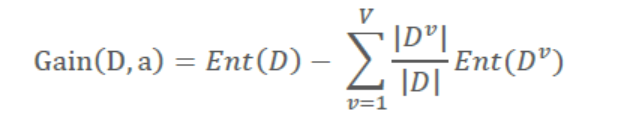
V表示根据特征a对样本集D划分(分裂)后，获得的总共类别数量(一般是二分类)；$D^v$表示每一个新类别中样本数量；Ent(D)和H(D)的含义相同，表示信息熵

我们以判断学生好坏的案例，计算信息熵和信息增益：

（1）在初始状态下，有10个学生，7个是好学生，3个不是好学生，计算树的信息熵(此时只有一个根节点) H(D)=0.88，如下所示：

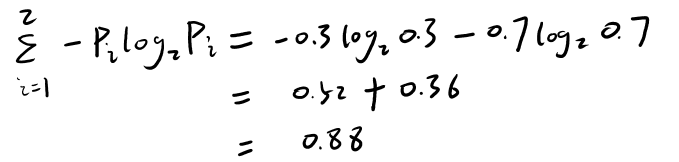
（2）我们根据分数这个特征对树进行分裂，设置分数的阈值为70，计算分裂后树的信息熵H(D|A1)=0.4344，如下所示：

（3）把(2)的特征有分数改为出勤率，设置出勤率阈值为75%，计算分裂后树的信息熵H(D|A2)=0.79，如下所示：

从上面的计算中，我们得到了3个熵：

• 在初始状态下，信息熵为0.88，
• 设置分数阈值为70进行分裂，信息熵为0.4344
• 设置出勤率阈值为75%进行分裂，信息熵为0.79

只要增加分裂节点后的熵比之前的熵小，那么就可以认为本次分裂是有效的，现在(2)和(3)的分裂都有效，但是哪个更好呢？
在设置分数阈值为70的熵比设置出勤率阈值为75%的熵要小，即前者分裂后数据比较纯一些，整个数据的确定性大了，因此设置分数阈值为70分裂方式效果更好，所以我们以该方式为基准进行分裂。

现在来计算信息增益，信息增益 = 分裂前的信息熵-分裂后的信息熵，计算如下所示：

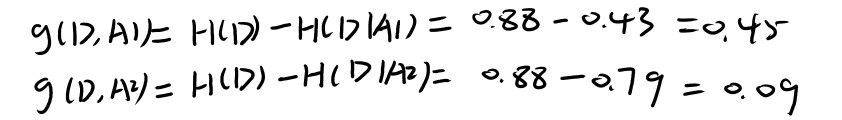
A1是以分数这个特征进行分裂，A2是以出勤率这个特征进行分裂

可以看到，以设置分数阈值为70进行分裂，信息增益更大。

信息增益在决策树算法中是用来选择特征的指标，信息增益越大，则这个特征的选择性越好，该特征具有更强的分类能力，如果一个特征的信息增益为0，则表示该特征没有什么分类能力。

ID3的原理：

利用数据标注和信息增益以及遍历，可以完成一个决策树中的特征和阈值的选择(得到最大信息增益的特征和阈值)，利用这三个(标注、信息增益、遍历)就可以完成一颗树，决策的树，分类的树，这个算法就是ID3()算法的思想

ID3(Iterative Dichotomisor 3) 迭代二分类三代，用信息增益准则选择特征，判定分类器的性能，从而构建决策树

经过上面的例子，可以得到如下结论：

• 只要分类后的总熵为0，那么这课树就训练完了（也就是分类完了）
• 熵在决策树中的作用：判断分类后，有没有达到我们的需求和目的，也就是数据是不是更加纯了，更加确定了。如果经过分类后，信息总熵的值更加小了，那么这次分类就是有效的。
• 熵越大，不确定就越大，分类未完成时，熵不为0
• 熵越小，分得越好，分类完成时，熵为0

根据上述思想，可以完成如下一颗树：

(纯度+基尼系数)&CART

在上面的例子中，我们是用决策树做分类的，那么做回归的时候该怎么做呢？ 现在把上述的分类结果由好学生换成是否为好学生的概率，如下所示：

分类的结果是概率，是个连续的变量，无法计算信息熵和信息增益了，这个时候怎么做呢？

为了解决这个问题，引入了纯度的概念。

纯度的定义如下：

?_? 和?_r 是按照某一特征分裂后，树的两个分裂结点各自占的比例，Var是方差，就是计算左侧和右侧部分的方差，y_i是具体的值(这里是好学生的概率)

纯度增益 = 分裂前的纯度 - 分裂后的纯度

可以看到，纯度和方差的定义大致一样(这里的纯度没有除以n，方差的定义需要除以n)，在有的文献中也称为偏差，其实含义都一样，都是表示数据的离散程度

细想一下，如果上述10个学生的是好学生的概率都一样(比如都是0.9)，那么纯度(方差)是0，说明数据完全没有离散性，非常的确定。

可以看到，纯度和信息熵所代表的含义是一样的，只不过熵表示分类信息的不确定性，纯度表示数据的离散程度，下面即将要介绍的基尼系数，表示的也是分类(CART的分类)信息的确定性

（1）在初始状态下，计算树的纯度(此时只有一个根节点) 纯度=0.4076，如下所示：

import numpy as np
a = [0.9,0.9,0.8,0.5,0.3,0.8,0.85,0.74,0.92,0.99]
a = np.array(a)
a_mean = np.mean(a)
# 不用除以n
a_va = np.sum(np.square(a-a_mean))
a_va
# 输出 0.4076000000000001

(2) 设置分数阈值为70进行分裂，计算纯度=0.2703，如下所示：

(3) 设置出勤率阈值为75%进行分类，计算纯度：

从上面的计算中，我们得到了3个纯度：

• 在初始状态下，纯度为0.4076，
• 设置分数阈值为70进行分裂，纯度为0.2703
• 设置出勤率阈值为75%进行分裂，纯度0.1048

从这三个纯度可以得知，这两种方式的分裂均有效，按照出勤率阈值=75%计算的纯度更小，说明分裂的效果更好，信息更确定了。

也可以计算出纯度的增益：

• 设置分数阈值为70进行分裂，纯度的增益为0.4079 - 0.2703 = 0.1376
• 设置出勤率阈值为75%进行分裂，纯度的增益为0.4079 - 0.1048 =0.3031

设置出勤率阈值为75%进行分裂得到纯度增益更大，说分裂效果更好(这里和信息熵及信息增益的原理是一样的)

思考：为什么决策树分类和回归的结果不同？
因为我们的标注不同，之前标注的是好学生与坏学生，现在重新标注了是好学生的概率，标注不同对我们模型训练的引导就不同，造成的结果就不同。

思考：将模型训练完之后怎么去得到具体回归的那个值呢？
如果最后只有一个结点，就是指这个结点的值，如果最后有多个结点，那应该是平均值

利用数据标注和纯度以及遍历，可以完成一个决策树中的特征和阈值的选择(得到最大信息增益的特征和阈值)，利用这三个(标注、纯度、遍历)就可以完成一颗树，决策的树，回归的树，这个算法就是CART的回归算法

CART做回归时用的是纯度，做分类时用的是基尼系数。

基尼系数

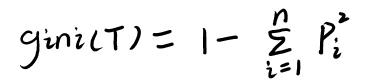
n代表n分类，$p_i$表示不同类别的概率

按照某一特征分裂后的基尼系数为：

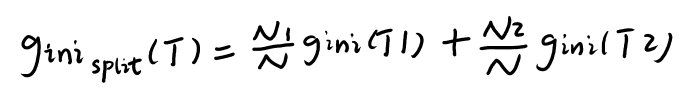
基尼增益 = 分裂前的基尼 - 分裂后的基尼

我们以硬币来举例子解释基尼系数，假设10个硬币做二分类，10个是正面，没有反面，那么基尼系数为：

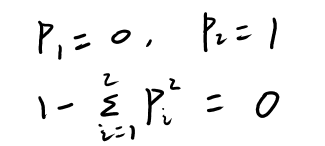
如果10个硬币做二分类，5个是正面，5个是反面，那么基尼系数为

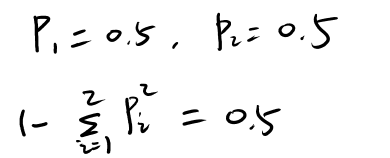
可以看到，当分类完成时，基尼系数为0，因此基尼系数与信息的含义类似，基尼系数越大，信息的不确定性就越大。

注意：基尼系数和信息熵都是用于分类的

然后，按照某一特征进行分裂，比如按照硬币的大小(或面值)进行分裂，计算分裂后的基尼系数，最后计算基尼增益，得到的基尼增益最大的特征和阈值就是我们要找的分裂方式。

纯度增益、基尼增益、信息增益的原理完全一样

CART（classification and regression tree）分类和回归树，分类是使用基尼系数判定分类器的性能，回归时使用纯度判定分类器的性能

信息增益率&C4.5

信息增益准则对可取值数目较多的特征有所偏好，为了减少这种偏好可能带来的不利影响，C4.5决策树算法使用了“增益率”：

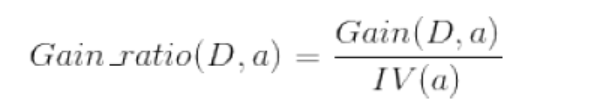
其中IV(a)称为特征a的“固有值”，称为特征a的分裂信息度量，其实就是特征a的信息熵(注意：这个和信息增益减去的按特征a分裂后的信息熵不一样，在下面具体例子中可看到)

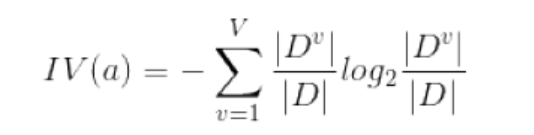
需要注意的是，信息增益率对可取值数目较少的特征所有偏好，因此，C4.5算法并不是直接选择信息增益率最大的特征进行分裂，而是使用了一个启发式：先找出信息增益高于平均水平的特征，再从中选择增益率最高的。 可以看出，使用信息增益率可以解决分裂后叶子结点过多的问题，从而解决过拟合

我们用下面的例子计算信息增益率(抱歉，没找到更清晰的图片)

（1）第一步：计算样本集D的信息熵

Ent(D) = -9/14*log2(9/14) – 5/14*log2(5/14) = 0.940
Ent(D)表示熵，也可以H(D)表示

（2）第二步：依据每个特征划分样本集D，并计算每个特征（划分样本集D后）的信息熵

• Ent(天气) = 5/14*[-2/5*log2(2/5)-3/5*log2(3/5)] + 4/14*[-4/4*log2(4/4)] + 5/14*[-3/5log2(3/5) – 2/5*log2(2/5)] = 0.694
• Ent(温度) = 0.911
• Ent(湿度) = 0.789
• Ent(风速) = 0.892

（3）第三步：计算信息增益

• Gain(天气) = Ent(D) - Ent(天气) = 0.246
• Gain(温度) = Ent(D) - Ent(温度) = 0.029
• Gain(湿度) = Ent(D) - Ent(湿度) = 0.150
• Gain(风速) = Ent(D) - Ent(风速) = 0.048

（4）第四步：计算特征(属性)分裂信息度量

• IV(天气) = -5/14*log2(5/14) – 4/14*log2(4/14) – 5/14*log2(5/14) = 1.577
• IV(温度) = 1.556
• IV(湿度) = 1.000
• IV(风速) = 0.985

（5）第五步：计算信息增益率

• Gain_ratio(天气) = 0.246 / 1.577 = 0.155
• Gain_ratio(温度) = 0.0187
• Gain_ratio(湿度) = 0.151
• Gain_ratio(风速) = 0.048

可以看到，天气的信息增益率最高，选择天气为分裂属性。发现分裂了之后，天气是“阴”的条件下，类别是”纯“的，所以把它定义为叶子节点，选择不“纯”的结点继续分裂。

我们在ID3和CART中的例子特征值是离散的，即特征值是一个个数值，不是本例中的类别，如果特征是类别的样本，就没有阈值的选择，直接按该特征的类别进行分裂，比如本例中按天气把决策树分裂成晴、阴、雨三个结点。

思考：为什么说信息增益准则对可取值数目较多的特征有所偏好？

就如本例中的天气特征，它的可取值数据为3个：晴、阴、雨，如果天气特征的可取值数目增加到5个，那么按照天气分裂后的信息熵就会降低的更多，它的信息增益就越大，因为天气特征的可取值数目越多，分裂的就清晰。如果把天气特征的可取值数目增加到与样本数一样，那么分裂后的信息熵就是0了，所以说信息增益准则对可取值数目较多的特征有所偏好。

思考：为什么说信息增益率对可取值数目较少的特征所有偏好？

还拿本例中的天气特征来说，它的可取值数据为3个：晴、阴、雨，如果天气特征的可取值数目减少到一个，那么天气特征(属性)分裂信息度量就为0了，此时，信息增益率就是无穷大，因此信息增益率对可取值数目较少的特征所有偏好。

各种决策树比较与总结

ID3、CART、C4.5比较
信息增益和信息增益率通常用于离散型的特征划分，ID3和C4.5通常情况下都是多叉树，也就是根据离散特征的取值会将数据分到多个子树中，当然采用信息增益和信息增益率的时候也可以对连续特征进行划分并计算最优点，如上面判断好坏学生的例子。CART树为二叉树，使用基尼指数作为划分准则，对于离散型特征和连续行特征都能很好的处理。
离散型的特征是指：特征是分类，如天气：晴、阴、雨，不是连续的值
连续型的特征是指：特征是一个个值，如分数、身高等，不是分类

决策树的参数和训练方法：

• 决策树的参数：选择的特征及其对应的阈值，还有它的拓扑结构
• 训练方法：就是遍历的方法，用纯度、基尼系数、信息熵、信息增益或信息增益率来表示
• 决策树既可以做分类，也可以做回归，既可以做二分类，也可以做多分类

决策树中的分类器：

如何求解决策树？

求解决策树，实际上就是求解分类器(求解每个特征和阈值)，步骤如下：

1. 设定一个评价分类结果的好坏的准则(信息增益、基尼系数、纯度、信息增益率)
2. 用遍历的方法求解

决策树编程实战

调用sklearn库实现回归决策树

import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn import linear_model# Data set
x = np.array(list(range(1, 11))).reshape(-1, 1)
y = np.array([5.56, 5.70, 5.91, 6.40, 6.80, 7.05, 8.90, 8.70, 9.00, 9.05]).ravel()# Fit regression model
model1 = DecisionTreeRegressor(max_depth=1)
model2 = DecisionTreeRegressor(max_depth=3)
model3 = linear_model.LinearRegression()
model1.fit(x, y)
model2.fit(x, y)
model3.fit(x, y)# Predict
X_test = np.arange(0.0, 10.0, 0.01)[:, np.newaxis]
y_1 = model1.predict(X_test)
y_2 = model2.predict(X_test)
y_3 = model3.predict(X_test)# Plot the results
plt.figure()
plt.scatter(x, y, s=20, edgecolor="black",c="darkorange", label="data")
plt.plot(X_test, y_1, color="cornflowerblue",label="max_depth=1", linewidth=2)
plt.plot(X_test, y_2, color="yellowgreen", label="max_depth=3", linewidth=2)
plt.plot(X_test, y_3, color='red', label='liner regression', linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()

输出

手动实现ID3决策树

#coding:utf-8
import torch
import pdb# 样本的特征，每个样本包含七个特征
feature_space=[[1., 3., 2., 2., 3., 0.,3.], 
[2., 0., 2., 5., 1., 2.,3.], 
[3., 2., 3., 3., 2., 3.,2.], 
[4., 0., 3., 3., 2., 0.,1.], 
[3., 1., 2., 2., 5., 1.,3.], 
[1., 4., 3., 3., 1., 5.,2.], 
[3., 3., 3., 3., 1., 0.,1.], 
[5., 1., 1., 4., 2., 2.,2.], 
[6., 2., 3., 3., 2., 3.,0.], 
[2., 2., 2., 2., 5., 1.,4.]]def get_label(idx):label= idxreturn label# 计算以某个特征某个阈值进行分裂时的信息熵，即条件熵
def cut_by_node(d,value,feature_space,list_need_cut):# 分别存放以某个特征某个阈值分裂后的左右侧样本点right_list=[]left_list=[]for i in list_need_cut:if feature_space[i][d]<=value:right_list.append(i)else:left_list.append(i)left_list_t = list2label(left_list,[0,0,0,0,0,0,0,0,0,0])right_list_t = list2label(right_list,[0,0,0,0,0,0,0,0,0,0])e1=get_emtropy(left_list_t) e2=get_emtropy(right_list_t) n1 = float(len(left_list))n2 = float(len(right_list))e = e1*n1/(n2+n1) + e2*n2/(n1+n2)return e,right_list,left_list# 将分到样本点转为one-hot各式，方便计算信息熵
def list2label(list_need_label,list_label):for i in list_need_label:label=get_label(i)list_label[label]+=1return list_labeldef get_emtropy(class_list):E = 0sumv = float(sum(class_list))if sumv == 0:sumv =0.000000000001for cl in class_list:if cl==0:cl=0.00000000001p = torch.tensor(float(cl/sumv))# log以2为底E += -1.0 * p*torch.log(p)/torch.log(torch.tensor(2.))return E.item()

def get_node(complate,d,list_need_cut):# 初始时的信息熵，设为最大(根节点计算之前的信息熵)e = 10000000# node 代表以那个维度的那个特征值进行分裂node=[]# list_select:树分裂好的一个个结点序列，不包含已经分类好可以识别的结点list_select=[]# 存放可以识别的结点complate_select=[]# 0~8就是选择的阈值for value in range(0,8):complate_tmp=[]etmp=0list_select_tmp=[]# 子序列总的长度sumv=0.000000001# 要进行分裂的所有结点序列for lnc in list_need_cut:# 计算条件熵，返回熵、左侧结点的样本点，右侧结点的样本点etmptmp,r_list,l_list=cut_by_node(d,value,feature_space,lnc)# 这行代码和etmp/sumv 就是求分裂后的总熵，就是那个pl*H1+pr*H2的公式etmp+=etmptmp*len(lnc)sumv+=float(len(lnc))# 存放可以识别的结点if len(r_list)>1:list_select_tmp.append(r_list)if len(l_list)>1:list_select_tmp.append(l_list)if len(r_list)==1:complate_tmp.append(r_list)if len(l_list)==1:complate_tmp.append(l_list)# print('子序列child:以每个样本的第{}个特征，特征值大小为{}划分{}子序列，得到的熵为{}'.format(d,value,lnc,etmptmp)) etmp = etmp/sumvsumv=0# print('总序列All：以每个样本的第{}个特征，特征值大小为{}划分{}序列，得到的总熵为{}'.format(d,value,list_need_cut,etmp)) # 得到第n个特征以某一阈值分裂后的最小信息熵，及此时分裂后序列if etmp<e:e=etmpnode=[d,value]list_select=list_select_tmpcomplate_select=complate_tmpfor ll in complate_select:complate.append(ll)return node,list_select,complate

import pdb
def get_tree():
# pdb.set_trace()# 10个样本：0, 1, 2, 3, 4, 5, 6, 7, 8, 9，注意是这里是二维数组## 二维数组里刚开始只有一个序列，即初始时只有一个根节点all_list=[[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]] # complate的含义是：比如树的某个结点只有一个样本，那么存放到complate中## 即complate存放的是已经分类好的可以识别的结点complate=[]# 遍历样本的7个特征，这个序列就是遍历的先后顺序## d 首先遍历每个样本的第3个特征，把分类的结果返回for d in [3,4,2,5,0,1,6]:# node 代表以那个维度的那个特征值进行分裂# all_list:树分裂好的一个个结点序列，不包含已经分类好可以识别的结点node,all_list,complate=get_node(complate,d,all_list)print("node=%s,complate=%s,all_list=%s"%(node,complate,all_list))if __name__=="__main__":get_tree()

输出：

使用sklearn库回归决策树预测boston房价

decision_sklearn_tree_regressor_boston

使用sklearn库分类决策树对iris分类

decision_sklearn_tree_classify_iris

参考文档
信息增益、信息增益比、基尼指数的比较
华校专的决策树
机器学习（二）-信息熵，条件熵，信息增益，信息增益比，基尼系数