在分类中,首先对于Logistic回归:
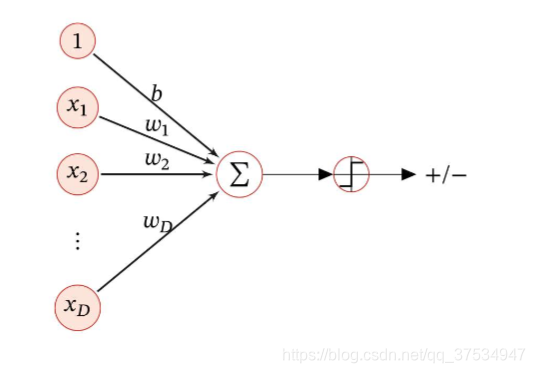
从上图可以看出,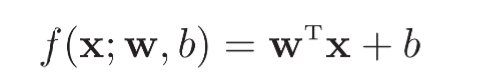
很明显,其输出f(x;wb)主要是一些连续的实数,可以用于线性回归,但是对于分类问题无法进行直接进行分类预测,这里需要引入非线性的决策函数g(.)—这里我认为就是激活函数,使其输出从连续的实数转换到一些离散的标签。
对于激活函数,可分为一下:

其中tanh、relu、以及leaky relu激活函数相比sigmoid和softmax不适用与分类,其主要的作用以及差别见链接--------待
这里主要来介绍sigmoid和softmax激活函数,而sigmoid主要用于二分类,softmax激活函数主要用于多分类。
(一)sigmoid/logistic
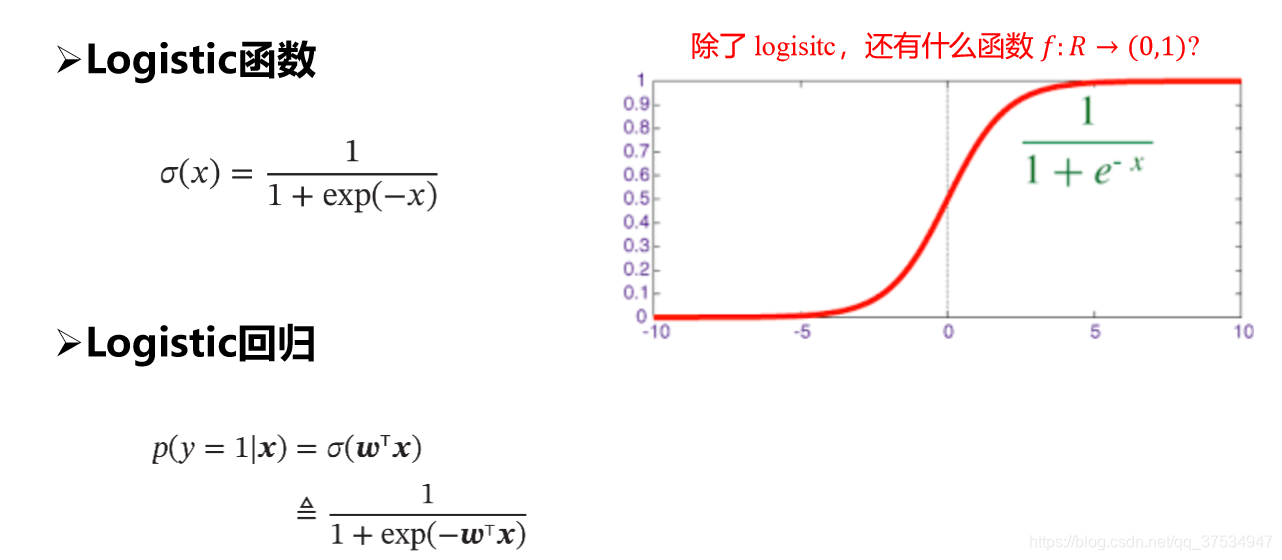
可以看出其把从实数区间的值挤压到了(0,1)概率之间,这样可以认为: 这里选取0.5作为阈值可以用于二分类。
这里选取0.5作为阈值可以用于二分类。
注:这里简单介绍一下二分类:
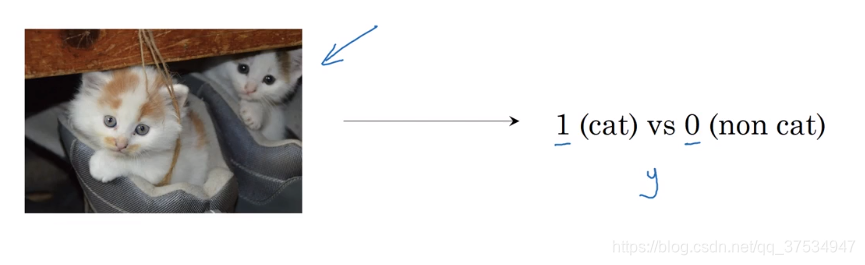
如:上图就是判断一张图片是否是猫,答案为:1猫 、0不是猫。
(二)softmax

对于最后的输出经过softmax函数得到的值其和是为1的。
(三)针对上面的激活函数,选择损失函数:

注:y帽 是预测的值。
这里只列取了两个,对于分类,主要利用第二个—交叉熵损失函数,因为对于第一个平方和损失函数,会导致L是非凸的函数,会有多个极限值。
1)sigmoid激活函数对应的交叉熵损失函数
if y=1,L(y帽,y) = -log(y帽),为了使L较小,希望y帽较大
if y=0,L(y帽,y) = log(1-(y帽)),同理为了使L较小,希望y帽较小.
可以看出对于不同的真值1/0,其y帽对应变大和变小,符合我们的要求。
对于所有样本,即对所有的m个样本进行L平均求和即可。
分析其公式的由来:
因为我们在前面设置了预测的y帽的概率即下面的公式:
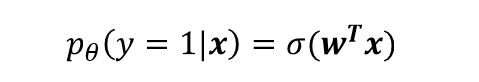
然后,对应我们认为y帽是真值y=1的概率,而1-y帽是真值y=0的概率,然后从下面的推导中(合并p(y|x),取log对数等),可以得出L为上面的公式。
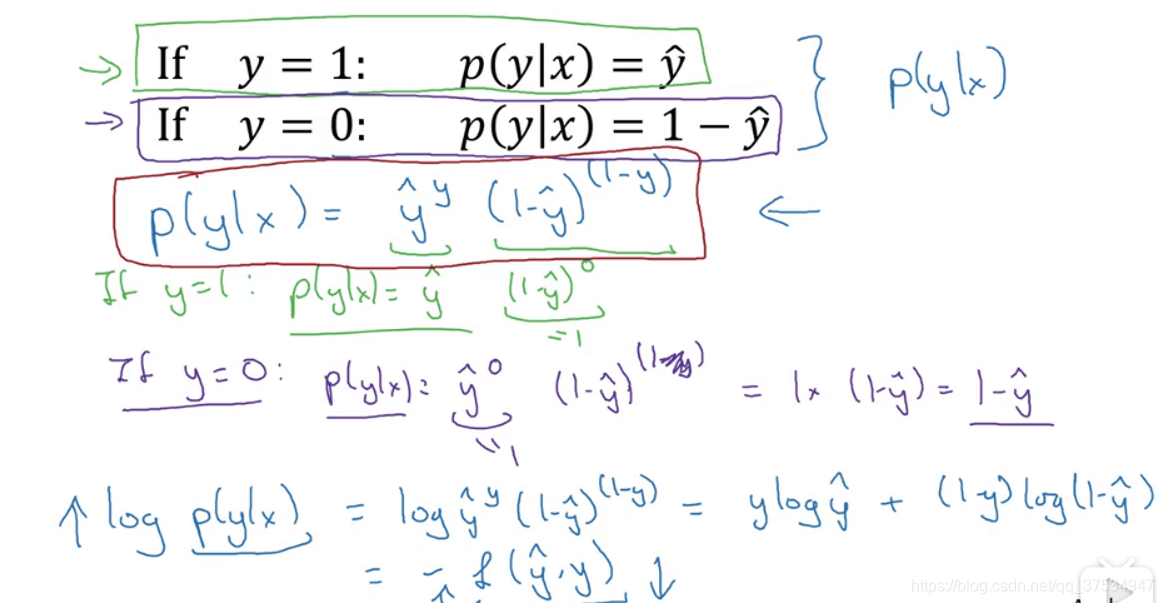
注:这部分对于上面的p(y=1|x)=sigmoid(x)的由来不是太清楚,可能就是这样定义的吧,然后后面都以此为基础,然后推导出来的。
参考:https://www.bilibili.com/video/BV1w741147Ac?p=9
2)softmax激活函数的交叉熵损失函数
引:其实对于多分类(C>2个类别)问题可以转换为二分类问题
第一种将其转换为1对其余的方式,需要c个判别函数
第二种将其转换为1对1的方式,需要c(c-1)/2的判别函数
第三种,argmax方式,是1对其余的改进方式,不是明确的一对其余,而是比较了其大小。
上面几种或多或少存在些问题,可以自己查一查,并且不常用吧!!
第四种:softmax激活函数。
主要见下面的softmax的交叉熵损失函数:

其输出有c个值,不像二分类只有一个值,这c个值分别代表每个类别的预测概率,所以可以看到softmax最后的风险函数只有一个分支。最后的loss损失函数:
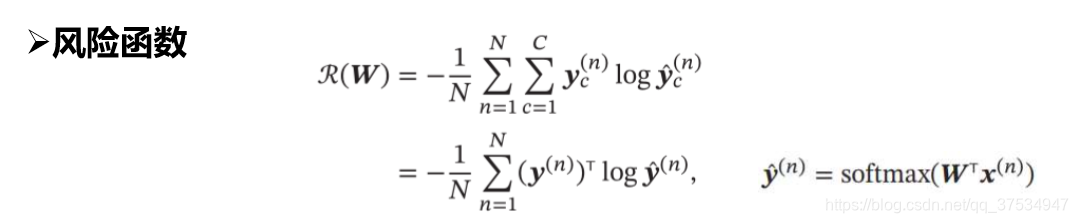
分析:
其公式本质应该是(对于一个样本):
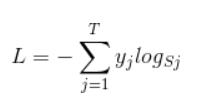
但是,因为其利用了one-hot编码方式,在相乘的时候,只有真实标签对应的logs才会保留,所以可以简化为:
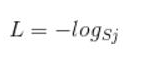
为什么这种方式符合咱们的条件,可以看下面的例子:
假设一个5分类问题,然后一个样本I的标签y=[0,0,0,1,0],
也就是说样本I的真实标签是4,假设模型预测的结果概率(softmax的输出)p=[0.1,0.15,0.05,0.6,0.1],可以看出这个预测是对的,那么对应的损失L=-log(0.6),也就是当这个样本经过这样的网络参数产生这样的预测p时,它的损失是-log(0.6)。那么假设p=[0.15,0.2,0.4,0.1,0.15],这个预测结果就很离谱了,因为真实标签是4,而你觉得这个样本是4的概率只有0.1(远不如其他概率高,如果是在测试阶段,那么模型就会预测该样本属于类别3),对应损失L=-log(0.1)。那么假设p=[0.05,0.15,0.4,0.3,0.1],这个预测结果虽然也错了,但是没有前面那个那么离谱,对应的损失L=-log(0.3)。我们知道log函数在输入小于1的时候是个负数,而且log函数是递增函数,所以-log(0.6) < -log(0.3) < -log(0.1)。简单讲就是你预测错比预测对的损失要大,预测错得离谱比预测错得轻微的损失要大。
例子参考:https://blog.csdn.net/u014380165/article/details/77284921
总结比较:

附:
对于交叉熵以及熵 的各个概念的理解,可以参考下面的图片:


目前我的理解能力有限,从其本质出发比较吃力,有能力的同学可以看一下,如果有自己的理解,可以给我讲讲。
补充:sigmoid激活函数y的导数是y(1-y);tanh激活函数y的导数是是1-y的平方。