支持向量机：PRML:SparseKernelMachine_综合

SparseKernelMachine

前言

这章主要在讲SVM，花费了很多时间，文中大量参考了各种国内外博客，因为英文水平，国外的参考较少仍，同时加入了我许多理解，但是仍有许多数学需要学习，肯定存在问题，希望指出，之后研究生阶段将进一步修改。

SVM

svm有三宝，间隔对偶核技巧。svm相当于一个判别函数，是纯粹的判别模型，寻找一个超平面分割数据点。通俗来讲，它是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，即支持向量机的学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。

hard-margin

我们将从问题提出到解决的①②③④⑤来理解。

前置知识：函数间隔，几何间隔的介绍

观察如下图：

上图中 $x_0$ 是 $x$ 在超平面上的投影， $ω\omega$ 是超平面 $ωTx+b=0\omega^Tx+b=0$ 的法向量，可以得到：
$x?x0=γω∥ω∥x-x_0=\gamma \frac{\omega}{\Vert \omega\Vert}$
也就是说：
$γ=ωTx+b∥ω∥\gamma = \frac{\omega^Tx+b}{\Vert \omega \Vert}$
取消符号我们得到几何间隔为：
$γ~=∥ωTx+b∥∥ω∥\tilde{\gamma} = \frac{\Vert \omega^Tx+b \Vert}{ \Vert \omega \Vert}$
函数间隔为：
$γ^=∥ωTx+b∥\hat{\gamma} = \Vert \omega^Tx+b \Vert$

可以理解为函数间隔是几何间隔没有除以||w||的表达，几何间隔是函数间隔归一化的结果。
我们可以知道每个点到确定的超平面的几何间隔是确定的，而每个点到确定的超平面的函数间隔却又无数个，因为 $ωTx+b=0\omega^Tx+b=0$ 和 $10ωTx+10b=010\omega^Tx+10b=0$ 是相同的超平面。但是当一个点到超平面的函数间隔确定了，那么其余所有点也就确定了。

前置知识：QP二次规划问题

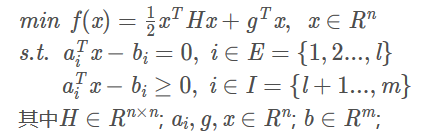
在这里插入图片描述
若 $H$ 为正定矩阵，求解 $x$ ,则问题称为严格的凸二次规划问题。二次规划计算机帮助可以不用手工求解，复杂度主要由求解的 $x$ 决定。

前置知识：强弱对偶的介绍以及KKT条件

KKT条件
我们定义一个优化问题
$min?xf(x)s.t.gi(x)≤0,i=1,?,khj(x)=0,j=1,?,l\min_{x}f(x)\\ s.t. g_i(x)\leq0,i=1, \cdots,k\\ h_j(x)=0,j=1, \cdots,l$
KKT是干嘛用的？原来KKT是优化问题取得极值的必要条件。如果一个优化问题满足一定约束，我们可以使用KKT求解极值。可以理解KKT是求解极值的一种方法。优化问题满足哪些约束可以使用KKT来求极值呢？这些约束规范在wiki可以详细的看到。这里我们只需要知道的SVM是一个凸二次规划问题，所以肯定可以KKT用来求极值。KKT的具体形式如下：
${原始问题可行:gi(x)?0,i=1,2...khj(x)=0,j=1,2...l对偶问题可行:αi?0,i=1,2...k互补松弛:αigi(x)=0拉格朗日平稳性:?xL(x,α,β)=0\begin{cases} 原始问题可行: & g_i(x) \leqslant 0,i=1,2...k \;\\ &{h_{j}(x) = 0},j=1,2...l \\ 对偶问题可行: & \alpha_i \geqslant 0,i=1,2...k \\ 互补松弛: & \alpha_i g_i(x) = 0 \\ 拉格朗日平稳性: & \nabla_{x}\mathcal{L}(x, \boldsymbol{\alpha}, \boldsymbol{\beta}) = 0 \end{cases}$
如何理解KKT条件能求极值。
如果只有等式约束，就是普通的拉格朗日乘数法。那么对于不等式约束，我们的极值可能存在情况有两种。若最优点 $下x^?$ 在区域内 (下左图， $g_i(x)<0$ ) ，则不等式约束并没有起到”约束的作用“，不等式约束等价于 $αi=0\alpha_i = 0$ 。若最优点 $x^?$ 在区域边界上 (下右图， $g_i(x)=0$ ),不等式约束这等价于一个 $αi>0\alpha_i > 0$ 的等式条件。综合两种可能有
${αi?0,i=1,2...kαigi(x)=0,i=1,2...k\begin{cases} \alpha_i \geqslant 0,i=1,2...k \\ \alpha_i g_i(x) = 0,i=1,2...k \\ \end{cases}$
原问题与原问题Ⅱ定义
对于如下优化问题，我们称之为原问题。原问题的目标函数是关于 $x$ 的。
$min?xf(x)s.t.gi(x)≤0,i=1,?,khj(x)=0,j=1,?,l\min_{x}f(x)\\ s.t. g_i(x)\leq0,i=1, \cdots,k\\ h_j(x)=0,j=1, \cdots,l$
利用拉格朗日乘数法，我们得到如下拉格朗日函数，这步是为了得到原问题的等价形式。
$L(x,α,β)=f(x)+∑i=1kαigi(x)+∑j=1lβjhj(x)αi≥0,i=1,?,k\mathcal{L}(x, \boldsymbol{\alpha},\boldsymbol{\beta}) = f(x)+\sum^k_{i=1}\alpha_ig_i(x)+\sum^l_{j=1}\beta_jh_j(x)\\ \alpha_i\geq0,i=1, \cdots,k$
原问题等价于如下形式的优化问题，我们称之为原问题Ⅱ：
$min?xmax?α,βL(x,α,β)αi≥0,i=1,?,k\min _{x} \max _{\boldsymbol{\alpha}, \boldsymbol{\beta}} \mathcal{L}(x, \boldsymbol{\alpha}, \boldsymbol{\beta}) \\ \alpha_i\geq0,i=1, \cdots,k$
从原问题Ⅱ到原问题的推导
等价的原因我们从原问题Ⅱ的角度出发，推导出原问题。原问题Ⅱ可以等价于如下形式。我们暂且称之为中间形式。
$min?x(f(x)+max?α,β(∑i=1mαigi(x)+∑j=1nβjhj(x)))αi≥0,i=1,?,k\min _{x}\left(f(x)+\max _{\boldsymbol{\alpha}, \boldsymbol{\beta}}\left(\sum_{i=1}^{m} \alpha_{i} g_{i}(x)+\sum_{j=1}^{n} \beta_{j} h_{j}(x)\right)\right) \\ \alpha_i\geq0,i=1, \cdots,k$
我们定义如下两个概念。
$x$ 满足约束: $gi(x)≤0,i=1,?,k并且hj(x)=0,j=1,?,lg_i(x)\leq0,i=1, \cdots,k并且h_j(x)=0,j=1, \cdots,l$
$x$ 不满足约束:存在 $gi(x)>0,或者hj(x)≠0g_i(x)>0,或者h_j(x)\neq0$
那么在 $αi≥0,i=1,?,k\alpha_i\geq0,i=1, \cdots,k$ 前提下，从中间形式，我们可以得到如下推论:
$min?x(f(x)+{0,若x满足约束∞,若x不满足约束)\min_{x}\left(f(x)+\left\{\begin{array}{l}{0}\,, & 若 x \,满足约束 \\ {\infty}\,, & 若 x \,不满足约束\end{array}\right.\right)$
由此推论我们可以将将中间形式等价于原问题：
$min?xf(x)s.t.gi(x)≤0,i=1,?,khj(x)=0,j=1,?,l\min_{x}f(x)\\ s.t. g_i(x)\leq0,i=1, \cdots,k\\ h_j(x)=0,j=1, \cdots,l$
对偶问题
我们可以得到对偶问题如下，对偶问题的目标函数是关于 $α,β\alpha,\beta$ 的。：
$max?α,βmin?xL(x,α,β)αi≥0,i=1,?,k\max_{\boldsymbol{\alpha}, \boldsymbol{\beta}}\min_{x}\mathcal{L}(x,\boldsymbol{\alpha}, \boldsymbol{\beta})\\ \alpha_i\geq0,i=1, \cdots,k$
当强对偶性条件满足，原问题的最优解等同于对偶问题的最优解。
当原问题满足slater条件，强对偶成立。
slater条件就是，首先是一个凸优化问题（ $f, g$ 为凸函数， $h$ 是仿射函数），其次至少存在绝对一个绝对可行点（什么叫绝对可行点，就是存在一个点 $x^*$ ,满足 $g_i(x*)<0,i=0,1...k$ 。放松的slater条件是， $g_i(x),i=0,1...k$ 当有 $m$ 个仿射函数，那么只需要存在一个可行点使得剩余的 $k ? m$ 个不等式严格成立。我们的SVM是凸二次规划，满足slater条件。
对偶间隔的几何理解
我们假设一个简单的优化问题。原问题：
$min?xf(x)s.t.m(x)≤0\min_{x}f(x)\\ s.t. \quad m(x)\leq0$
那么对偶问题为：
$max?αmin?xL(x,λ)λ≥0\max _{\alpha} \min _{x} \mathcal{L}(x,\lambda) \\ \lambda\geq0$
我们令 $(u,t)\in \mathcal{G}$
$p?=inf?{t∣(u,t)∈G,u≤0}g(λ)=inf?{t+λu∣(u,t)∈G}d?=sup?{g(λ)∣λ≥0}p^{\ast}=\inf\lbrace t\mid (u,t)\in \mathcal{G}, u\leq0\}\\ g(\lambda)= \inf \{t+\lambda u\mid (u,t)\in \mathcal{G}\}\\ d^{\ast}= \sup\{g(\lambda) \mid \lambda\geq0\}$

①核心问题

给定一个数据集 ${x_i\}_{i}^{m}$ ， $xi?Rpx_i\epsilon \mathbb{R}^{p}$ ， $yi?{+1,?1}y_i\epsilon\{+1,-1\}$ 。数据集中的数据完全可分。我们想要找到一个超平面来完全分隔开数据，这个超平面决定了我们的模型 $margin(ω,b)margin(\omega,b)$ ，也就是最大分类器模型。假如我们已经找到了这个超平面，我们将满足如下条件的数据称为支持向量，其实就是距离超平面最近的点。
$arg?min?x∥ωTx+b∥∥ω∥\argmin_{x} \quad \frac{\Vert \omega^Tx+b \Vert}{\Vert \omega \Vert}$
但是我们还没有找到超平面，我们寻找超平面的原则也很朴素，就是找到令支持向量到超平面的距离最大的超平面。也就是满足如下式子的超平面，超平面就是 $(ω,b)(\omega,b)$ 。
$max?ω,bmin?xi,i=1,2..m∥ωTxi+b∥∥ω∥\max_{\omega,b} \min_{x_i,i=1,2..m} \quad \frac{\Vert \omega^Tx_i+b \Vert}{\Vert \omega \Vert}$
因为存在最大化最小化，我们可以假设一个不变来思考，方便理解。还需要满足我们开始提出的数据完全可分。
$yi(ωTxi+b)?0,i=1,2,...,m\quad y_i(\omega^T x_i + b) \geqslant 0 ,\quad i=1,2,...,m$
这样我们得出了最初的优化目标如下,此时记得我们最终需要的是模型 $margin(ω,b)margin(\omega,b)$ 中的参数 $(ω,b)(\omega,b)$ ，我们通过求解优化目标来得到所需参数：
${max?ω,bmin?xi,i=1,2..m∥ωTxi+b∥∥ω∥s.t.yi(ωTxi+b)?0,i=1,2,...,m\left \{ \begin{matrix} \max_{\omega,b} \min_{x_i,i=1,2..m} \quad \frac{\Vert \omega^Tx_i+b \Vert}{\Vert \omega \Vert} \\ s.t. \quad y_i(\omega^T x_i + b) \geqslant 0 ,\quad i=1,2,...,m \end{matrix} \right.$
接下来，由于数据集数据线性可分，我们可以将分子的绝对值替换，化简一下一下优化目标。
${max?ω,bmin?xi,i=1,2..myi(ωTxi+b)∥ω∥s.t.yi(ωTxi+b)?0,i=1,2,...,m\left \{ \begin{matrix} \max_{\omega,b} \min_{x_i,i=1,2..m} \quad \frac{y_i ( \omega^Tx_i+b )}{\Vert \omega \Vert} \\ s.t. \quad y_i(\omega^T x_i + b) \geqslant 0 ,\quad i=1,2,...,m \end{matrix} \right.$
接下来由于分子是函数间隔，函数间隔可以缩放，我们将支持向量的函数间隔设定为1。也就是
$min?xi,i=1,2..myi(ωTxi+b)=1\min_{x_i,i=1,2..m} y_i ( \omega^Tx_i+b ) = 1$

那么优化目标可以进一步化简为：
${max?ω,b1∥ω∥s.t.yi(ωTxi+b)?1,i=1,2,...,m\left \{ \begin{matrix} \max_{\omega,b} \quad \frac{1}{\Vert \omega \Vert} \\ s.t. \quad y_i(\omega^T x_i + b) \geqslant 1 ,\quad i=1,2,...,m \end{matrix} \right.$
我们将优化目标再一次化简, $12\frac{1}{2}$ 只是为了方便计算添加。
${min?ω,b12ωTωs.t.1?yi(ωTxi+b)?0,i=1,2,...,m\left \{ \begin{matrix} \min_{\omega,b} \quad \frac{1}{2} \omega^T\omega \\ s.t. \quad 1-y_i(\omega^T x_i + b) \leqslant 0 ,\quad i=1,2,...,m \end{matrix} \right.$
如果数据集小，且数据的维度p低，那么此时就是一个简单的二次规划问题（QP）。

但是在现实中有两大难题，1个是数据的维度也可能很高，同时线性不可分，1个是数据集太大，我们需要更好的解决方法。由于这个问题的特殊结构，还可以通过拉格朗日对偶性（Lagrange Duality）变换到对偶变量 (dual variable) 的优化问题，即通过求解与原问题等价的对偶问题（dual problem）得到原始问题的最优解，这就是线性可分条件下支持向量机的对偶算法，这样做的优点在于：一者对偶问题往往更容易求解，解决数据的维度高问题；二者可以自然的引入核函数，进而推广到非线性分类问题。对偶形式可以用二次规划问题求解，但是受到数据集大小的限制。我们最后将引入SMO算法，解决数据集太大求解对偶算法的困难的问题。

②问题的拉格朗日表达与其对偶形式

接下来我们使用拉格朗日乘数法将带约束的优化目标化转变为不带约束的优化目标。我们使用 $α\alpha$ 替代 $α1...αm\alpha_1...\alpha_m$ ，拉格朗日函数是则表达为：
$L(ω,b,α)=12∥ω∥2+∑i=1mαi[1?yi(ωTxi+b)]L(\omega,b,\alpha)=\frac{1}{2}\|\omega\|^2 + \sum_{i=1}^m\alpha_i\Big[1-y_i(\omega^Tx_i+b)\Big]$
我们可以写出原问题的对偶问题：
${max?αmin?ω,bL(ω,b,α)s.t.αi?0,i=1,2,...,m\left \{ \begin{matrix} \max_{\alpha} \min_{\omega,b} L(\omega,b,\alpha) \\ s.t. \alpha_i \geqslant 0 ,\quad i=1,2,...,m \end{matrix} \right.$

目标是二次的，约束是线性的，这属于凸二次优化问题，那么满足强对偶，满足强对偶意味着满足KKT条件。

③求解 $ω,b\omega,b$

现在我们把 $α\alpha$ 看做常数，先求解 $min?ω,bL(ω,b,α)\min_{\omega,b} L(\omega,b,\alpha)$ 得到 $ω,b\omega,b$ 。

$?L(ω,b,α)?ω=ω?∑i=1mαiyixi=0\frac{\partial L(\omega,b,\alpha)}{\partial \omega}=\omega-\sum_{i=1}^{m}\alpha_iy_ix_i=0$
$?L(ω,b,α)?b=∑i=1mαiyi=0\frac{\partial L(\omega,b,\alpha)}{\partial b}=\sum_{i=1}^{m}\alpha_iy_i=0$

通过上面的式子，这时候 $ω\omega$ 得到了解，由下面的KKT条件得知其实当 $x_i$ 不是支持向量，那么 $αi=0\alpha_i=0$ ，所以 $ω\omega$ 仅由支持向量决定。
$ω?=∑i=1mαiyixi\omega^*=\sum_{i=1}^{m}\alpha_iy_ix_i$
那么 $b$ 要通过KKT条件中的松弛互补条件获得。首先我们看一下现在满足的KKT条件如下。
${?L(ω,b,α)?ω=0?L(ω,b,α)?b=0αi?0,i=1,2,...,m1?yi(ωTxi+b)?0,i=1,2,...,mαi[yi(ωTxi+b)?1]=0,i=1,2,...,m\left \{ \begin{matrix} \frac{\partial L(\omega,b,\alpha)}{\partial \omega}=0 \\ \frac{\partial L(\omega,b,\alpha)}{\partial b}=0 \\ \alpha_i\geqslant 0,\quad i=1,2,...,m \\ 1-y_i(\omega^Tx_i+b)\leqslant 0,\quad i=1,2,...,m \\ \alpha_i[y_i(\omega^Tx_i+b)-1]=0,\quad i=1,2,...,m \end{matrix} \right.$
根据KKT松弛互补条件也就是上面最后条，如果我们知道 ${αi}i=1m\{\alpha_i\}_{i=1}^m$ 的值,任取 $αk>0\alpha_k>0$ 同时取得对应的 $x_k,y_k$ ,那么 $yk(ω?Txk+b)?1=0y_k(\omega^{*T}x_k+b)-1=0$ ,也就意味着 $x_k$ 为支持向量。已知：
$ω?=∑i=1mαiyixi\omega^*=\sum_{i=1}^{m}\alpha_iy_ix_i$
那么 $b^*$ 也被求解得到：
$b?=yk?ω?Txk=yk?∑i=1mαiyixiTxkb^*=y_k-\omega^{*T}x_k=y_k-\sum_{i=1}^{m}\alpha_iy_ix_i^Tx_k$
模型也被求解得到： $margin(ω,b)=sign(ω?Tx+b?)margin(\omega,b)=sign(\omega^{*T}x+b^*)$

但是我们并不知道 ${αi}i=1m\{\alpha_i\}_{i=1}^m$ ，我们需要求解 ${αi}i=1m\{\alpha_i\}_{i=1}^m$ 之后才能得到 $b?，ω?b^*，\omega^*$

④求解 $α\alpha$

虽然在求得 ${αi}i=1m\{\alpha_i\}_{i=1}^m$ 前，无法得到 $b?，ω?b^*，\omega^*$ 。但我们知道如下结论:
$?L(ω,b,α)?ω=ω?∑i=1mαiyixi=0\frac{\partial L(\omega,b,\alpha)}{\partial \omega}=\omega-\sum_{i=1}^{m}\alpha_iy_ix_i=0$
$?L(ω,b,α)?b=∑i=1mαiyi=0\frac{\partial L(\omega,b,\alpha)}{\partial b}=\sum_{i=1}^{m}\alpha_iy_i=0$
我们把这两个值代入 $L(ω,b,α)L(\omega,b,\alpha)$ ，求得 $min?ω,bL(ω,b,α)\min_{\omega,b}L(\omega,b,\alpha)$
$min?ω,bL(ω,b,α)=12∥ω∥2+∑i=1mαi[1?yi(ωTxi+b)]=12∥∑i=1mαiyixi∥2+∑i=1mαi?ωT∑i=1mαiyixi=∑i=1mαi+12ωT∑i=1mαiyixi?ωT∑i=1mαiyixi=∑i=1mαi?(∑i=1mαiyixiT)(∑i=1mαiyixi)=∑i=1mαi?∑i=1m∑j=1mαiαjyiyjxiTxj\min_{\omega,b}L(\omega,b,\alpha)=\frac{1}{2}\|\omega\|^2 + \sum_{i=1}^m\alpha_i\Big[1-y_i(\omega^Tx_i+b)\Big] \\ = \frac{1}{2}\left\| \sum_{i=1}^{m}\alpha_iy_ix_i \right\|^2 + \sum_{i=1}^{m}\alpha_i - \omega^T\sum_{i=1}^{m}\alpha_iy_ix_i \\ =\sum_{i=1}^{m}\alpha_i + \frac{1}{2}\omega^T\sum_{i=1}^{m}\alpha_iy_ix_i- \omega^T\sum_{i=1}^{m}\alpha_iy_ix_i \\ =\sum_{i=1}^{m}\alpha_i - \left(\sum_{i=1}^{m}\alpha_iy_ix_i^T\right)\left(\sum_{i=1}^{m}\alpha_iy_ix_i\right) \\ =\sum_{i=1}^{m}\alpha_i - \sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_jx_i^Tx_j$
最终得
$min?ω,bL(ω,b,α)=∑i=1mαi?∑i=1m∑j=1mαiαjyiyjxiTxj\min_{\omega,b}L(\omega,b,\alpha) =\sum_{i=1}^{m}\alpha_i - \sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_jx_i^Tx_j$

于是我们的优化目标转变为如下，求解的变量为 $α\alpha$ 。
${max?α∑i=1mαi?∑i=1m∑j=1mαiαjyiyjxiTxjs.t.∑i=1mαiyi=0αi?0,i=1,2,...,m\left \{ \begin{matrix} \max_{\alpha} \quad \sum_{i=1}^{m}\alpha_i - \sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_jx_i^Tx_j \\ s.t. \sum_{i=1}^{m}\alpha_iy_i=0 \\ \alpha_i \geqslant 0,\quad i=1,2,...,m \end{matrix} \right.$
这时候我们可以利用二次规划求解 $α\alpha$ ，这时候的二次规划问题已经一定程度解决了原数据维度大的问题，但是数据非线性需要引入核函数来解决，优化目标转为如下：
${max?α∑i=1mαi?∑i=1m∑j=1mαiαjyiyjK(xi,xj)s.t.∑i=1mαiyi=0αi?0,i=1,2,...,m\left \{ \begin{matrix} \max_{\alpha} \quad \sum_{i=1}^{m}\alpha_i - \sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_jK(x_i,x_j) \\ s.t. \sum_{i=1}^{m}\alpha_iy_i=0 \\ \alpha_i \geqslant 0,\quad i=1,2,...,m \end{matrix} \right.$

另外此时二次规划复杂度主要是由数据集大小决定，如果数据集太大我们需要更好的解决方法，SMO算法。

⑤SMO算法（求解 $α\alpha$ 另外一种算法）

SMO是一种启发式算法，其特点是不断地将原二次规划问题分解为只有两个变量的二次规划子问题，并对子问题进行解析求解，直到所有变量满足KKT条件为。http://cs229.stanford.edu/notes2019fall/cs229-notes3.pdf，https://blog.csdn.net/ACM_hades/article/details/90701030解答较为清楚。

我们基于soft-margin算法来表达SMO算法，首先介绍SMO算法的流程,之后详细介绍过程：

随机初始化 ${αiold}i=1m，bold=0\{\alpha_i^{old}\}_{i=1}^{m}，b^{old}=0$ ，那么可以计算 ${E_i^{old}\}_{i=1}^{m}$
按照指定方法选定 $α1old，α2old\alpha_1^{old}，\alpha_2^{old}$
计算新的 $α2new\alpha_2^{new}$ ，
$α2new,unclip=α2old+y2(E1old?E2old)K11+K22?2K12α2new={Hα2new,unclip>Hα2new,unclipL≤α2new,unclip≤HLα2new,unclip<L\alpha_2^{new,unclip} = \alpha_2^{old} + \frac{y_2(E_1^{old}-E_2^{old})}{K_{11} +K_{22}-2K_{12}} \\ \alpha_2^{new}= \begin{cases} H& { \alpha_2^{new,unclip} > H} \\ \alpha_2^{new,unclip}& {L \leq \alpha_2^{new,unclip} \leq H}\\ L& {\alpha_2^{new,unclip} < L} \end{cases}$
计算新的 $α1new\alpha_1^{new}$ ， $α1new=α1old+y1y2(α2old?α2new)\alpha_1^{new} = \alpha_1^{old} +y_1y_2(\alpha_2^{old}-\alpha_2^{new})$
利用 ${α1new,α2new,αiold}i=3m\{\alpha_1^{new},\alpha_2^{new},\alpha_i^{old}\}_{i=3}^{m}$ ，更新 $b^{new},\{E_i^{new}\}_{i=1}^{m}$
如果满足条件（1） ${αiend}i=1m\{\alpha_i^{end}\}_{i=1}^{m}$ 不违背KKT条件或者（2）目标函数的增长率小于一个值 $W(αend)?W(αend?1)W(αend?1)<T\frac{W(\alpha^{end})-W(\alpha^{end-1})}{W(\alpha^{end-1})}<T$ 那么停止，否则返回第二步。

接下来我将解释详细的每一步：

随机初始化 ${αiold}i=1m，bold=0\{\alpha_i^{old}\}_{i=1}^{m}，b^{old}=0$ ，那么可以计算 ${E_i^{old}\}_{i=1}^{m}$ 。
这步就是一个初始化操作，为后面计算准备。已知 ${αiold}i=1m，bold=0\{\alpha_i^{old}\}_{i=1}^{m}，b^{old}=0$ ，那么可以计算 ${E_i^{old}\}_{i=1}^{m}$ ， $Eiold=g(xi)?yi=∑j=1myjαjoldK(xi,xj)+bold?yiE_i^{old}=g(x_i)-y_i=\sum\limits_{j=1}^{m}y_j\alpha^{old}_jK(x_i,x_j) +b^{old}-y_i$
按照指定方法选定 $α1old，α2old\alpha_1^{old}，\alpha_2^{old}$ 。
如何选定 $α1old，α2old\alpha_1^{old}，\alpha_2^{old}$ 分两步。第一步是选择第一个点：原则是选取违反KKT条件最严重的样本点。这里的符合KKT条件指下面三个式子(可由下一节soft-margin中KKT条件推出)，优先选择违反 $\alpha_{i} < C \Leftrightarrow y_i (\omega^T x_i+b) =1$ 的点，再选择违反另外两种情况的点。第二步选择第二个点：原则为选择令 $E_1^{old}-E_2^{old}|$ 最大的点。当选定第一个点我们已经知道 $E_1^{old}$ ，那么可以根据 $E_1^{old}-E_2^{old}|$ 寻找第二个点，原因是 $α2new\alpha_2^{new}$ 依赖于 $E_1^{old}-E_2^{old}|$ （下一步会看到），为了让 $α2old\alpha_2^{old}$ 到 $α2new\alpha_2^{new}$ 变化大，所以按照这个规则来选择。
$αi=0?yi(ωTxi+b)≥10<αi<C?yi(ωTxi+b)=1αi=C?yi(ωTxi+b)≤1\alpha_{i} =0 \Leftrightarrow y_i(\omega^T x_i+b) \geq1 \\ 0 < \alpha_{i} < C \Leftrightarrow y_i(\omega^T x_i+b) =1 \\ \alpha_{i}= C\Leftrightarrow y_i(\omega^T x_i+b) \leq 1$
计算新的 $α2new\alpha_2^{new}$ 。再计算新的 $α1new\alpha_1^{new}$ 。
这步是最复杂的。如何得出更新的 $α2new\alpha_2^{new}$ 解释如下：
接下来 $α2new,α1new\alpha_2^{new},\alpha_1^{new}$ 为变量， $α2new?,α1new?\alpha_2^{new*},\alpha_1^{new*}$ 为标量， $α2new?,α1new?\alpha_2^{new*},\alpha_1^{new*}$ 是我这步最终更新的 $α2new,α1new\alpha_2^{new},\alpha_1^{new}$ 的值。
假设选择的两个变量是 $α1new,α2new\alpha^{new}_{1},\alpha^{new}_{2}$ ，其他变量 ${αiold}i=3m\{\alpha^{old}_{i}\}_{i=3}^m$ 是固定的，那么就是标量。于是SMO的最优化问题的子问题经过整理可以写成：
$min?α1new,α2newW(α1new,α2new)=12K11α1new2+12K22α2new2+y1y2K12α1newα2new?(α1new+α2new)+y1α1new∑i=3myiαioldKi1+y2α2∑i=3myiαioldKi2+Bs.t.α1newy1+α2newy2=α1oldy1+α2oldy2=?∑i=3myiαiold=?0≤αinew≤Ci=1,2\;\;\min _{\alpha^{new}_1, \alpha^{new}_2} W(\alpha^{new}_1,\alpha^{new}_2)=\frac{1}{2}K_{11}\alpha_1^{new2} + \frac{1}{2}K_{22}\alpha_2^{new2} \\ +y_1y_2K_{12}\alpha^{new}_1 \alpha^{new}_2 -(\alpha^{new}_1 + \alpha^{new}_2) +y_1\alpha^{new}_1\sum\limits_{i=3}^{m}y_i\alpha^{old}_iK_{i1} + y_2\alpha_2\sum\limits_{i=3}^{m}y_i\alpha^{old}_iK_{i2}+B \\ s.t. \;\;\alpha^{new}_1y_1 + \alpha^{new}_2y_2 =\alpha^{old}_1y_1 + \alpha^{old}_2y_2= -\sum\limits_{i=3}^{m}y_i\alpha^{old}_i = \varsigma \\ 0 \leq \alpha^{new}_i \leq C \;\; i =1,2$
其中 $\varsigma$ 是常数项，前者是与 $α1new,α2new\alpha^{new}_{1},\alpha^{new}_{2}$ 无关项优化项。我们观察到现在目标是优化两个变量，同时存在一个等式约束和一个不等式约束，指导我们的思想就是，先把等式代入消除变量 $α1new\alpha^{new}_{1}$ ，再在不等式可行域上找到我们变量 $α2new\alpha^{new}_{2}$ 的最优解，最后利用等式得到另外一个变量 $α1new\alpha^{new}_{1}$ 的解。
为了让式子看起来更加整洁，我们引入 $vi=∑j=3myjαjoldK(xi,xj)=g(xi)?∑j=12yjαjoldK(xi,xj)?boldv_i = \sum\limits_{j=3}^{m}y_j\alpha^{old}_jK(x_i,x_j) = g(x_i) - \sum\limits_{j=1}^{2}y_j\alpha^{old}_jK(x_i,x_j) -b^{old}$ ,其中有 $g(xi)=∑j=1myjαjoldK(xi,xj)+boldg(x_i)=\sum\limits_{j=1}^{m}y_j\alpha^{old}_jK(x_i,x_j) +b^{old}$ ,那么优化目标写成下式：
$W(α1new,α2new)=12K11α12new+12K22α22new+y1y2K12α1newα2new?(α1new+α2new)+y1α1newv1+y2α2newv2W(\alpha^{new}_1,\alpha^{new}_2) = \frac{1}{2}K_{11}\alpha_1^{2new} + \frac{1}{2}K_{22}\alpha_2^{2 new}+y_1y_2K_{12}\alpha^{new}_1 \alpha^{new}_2 -(\alpha^{new}_1 + \alpha^{new}_2) \\+y_1\alpha^{new}_1v_1 + y_2\alpha^{new}_2v_2$
利用 $α1newy1+α2newy2=?∑i=3myiαiold=?\alpha^{new}_1y_1 + \alpha^{new}_2y_2 = -\sum\limits_{i=3}^{m}y_i\alpha^{old}_i = \varsigma$ 以及 $y_i^2=1$ ,等式关系写成 $α1new=y1(??α2newy2)\alpha^{new}_1 = y_1(\varsigma - \alpha^{new}_2y_2)$ ，代入优化目标消元。整体的优化目标以及约束如下：
$W(α2new)=12K11(??α2newy2)2+12K22α22new+y2K12(??α2newy2)α2new?(??α2newy2)y1?α2new+(??α2newy2)v1+y2α2newv2s.t.0≤α2new≤C0≤y1(??α2newy2)≤CW(\alpha^{new}_2) = \frac{1}{2}K_{11}(\varsigma - \alpha^{new}_2y_2)^2 + \frac{1}{2}K_{22}\alpha_2^{2 new}+y_2K_{12}(\varsigma - \alpha^{new}_2y_2) \alpha^{new}_2 \\ -(\varsigma - \alpha^{new}_2y_2)y_1 - \alpha^{new}_2 +(\varsigma - \alpha^{new}_2y_2)v_1 + y_2\alpha^{new}_2v_2\\ s.t. \;\;0 \leq \alpha^{new}_2 \leq C \\ 0 \leq y_1(\varsigma - \alpha^{new}_2y_2) \leq C$
到这里你一定知道怎么办了，一阶导数等于0来寻找极值点：
$?W?α2new=K11α2new+K22α2new?2K12α2new?K11?y2+K12?y2+y1y2?1?v1y2+y2v2=0\frac{\partial W}{\partial \alpha^{new}_2} = K_{11}\alpha^{new}_2 + K_{22}\alpha^{new}_2 -2K_{12}\alpha^{new}_2 - K_{11}\varsigma y_2 + K_{12}\varsigma y_2 +y_1y_2 -1 -v_1y_2 +y_2v_2 = 0 \\$
那么得到了没经过约束条件的最优值：
$α2new,unclip=α2old+y2(E1old?E2old)K11+K22?2K12\alpha_2^{new,unclip} = \alpha_2^{old} + \frac{y_2(E_1^{old}-E_2^{old})}{K_{11} +K_{22}-2K_{12}}$
接下来我们将根据约束找到 $α2new?\alpha_2^{new*}$ ，一些博客包括课程常用图来解释约束，有更加清晰的理解，这里我想单纯推导来得出结果。
${0≤α2new≤C0≤y1(??α2newy2)≤C\begin{cases} 0 \leq \alpha^{new}_2 \leq C \\ 0 \leq y_1(\varsigma - \alpha^{new}_2y_2) \leq C \end{cases}$
利用 $α1oldy1+α2oldy2=?\alpha_1^{old}y_1 + \alpha_2^{old}y_2 = \varsigma$ 得到
${0≤α2new≤Cy1y2α1old+α2old?Cy1y2≤α2new≤y1y2α1old+α2old\begin{cases} 0 \leq \alpha_2^{new} \leq C \\ \frac{y_1}{y_2}\alpha_1^{old}+\alpha_2^{old}- \frac{C}{y_1y_2} \leq \alpha_2^{new} \leq \frac{y_1}{y2}\alpha_1^{old}+\alpha_2^{old} \end{cases}$
也就是
$max{0,y1y2α1old+α2old?Cy1y2}≤α2new≤min{C,y1y2α1old+α2old}max\{0,\frac{y_1}{y_2}\alpha_1^{old}+\alpha_2^{old}- \frac{C}{y_1y_2}\} \leq \alpha_2^{new} \leq min\{C, \frac{y_1}{y2}\alpha_1^{old}+\alpha_2^{old}\}$
为了表达清楚，令 $L=max{0,y1y2α1old+α2old?Cy1y2},H=min{C,y1y2α1old+α2old}L=max\{0,\frac{y_1}{y_2}\alpha_1^{old}+\alpha_2^{old}- \frac{C}{y_1y_2}\},H=min\{C, \frac{y_1}{y2}\alpha_1^{old}+\alpha_2^{old}\}$ 我们得到了 $α2new?\alpha_2^{new*}$ 。
$α2new?={Hα2new,unc>Hα2new,uncL≤α2new,unc≤HLα2new,unc<L\alpha_2^{new*}= \begin{cases} H& { \alpha_2^{new,unc} > H}\\ \alpha_2^{new,unc}& {L \leq \alpha_2^{new,unc} \leq H}\\ L& {\alpha_2^{new,unc} < L} \end{cases}$
最后利用 $α1oldy1+α2oldy2=α1newy1+α2newy2\alpha_1^{old}y_1 + \alpha_2^{old}y_2 =\alpha_1^{new}y_1 + \alpha_2^{new}y_2$ 可以得到
$α1new?=α1old+y1y2(α2old?α2new?)\alpha_1^{new*} = \alpha_1^{old} +y_1y_2(\alpha_2^{old}-\alpha_2^{new*})$
至此我们将 $α1new,α2new\alpha_1^{new},\alpha_2^{new}$ 更新为 $α1new?,α2new?\alpha_1^{new*},\alpha_2^{new*}$
利用 ${α1new,α2new,αiold}i=3m\{\alpha_1^{new},\alpha_2^{new},\alpha_i^{old}\}_{i=3}^{m}$ ，更新 $b^{new},\{E_i^{new}\}_{i=1}^{m}$ 。
这一步主要是为了下一次的循环做准备，首先是更新 $b^{new}$ ,每当我们更新完一次 $α1new,α2new\alpha_1^{new},\alpha_2^{new}$ ，他们都被约束在了 $\leq \alpha^{new}_i \leq C \;\; i =1,2$ ,同时满足KKT条件，等价于 $yi(ωTxi+b)?1=0i=1,2y_i(\omega^T x_i+b) -1=0 \;\;i=1,2$ 。此时我们得到
$y1?∑i=1mαiyiKi1?b1=0y2?∑i=1mαiyiKi2?b2=0y_1 - \sum\limits_{i=1}^{m}\alpha_iy_iK_{i1} -b_1 = 0 \\ y_2 - \sum\limits_{i=1}^{m}\alpha_iy_iK_{i2} -b_2 = 0$
从而得到：
$b1new=y1?∑i=3mαiyiKi1?α1newy1K11?α2newy2K21b2new=y2?∑i=3mαiyiKi2?α1newy1K12?α2newy2K22b_1^{new} = y_1 - \sum\limits_{i=3}^{m}\alpha_iy_iK_{i1} - \alpha_{1}^{new}y_1K_{11} - \alpha_{2}^{new}y_2K_{21}\\ b_2^{new} = y_2 - \sum\limits_{i=3}^{m}\alpha_iy_iK_{i2} - \alpha_{1}^{new}y_1K_{12} - \alpha_{2}^{new}y_2K_{22}$
进而得到
$E1new=g(x1)?y1=∑i=3mαiyiKi1+α1oldy1K11+α2oldy2K21+bold?y1E2new=g(x2)?y2=∑i=3mαiyiKi2+α1oldy1K12+α2oldy2K22+bold?y2E_1^{new} = g(x_1) - y_1 = \sum\limits_{i=3}^{m}\alpha_iy_iK_{i1} + \alpha_{1}^{old}y_1K_{11} + \alpha_{2}^{old}y_2K_{21} + b^{old} -y_1 \\ E_2^{new} = g(x_2) - y_2 = \sum\limits_{i=3}^{m}\alpha_iy_iK_{i2} + \alpha_{1}^{old}y_1K_{12} + \alpha_{2}^{old}y_2K_{22} + b^{old} -y_2$
一般来说会把 $bnew=12(b1new+b2new)b^{new}=\frac{1}{2}(b_1^{new}+b_2^{new})$
如果满足条件（1） ${αiend}i=1m\{\alpha_i^{end}\}_{i=1}^{m}$ 不违背KKT条件或者（2）目标函数的增长率小于一个值 $W(αend)?W(αend?1)W(αend?1)<T\frac{W(\alpha^{end})-W(\alpha^{end-1})}{W(\alpha^{end-1})}<T$ 那么停止，否则至此我们可以把 $α1new,α2new,bnew,E1new,E2new\alpha_1^{new},\alpha_2^{new},b^{new},E_1^{new},E_2^{new}$ 设置为 $α1old,α2old,bold,E1old,E2old\alpha_1^{old},\alpha_2^{old},b^{old},E_1^{old},E_2^{old}$ ,返回第二步。

soft-margin

我们之前是假设是线性可分的，加入了核技巧对于线性不可分也有了处理能力，但是数据中有噪音，我们强硬的将其隔离是不利于模型的的，因此提出了soft-margin模型。周志华老师是这么说的，每一个数据有一个松弛变量，用以描述该数据不满足约束 $y_i(\omega^T x_i + b) \geq 1 )$ 的情况。所以 $C∑imξiC\sum_{i}^{m} \xi_i$ 可以看作一个损失，也可以看作一个L1正则化。C这个惩罚因子，C越大，越在意松弛因子的大小，容错空间越小；C越小，越不在意松弛因子，容错空间越大。如果C取正无穷，等价为Hard Margin SVM。
原问题如下：
${min?ω,b12ωTω+C∑imξis.t.yi(ωTxi+b)?1?ξi,i=1,2,...,mξi≥0,i=1,2,...,m\left \{ \begin{matrix} \min_{\omega,b} \quad \frac{1}{2} \omega^T\omega+C\sum_{i}^{m} \xi_i \\ s.t. \quad y_i(\omega^T x_i + b) \geqslant1-\xi_i ,\quad i=1,2,...,m \\ \xi_i \geq0,i=1,2,...,m \end{matrix} \right.$
对偶问题求解 $α\alpha$ 。变成如下形式：
${max?α∑i=1mαi?∑i=1m∑j=1mαiαjyiyjK(xi,xj)s.t.∑i=1mαiyi=00?αi?C,i=1,2,...,m\left \{ \begin{matrix} \max_{\alpha} \quad \sum_{i=1}^{m}\alpha_i - \sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_jK(x_i,x_j) \\ s.t. \sum_{i=1}^{m}\alpha_iy_i=0 \\ 0\leqslant \alpha_i \leqslant C,\quad i=1,2,...,m \end{matrix} \right.$
KKT条件是：
在这里插入图片描述

与支持向量机有关的回归算法

LSSVM

SVR

$\ \ \frac{1}{2}||w||^2+C\sum_{i=1}^{l}(\xi_i+\xi^*_i)\\ s.t. \ \ \left\{ \begin{aligned} &y_i-(w^Tx_i+b)<\epsilon+\xi_i \\ &(w^Tx_i+b)-y_i<\epsilon+\xi^*_i \\ &\xi_i,\xi^*_i\geq 0 \\ \end{aligned} \right.$
这部分主要讲svr的理解以及目标函数的推出。具体的求解参看西瓜书。
https://blog.csdn.net/Mbx8X9u/article/details/78153868

RVM

SVM的code

参考资料

前置知识：https://blog.csdn.net/L_15156024189/article/details/85182766，https://blog.csdn.net/the_lastest/article/details/78461566，https://en.wikipedia.org/wiki/Slater%27s_condition,https://en.wikipedia.org/wiki/Karush%E2%80%93Kuhn%E2%80%93Tucker_conditions，https://zhuanlan.zhihu.com/p/36621652
SVM:https://blog.csdn.net/macyang/article/details/38782399,https://www.cnblogs.com/wangyanphp/p/5498858.html,https://blog.csdn.net/m0_37687753/article/details/80964487,
https://blog.csdn.net/u014433413/article/details/78427574，https://blog.csdn.net/v_july_v/article/details/7624837，https://blog.csdn.net/weixin_44264662/article/details/97952385
SMO:https://blog.csdn.net/ACM_hades/article/details/90701030,https://www.cnblogs.com/pinard/p/6111471.html,https://www.bilibili.com/video/av70839977?p=31,https://zh.wikipedia.org/wiki/%E5%BA%8F%E5%88%97%E6%9C%80%E5%B0%8F%E4%BC%98%E5%8C%96%E7%AE%97%E6%B3%95,
http://cs229.stanford.edu/notes2019fall/cs229-notes3.pdf
SVR:https://blog.csdn.net/promisejia/article/details/81477439?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task,https://blog.csdn.net/qq_25037903/article/details/84789736?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task

支持向量机：PRML:SparseKernelMachine