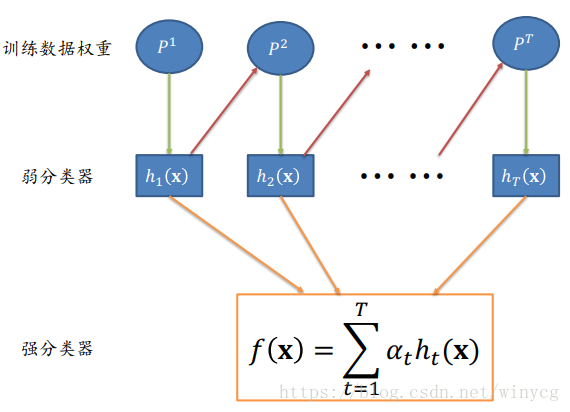
监督学习--Boosting (adaptive boosting, 自适应提升)：
对于一个复杂的分类任务，可以将其分解为 若干子任务，然后将若干子任务完成方法综合，最终完成该复杂任务。我们将这若干子任务称为弱分类器(weak classifiers)，然后将他们组合起来， 形成一个强分类器(strong classifier)。
在介绍自适应提升算法之前，我们先介绍一下计算学习理论 ( Computational Learning Theory)。
可计算：什么任务是可以计算的？能够被图灵可停机计算的任务。
可学习：什么任务是可以被学习的、从而被学习模型来完成。
计算学习理论：霍夫丁不等式(Hoeffding’s inequality)
- 学习任务：统计某个电视节目在全国的收视率。
- 方法：不可能去统计整个国家中每个人是否观看电视节目、进而算出收视率。 只能抽样一部分人口，然后将抽样人口中观看该电视节目的比例作为该电视 节目的全国收视率。
- 霍夫丁不等式：全国人口中看该电视节目的人口比例（记作?）与抽样人口中观看该电视节目的人口比例（记作?）满足如下关系：
当?足够大时，“全国人口中电视节目收视率”与“样本人口中电视节目收 视率”差值超过误差范围?的概率非常小。
计算学习理论：概率近似正确 (probably approximately correct, PAC)
对于统计电视节目收视率这样的任务，可以通过不同的采样方法（即 不同模型）来计算收视率。 每个模型会产生不同的误差。
问题：如果得到完成该任务的若干“弱模型”，是否可以将这些弱模 型组合起来，形成一个“强模型”。使该“强模型” 产生误差很小呢？ 这就是概率近似正确（PAC）要回答的问题。
在概率近似正确背景下，有“强可学习模型”和“弱可学习模型”
Adaboost使用整个训练集来训练弱学习机，训练样本在每次迭代中都会被赋予一个新的权重，在上一个学习机错误的基础上进行学习进而构建一个更加强大的分类器。
Ada Boosting算法中两个核心问题：
１、在每个弱分类器学习过程中，如何改变训练数据的权重：
提高在上 一轮中分类错误样本的权重。
２、如何将一系列弱分类器组合成强分类器：
通过加权多数表决方法来 提高分类误差小的弱分类器的权重，让其在最终分类中起到更大作用。同时减少分类误差大的弱分类器的权重，让其在最终分类中仅起到较小作用。
算法描述:
1.数据样本权重初始化
(1) 给定包含?个标注数据的训练集合Γ，
(2) Ada Boosting算法将从这些标注数据出发，训练得到一系列弱分类器，并 将这些弱分类器线性组合得到一个强分类器。
---1. 初始化每个训练样本的权重 :
2.第?个弱分类器训练
---2.对? = 1,2, … , ?
a) 使用具有分布权重??的训练数据来学习得到第?个基分类器（弱分类器） 
b) 计算
在训练数据集上的分类误差(被错误分类的样本所具有权重的累加) :
c) 计算弱分类器
的权重 ：
d) 更新训练样本数据的分布权重：
，其中??是归一 化因子以使得??+1为概率分布， 
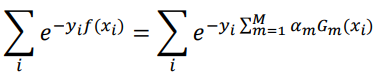
3.弱分类器组合成强分类器
---3. 以线性加权形式来组合弱分类器 f(x),分类能力越强的弱分类器具有更大权重:
(??累加之和并不等于1)
?(?)符号决定样本?分类为1或-1。如果 
为正，则强分类器?(?) 将样本?分类为1；否则为-1。
得到强分类器G(x):
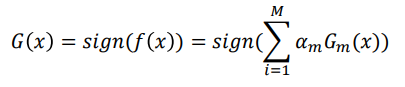
算法解释:
回看霍夫丁不等式:
--优化目标
Ada Boost实际在最小化如下指数损失函数(minimization of exponential loss )：
监督学习分为回归和分类两个类别。
- 在回归分析中，学习得到一个函数将输入变量映射到连续输出空间，如价格和温度等，即 值域是连续空间。
- 在分类模型中，学习得到一个函数将输入变量映射到离散输出空间，如人脸和汽车等，即 值域是离散空间。