关于数据结构Mooc后的每一道答案
基本我都已经给出了详解
希望能对大家有所帮助
收藏一下也是方便大家查找吧
希望大家一起进步!
(c语言)浙大数据结构Mooc作者答案集
原题题目(谷歌翻译)
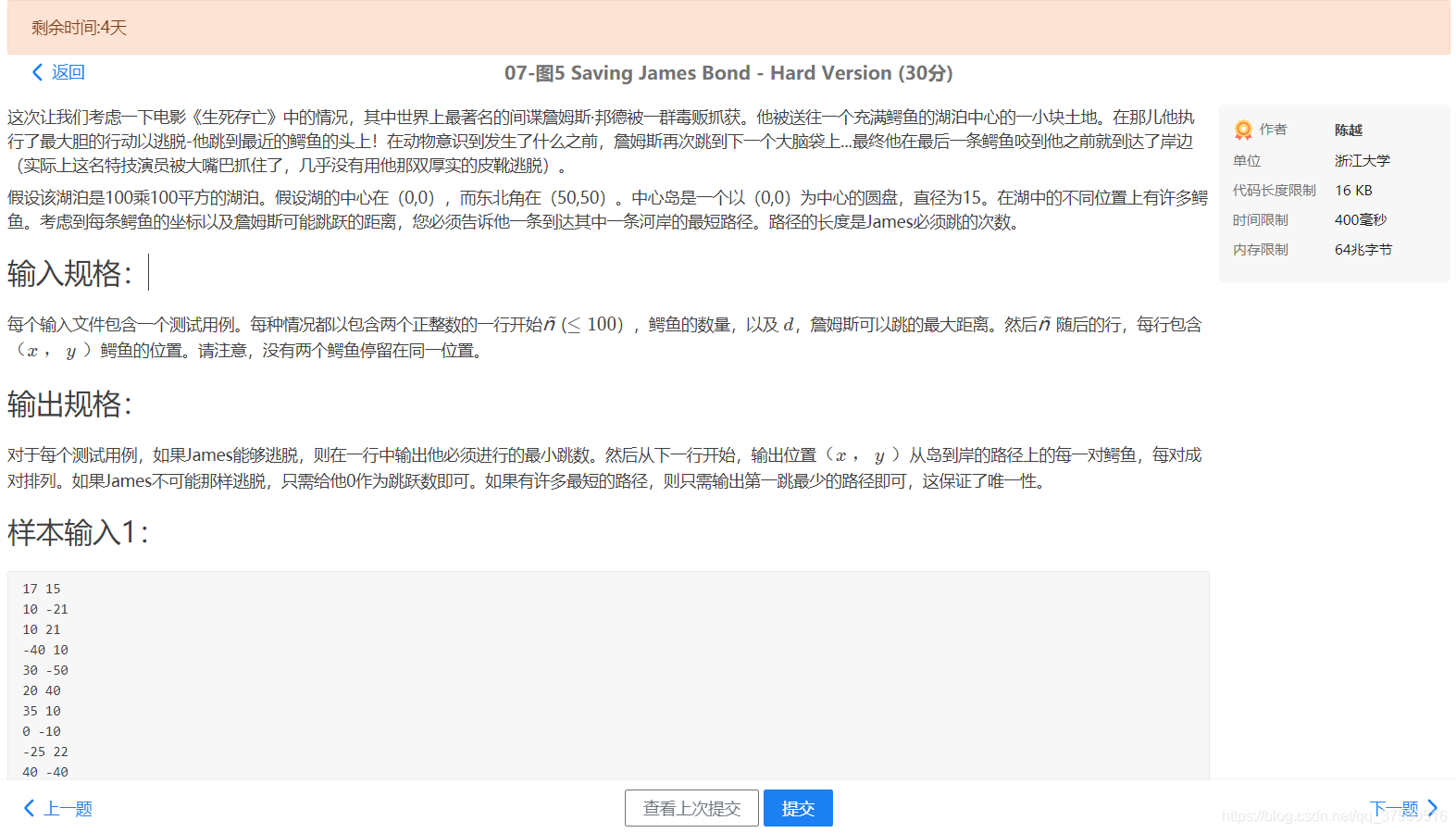
全检查点通过图
闲谈
说真的 第一次没有上CSDN
先瞄一眼人家的思路 然后再上手做这道题
自己完全独立做 竟然能够完全有思路
尤其在对于Dijkstra算法
这道题其实也就是变了一下形
就是把每条边的权值当成了1
然后再分别计算每个点的最短路径
只是还要考虑另外几个点
下面思路分析的时候 会专门讲的
总而言之 真的当这道题做出来的时候
我觉得喜悦的感觉已经少了很多了
更多的感觉是理所应当
这就是我应该做出来的题的感觉
现在也许比较刚开始处理一道题 根本不知所云
一道题可能思路都没有 看人家的解析都要看半天
甚至每道题都想放弃的感觉
可能现在真的 一点一点在进步了吧
再继续往下走吧
路还得一点一点慢慢走 饭也得一口口吃

解题思路
照例我们还是一部分一部分
慢慢来分析 把框架罗列出来
1、如何存储数值
这里需要我们存储一个图吗?
我认为是不需要的 我们只需要记录下来每个鳄鱼的点即可
因为我们只需要扫描
那些鳄鱼的点
然后判断距离我们是否能够跳到上面去即可
我们何必创造那些空的位置
我们还要花时间扫描那些空的点上面是否有数据呢
这里我使用的是一个结构体来记录点的位置
用结构体数组来记录所有鳄鱼的位置
结构体数组的0号位我们存储
007特工 ~bangbang(0,0)的位置
//设置110的原因是
//我们很多时候没有利用数组为0的地方
//而且很多我们提前定义的东西都要用到MAXN
//所以我干脆就扩大一点范围 从而避免段错误的问题
#define MAXN 110// 点类型的结构体
typedef struct
{
int x;int y;int stepnumber;//这里设置的firstjump是看我们第一步跳了多远//因为题目设置了说 当步数相同时 我们需要挑出来//跳第一步最近的即可 从而确定唯一路径//所以这个firstjump是我在最后才发现需要加的int firstjump;
} point;
point Point[MAXN];
2、如何判断能够到达岸边或者鳄鱼
很简单的
我们只需要一个Distance函数来判断
当我们跳跃的距离大于 两个点的距离即可
判断到达岸边这个
就是利用小学数学知识
你的当前位置的点 到岸边的距离绝对值小于等于你的跳跃距离
#include <math.h>//Distance函数
double Distance(point p1,point p2,int jumplength)
{
double distance = sqrt(pow(p1.x-p2.x,2) + pow(p1.y-p2.y,2));if(jumplength >= distance)return distance;elsereturn 0;
}//IsSafe函数
int IsSafe(point mypoint)
{
if(fabs(mypoint.x + 50) <= jumpability || fabs(mypoint.x - 50) <= jumpability || fabs(mypoint.y + 50) <= jumpability || fabs(mypoint.y - 50) <= jumpability)return 1;elsereturn 0;
}
3、如何确定最短路径(核心)
其实这里我刚开始想的是
我们做Easy Version的时候 用的
深度遍历 只要我们判断能否到达岸边即可
但是这道题与上次的题不同之处在于
我们还要处理 最短路径问题
还要再给出路径的具体坐标
所以我们这次就选择用 Dijkstra算法
不熟悉Dijkstra算法的可以回去看看
我关于这个算法写的博客
Dijkstra算法总结+例题+思路分析
但是肯定这道题也肯定不是照搬那个算法
算法的基础模板都是那样
我们需要在原题的基础上需要自己一定的理解+改动
下面直接给出代码
对于一些有点难理解的地方
我会给出注释
int ReDijkstra()
{
double islanddiameter = 15;int firstjump = INF;int i,j,number,min,temp,u,pointnumber,minstepnumber = INF;//首先这个地方 我们先把他和下面的过程单独分开//这个地方是我们第一次跳跃//其实也就类比为 我们Dijkstra的第一次取值//然后对我们的第一次能跳上去的鳄鱼赋初值for(i=1;i<=crocodiles;i++){
//注意这里 我对Point[i].firstjump赋于了初值//如果判断为距离小于我们跳跃距离 判断+赋值//方便最后的firstjump比较 从而确定逃跑唯一路径if(Point[i].firstjump = Distance(Point[0],Point[i],jumpability+islanddiameter/2)){
Point[i].stepnumber = Point[0].stepnumber + 1;Path[i]= 0;}}//下面基本就是我们Dijkstra算法模板for(i=1;i<=crocodiles;i++){
min = INF;temp = 0;for(j=1;j<=crocodiles;j++){
if(!Visit[j] && Point[j].stepnumber<min){
min = Point[j].stepnumber;temp = j;}}Visit[temp] = 1;for(u=0;u<=crocodiles;u++){
if(Distance(Point[temp],Point[u],jumpability)){
//注意 一般的Dijkstra是加上了权值//我们这道题的权值就是每条边是1 所以就加了1if(Point[u].stepnumber > Point[temp].stepnumber + 1){
Point[u].stepnumber = Point[temp].stepnumber + 1;Path[u] = temp;//如果temp的前面或temp第一跳越距离是什么//他后面只要是从它为起点的跳跃初值都是它temp的//可以简单理解为 一条路径从头到尾的第一跳距离都是一样的Point[u].firstjump = Point[temp].firstjump;//这里是对每个接触到的点进行判断是否能离岸并且记录//记录下来它在Point数组中位于第几个//下面还有对当路径值相等 firstjump进行比较的地方if(IsSafe(Point[u]) && Point[u].stepnumber + 1 <= minstepnumber){
if(Point[u].firstjump <= firstjump){
minstepnumber = Point[u].stepnumber + 1;pointnumber = u;firstjump = Point[u].firstjump;}}}}}}//因为我们对minstepnumber进行了初始化//如果minstepnumber值进行了改变 就说明有路径成功离岸了//如果没有改变 就说明 没有路径可以离开if(minstepnumber != INF)return pointnumber;elsereturn 0;
}
4、输出路径
我们需要用个堆栈从而把位置倒序进入堆栈
然后再从堆栈中取出即可
void Print(int pointnumber)
{
int i = pointnumber,queue[MAXN],top= -1 ,rear = -1;printf("%d\n",Point[i].stepnumber+1);//存储我们目标点上曾今走过的点//倒序输入for(;i!=0;i = Path[i])queue[++top] = i;//因为是倒序输入 所以正序输出就正过来了do{
printf("%d %d\n",Point[queue[top]].x,Point[queue[top]].y);top--;} while(top!=rear);return;
}
代码实现
#include <stdio.h>
#include <math.h>
#define MAXN 110
#define INF 999999//设置为全局变量 方便函数使用
int crocodiles,jumpability;//结构体
typedef struct
{
int x;int y;int stepnumber;int firstjump;
} point;//Point数组 Path路径数组 Visit访问数组
point Point[MAXN];
int Path[MAXN];
int Visit[MAXN];//插入鳄鱼节点 并对"我"的坐标相关数组点位初始化
void InsertCrocodiles()
{
int i,x,y;Point[0].x = 0;Point[0].y = 0;Point[0].stepnumber = 0;Point[0].firstjump = 0;Path[0] = -1;Visit[0] = 1;for(i=1;i<=crocodiles;i++){
scanf("%d %d",&x,&y);Point[i].x = x;Point[i].y = y;Point[i].stepnumber = INF;Visit[i] = 0;}return;
}//测量距离函数
double Distance(point p1,point p2,int jumplength)
{
double distance = sqrt(pow(p1.x-p2.x,2) + pow(p1.y-p2.y,2));if(jumplength >= distance)return distance;elsereturn 0;
}//判断能否离岸函数
int IsSafe(point mypoint)
{
if(fabs(mypoint.x + 50) <= jumpability || fabs(mypoint.x - 50) <= jumpability || fabs(mypoint.y + 50) <= jumpability || fabs(mypoint.y - 50) <= jumpability)return 1;elsereturn 0;
}//稍加改造的测量单源最短路径函数
int ReDijkstra()
{
double islanddiameter = 15;int firstjump = INF;int i,j,number,min,temp,u,pointnumber,minstepnumber = INF;for(i=1;i<=crocodiles;i++){
if(Point[i].firstjump = Distance(Point[0],Point[i],jumpability+islanddiameter/2)){
Point[i].stepnumber = Point[0].stepnumber + 1;Path[i]= 0;}}for(i=1;i<=crocodiles;i++){
min = INF;temp = 0;for(j=1;j<=crocodiles;j++){
if(!Visit[j] && Point[j].stepnumber<min){
min = Point[j].stepnumber;temp = j;}}Visit[temp] = 1;for(u=0;u<=crocodiles;u++){
if(Distance(Point[temp],Point[u],jumpability)){
if(Point[u].stepnumber > Point[temp].stepnumber + 1){
Point[u].stepnumber = Point[temp].stepnumber + 1;Path[u] = temp;Point[u].firstjump = Point[temp].firstjump;if(IsSafe(Point[u]) && Point[u].stepnumber + 1 <= minstepnumber){
if(Point[u].firstjump <= firstjump){
minstepnumber = Point[u].stepnumber + 1;pointnumber = u;firstjump = Point[u].firstjump;}}}}}}if(minstepnumber != INF)return pointnumber;elsereturn 0;
}//输出函数
void Print(int pointnumber)
{
int i = pointnumber,queue[MAXN],top= -1 ,rear = -1;printf("%d\n",Point[i].stepnumber+1);for(;i!=0;i = Path[i])queue[++top] = i;do{
printf("%d %d\n",Point[queue[top]].x,Point[queue[top]].y);top--;} while(top!=rear);return;
}//主函数
int main()
{
int answer = 0,pointnumber;double islanddiameter = 15;scanf("%d %d",&crocodiles,&jumpability);InsertCrocodiles();//这里是判断能否一步离岸 直接从岸边跳上去if(50 <= jumpability + islanddiameter/2)printf("1");else{
pointnumber = ReDijkstra();if(!pointnumber)printf("0");elsePrint(pointnumber);}return 0;
}
结束语
希望我的分析能对大家的思路有所启发
并对大家的解题有所帮助
大家一起共勉
