那我胖虎无话可说，只好从i为中心开始枚举，如果大于i,则让p[i]（回文长度）扩充到对称位置，然后再开始往后推演。
_(:з」∠)_量化分析的话可以搜索到的教程大概都会比我说的严谨与清楚许多，所以就说一下Manacher Algorithm的最主要的思想吧。。
为了方便地处理奇、偶回文串判别条件的区别，我们先将原串中所有字符之间增添一个原串中不曾出现的字符（我们假定为“#”）。
譬如说，abaaba，在增添后就变成了 #a#b#a#a#b#a，
这样，以#为中心的回文串，在原串中就是偶回文串。
然后，我们再规定两个数组与几个变量的意义:
数组Ma[i]：代表添加了“#”后的字符串。
数组Mp[i]：代表以字符串第i位为中心的回文串的最大长度。
变量Mx ：代表当前“已经匹配完毕的结尾最远的回文串”到达了Ma[]数组的第Mx位。
变量ID ：代表当前“已经匹配完毕的结尾最远的回文串”中心为Ma[]数组的第ID为。
不难发现，p[i]-1即是该回文串的长度……
在此……借用一下
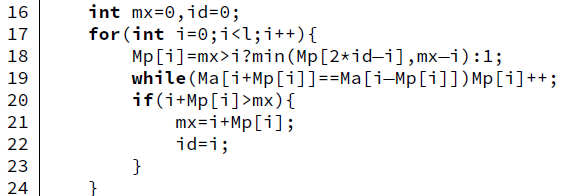我们来逐行看。
16行就不必说啦！
第17行，循环变量i代表了当前正在判断Ma串的第i位为中心的回文子串最长长度。
第十八行，是整个算法最核心的部分，也是O(n)时间复杂度的保障。
我们考虑到，假如当前的i已经被包含在曾经被判断过的回文串内（即Mx>i)，那么它在这个回文串中相对应的那个字符Ma[2*ID-i]，应当已经被计算过以它为中心的回文串可以有多长了。
那么，我们以第i位为中心的回文串长度，就有了第一个下限Mp[2*ID-i]。
但是，我们考虑到，以Ma[2*ID-i]为中心的回文串，它可能延展到了以Ma[ID]为中心的回文串之外。。这样我们就不能保证以Ma[i]为中心的回文串包括了以Ma[ID]为中心的回文串之外的部分。
所以我门得到了第二个下限Mx-i
综上，在Mx>i时，我们就得到了Mp[i]=min(Mp[2*id-i],mx-i);
第19行，考虑到第18行我们只得到了一个可怜的下限（……
我们要在这个下限的基础上继续向外扩展。
（画外音：教练，这个暴力匹配怎么保证复杂度还是O(n)呢！Σ( ° △ °|||)︴）
对于这一步的算法复杂度分析，我们可以分为三种情况！
考虑当前这一位i，在第18行的位置所执行的操作
①Mp[i]=1，说明Mx没有覆盖超过i，那么Mx的値在这一步执行后一定会增加。
②Mp[i]=Mx-i，说明以Ma[i]为中心的回文串至少到达了Mx，那么Mx的値在这之后不会减少。
③Mp[i]=Mp[ID*2-i]，说明可怜的Ma[i]只有这么长已经匹配不出去了。。T_T
考虑到，Mx的値是单调的，并且始终不会超过字符串长度Len，那么对于所有的i，①、②种情况的执行时间总和不会超过Len。因此总时间复杂度依旧是O(n)。