The Alias sample Method（复杂度为O(1)的采样算法）

原理请见:[https://www.keithschwarz.com/darts-dice-coins/]

代码运作距举例:

1.初始化

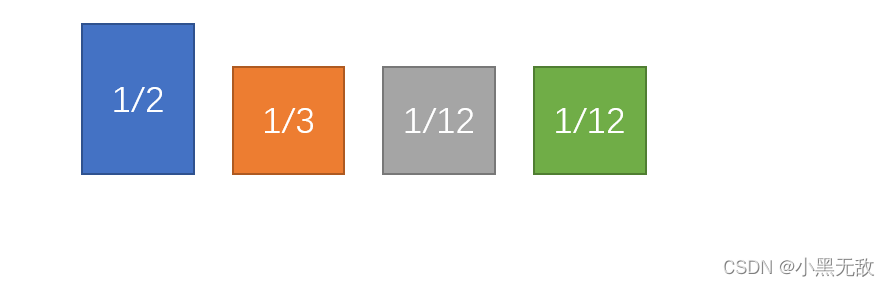
2.标准化(对应probs*len(probs))

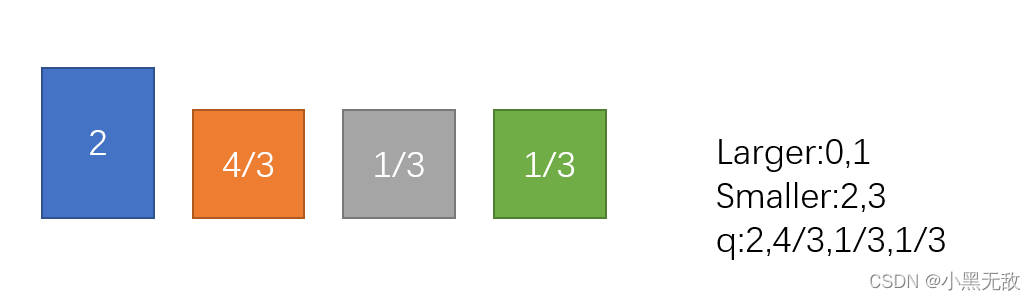
3.将结点1切分操作到结点3(结点1，3进行pop,进行概率切分)，之后结点1放入smaller

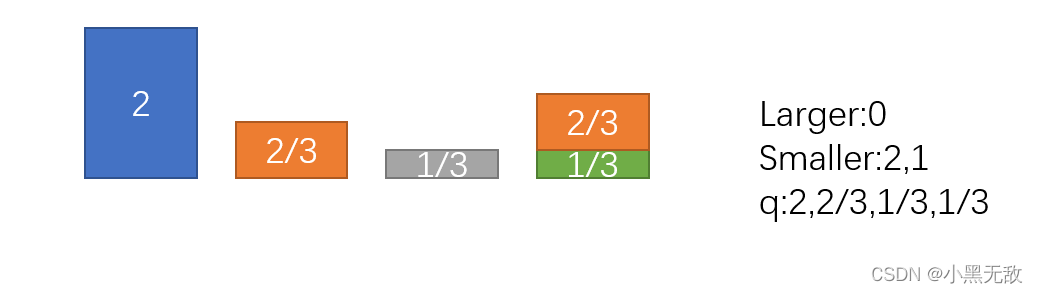
4.将结点0切分操作到结点2(结点0，2进行pop,进行概率切分)，之后结点0放入larger

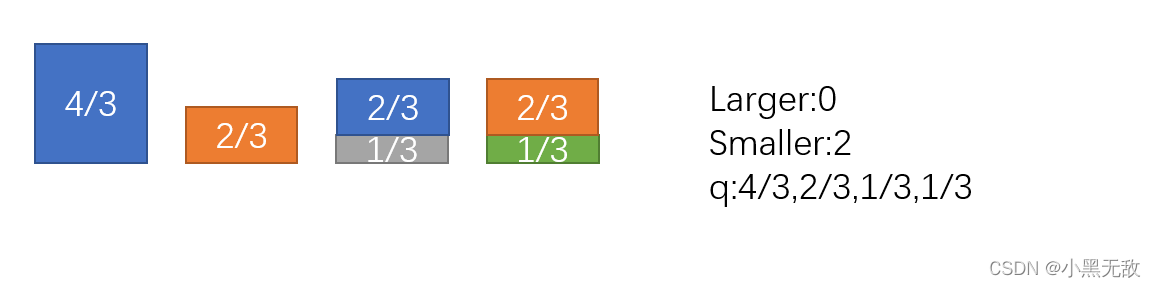
5.将结点0切分操作到结点1(结点0，1进行pop,进行概率切分)，最终完成切分任务。

代码实现:

def alias_setup(probs):# 初始化切分标记数组J和初始概率值qJ = np.zeros(len(probs))q = np.zeros(len(probs))smaller = []larger = []assert sum(probs) == 1.0# 标准化,probs = len(probs) * probs# 将事件分为两组,probs[i]大于1的为一组，小于一的为另一组for t,kk in enumerate(probs):q[t] = probs[t]*len(probs)if q[t] > 1.0:larger.append(t)else:smaller.append(t)while larger and smaller:large = larger.pop()small = smaller.pop()# 切大块，将小块补为1J[small] = large   q[large] = q[large] - (1 - q[small])if q[large] < 1.0:# 大块儿(大于1)变小块儿(小于1)smaller.append(large)else:# 大块儿依然是大块儿larger.append(large)return J,q
alias_setup([1/2,1/3,1/12,1/12])        

输出:
(array([0., 0., 0., 1.]),
array([1. , 0.66666667, 0.33333333, 0.33333333]))