''编号按照对应的内容,1-1代表第一大部分遇到的第一题,R代表Review,C代表运行的代码(Code)。
1-1.
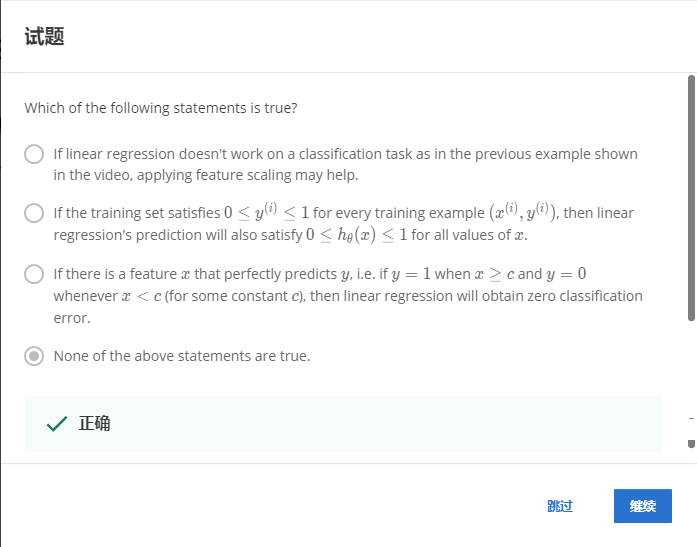
解:D
A:如果线性回归不适用于分类任务,就像前面的视频中的示例一样,应用特征缩放不会有所帮助,错误。
B:如果训练集满足0<yi<1,则对于a的所有值(xi,yi),线性回归的预测不满足0<h(x)<1,错误。线性回归的值是可以取一条直线,可以想象,除垂直于x轴外,其余直线的取值包含整个实数域。
C:如果特征x能完美预测y,x>=c时y=1,x<c时y=0线性分类将是零分类误差,错误。此问题尚未说明是二分类问题,y的取值不一定只有0和1。
1-2.
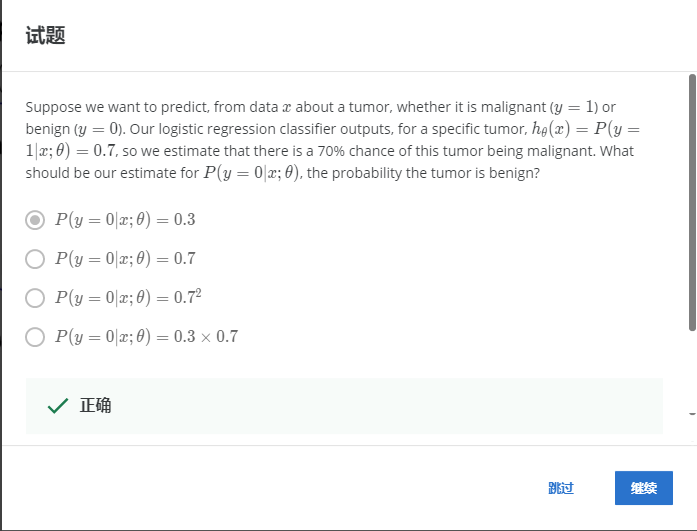
解:A
二分类问题中,y=0的概率与y=1的概率和为1。
1-3.
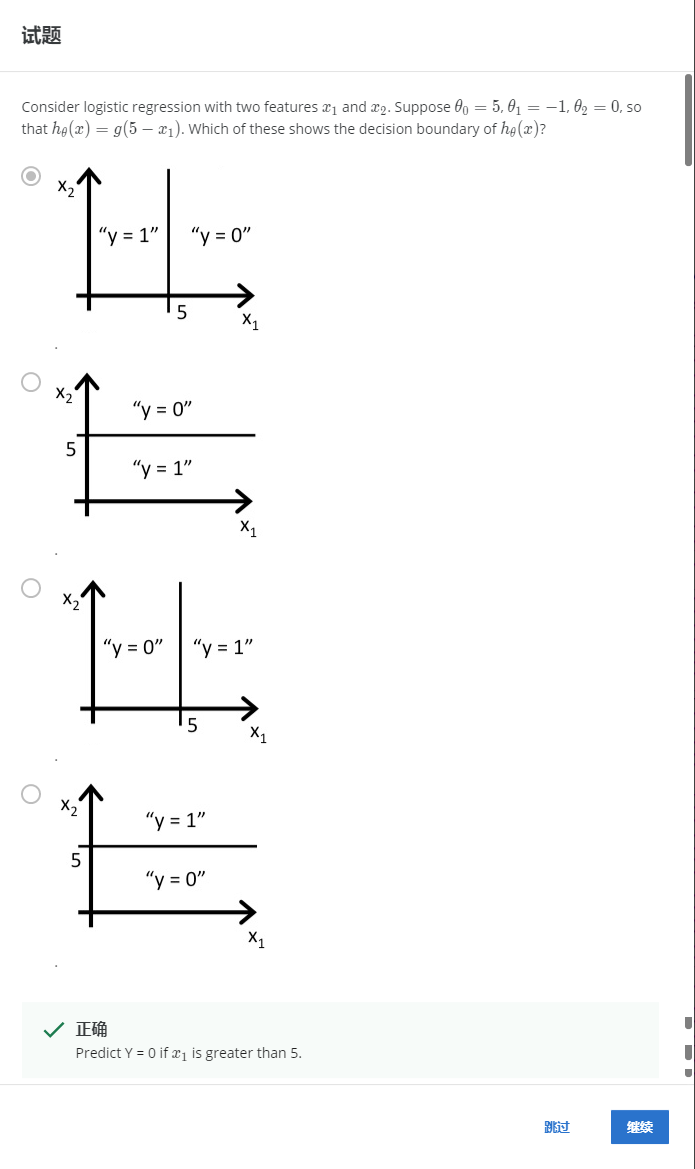
解:A
5-x1>0时y=1,即x1<5时y=1。
2-1.
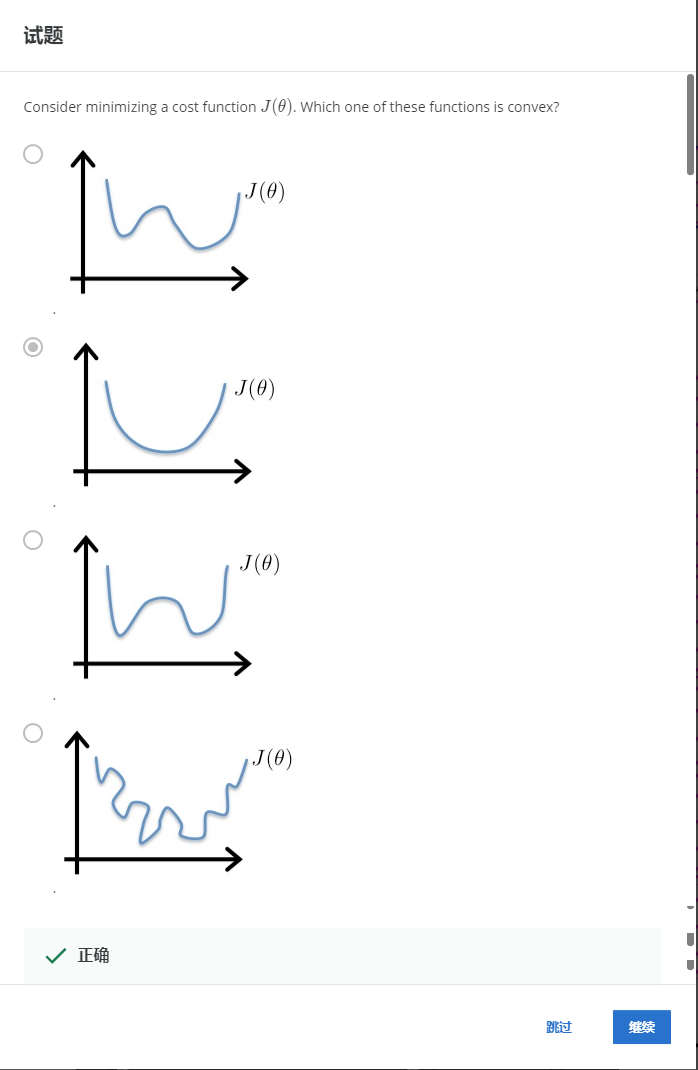
解:B
凸函数只有一个局部最优解,也是全局最优解。
2-2.
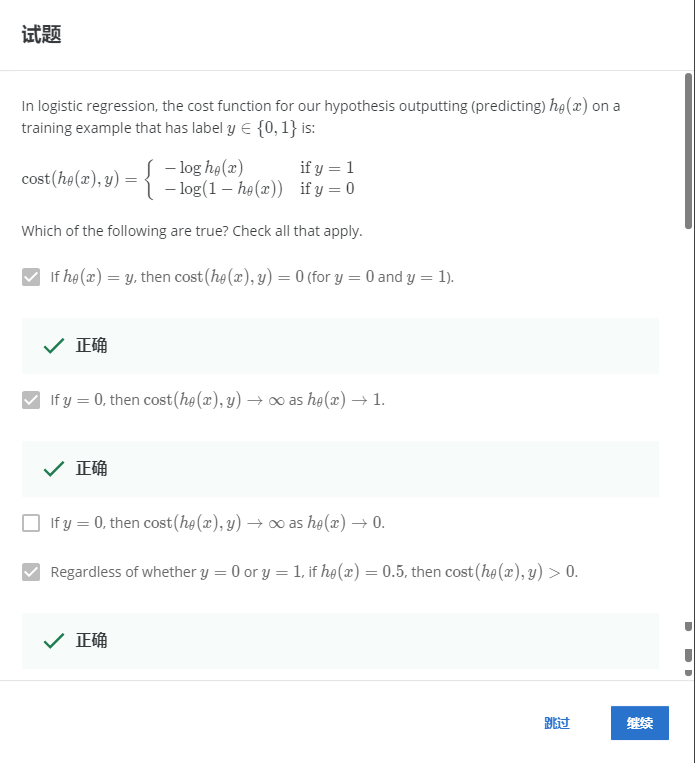
解:ABD
A:如果h函数能与y完美契合,那么代价函数值为0,正确。
B:如果y=0,h趋于1时代价函数趋于无穷,正确。
C:错误。
D:无论y=0还是y=1,如果h函数等于0.5,则与这两个值都有差距,故代价函数大于0,正确。
2-3.
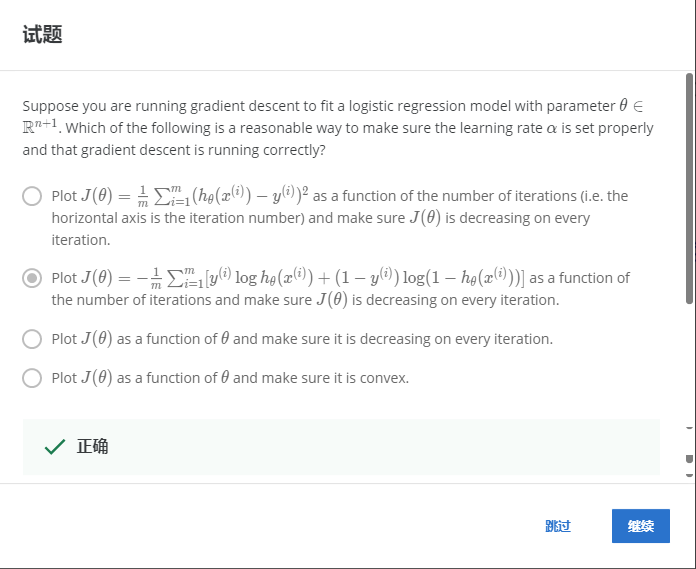
解:B
使用logistic的代价函数作为每次迭代的函数,这样就可以确保J(θ)在每次迭代中都减少。
2-4.
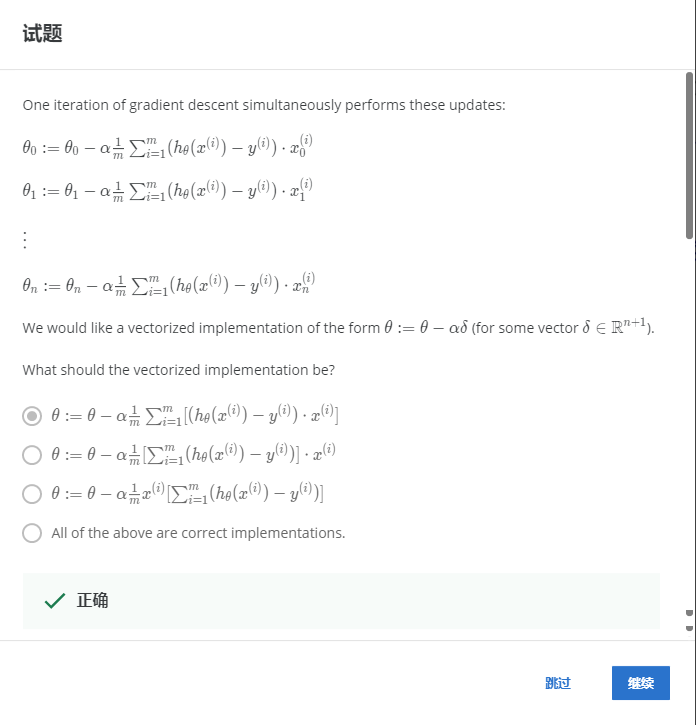
解:A
向量化的实现需要计算每个样本的误差和,只有A符合。
2-5.
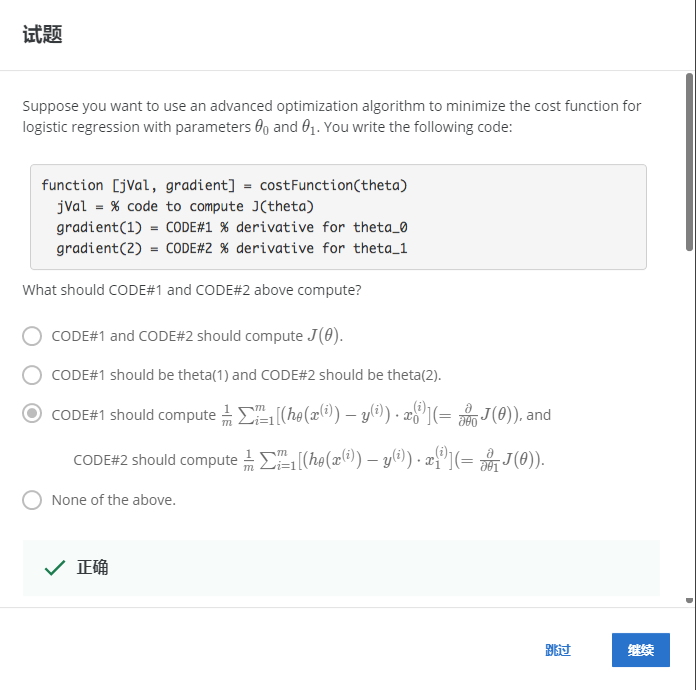
解:C
CODE1和CODE2属于不同的梯度更新,B应用的应该是theta(0)和theta(1)。
2-6.
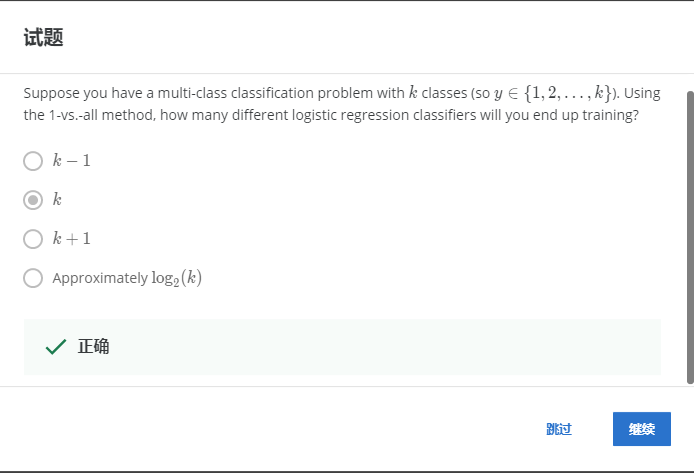
解:B
多分类,k类就需要k个分类器。
3-1.
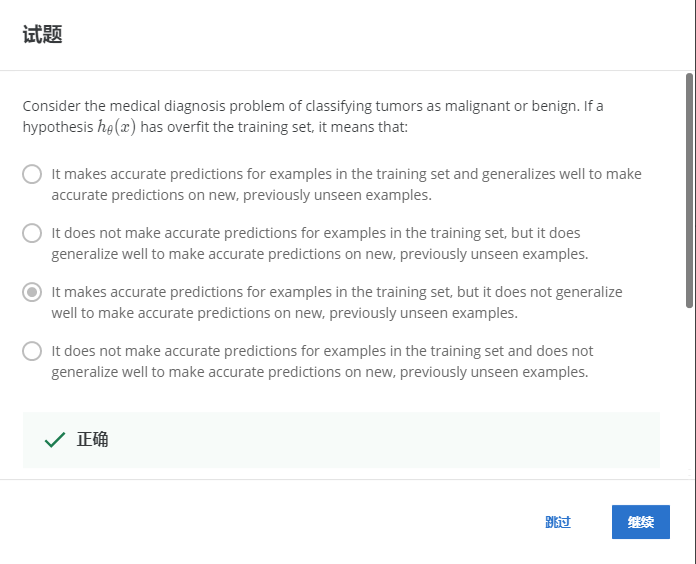
解:C
过拟合意味着在训练集上效果很好,在测试集上效果很差。
3-2.
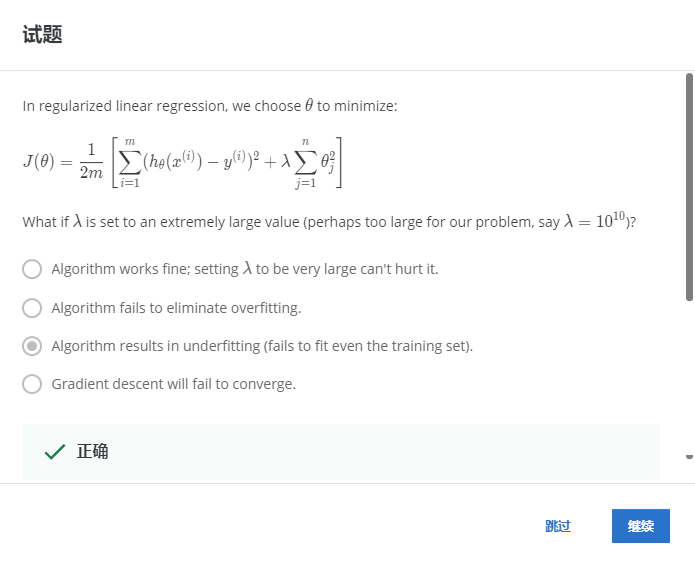
解:C
正则项λ设置的太大,图像上可以看出趋近于一条平行于x的一条直线,很容易就欠拟合。也可以这样理解,过大的λ也就代表了误差的对于函数J的影响变小,也就是代价函数主要受θ控制,而不再受误差影响。
3-3.

解:C
正则化后每次θ的系数会变小一点。
3-4.
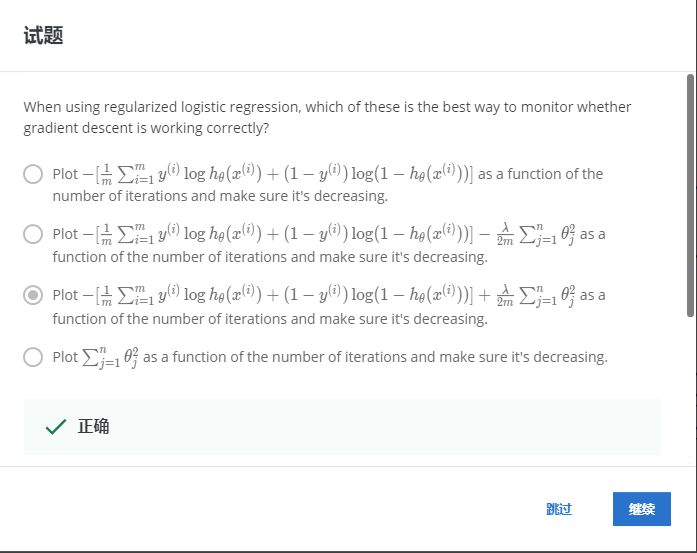
解:C
引入正则化是相加。
R
R1-1

解:AB
逻辑回归的值代表着类别为1的概率。
R1-2.

解:AB
A:添加多项式特征会提高训练数据的拟合程度,正确。
B:θ的最佳值时,我们的函数J大于等于0,正确。因为从图像中可以看出,使用这个模型不能完全拟合,存在着一定的误差。
C:添加多项式系数,拟合程度会变高,代价函数J会下降,错误。
D:逻辑回归函数h的值不可能大于1,错误。
R1-3.

解:AB
A中的h函数可以用B中对应位置的函数代替。
R1-4.

解:AB
A:因为H_theta(x)总是0到1,故CostFunction按照定义一定是大于等于0的,正确。
B:sigmoid函数对的值不会大于1,正确。罗辑回归可以使用“区分一类和其他剩下类”的方法
C:如果使用线性回归所做预测的阈值进行分类,线性回归对分类并非总有很好的效果,错误。
D:逻辑回归是凸函数的优化,逻辑回归一定会收敛到全局最优解,错误。
R1-5.
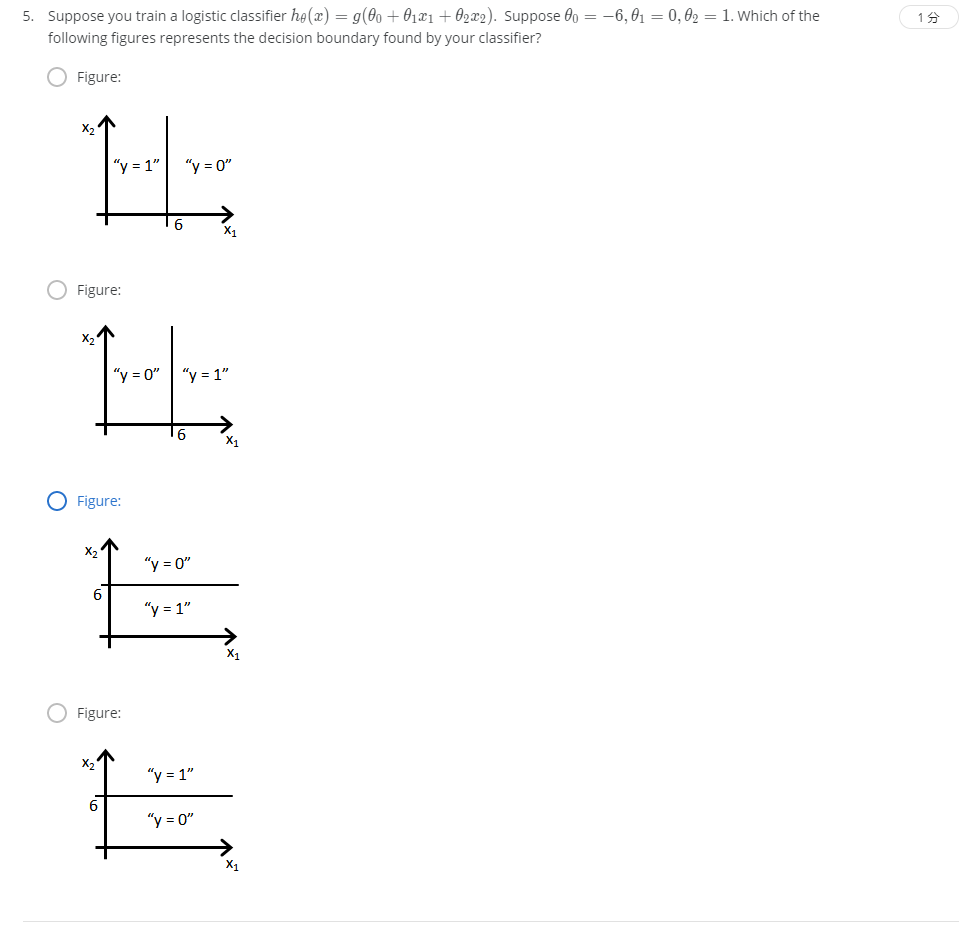
解:D
-6+x2>0时y=1,即x2>6时y=1。
R2-1.

解:D
A:添加新的特征不能避免过拟合,错误。
B:引入正则化并非会在训练集上表现得更好,一般来说会变差,错误。
C:引入正则化也不一定会在非训练数据集中表现更好,错误。
D:添加一个新特征一定会在训练数据集中表现的更好,正确。
R2-2.

解:A
引入正则化后θ会变得更小。
R2-3.

解:B
A:使用过大的λ会导致欠拟合,错误。
B:分类问题中,如果引入正则化,会导致部分的训练数据错误分类,正确。
C:使用过大的λ值会导致更差的h函数的表现,错误。
D:正则化对逻辑回归也有效果,错误。
R2-4.
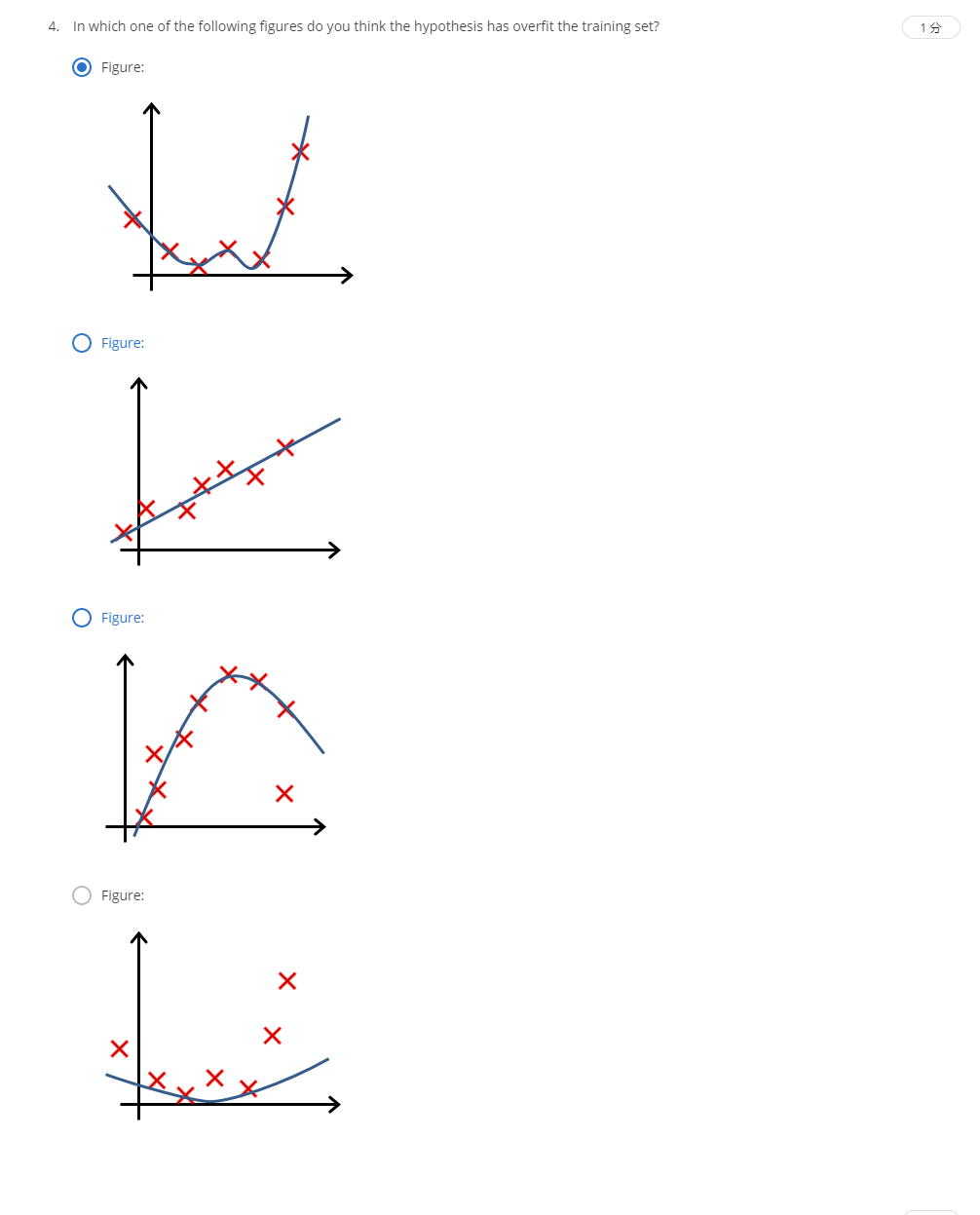
解:A
低误差,高准确度,预测曲线又太过复杂。
R2-5.
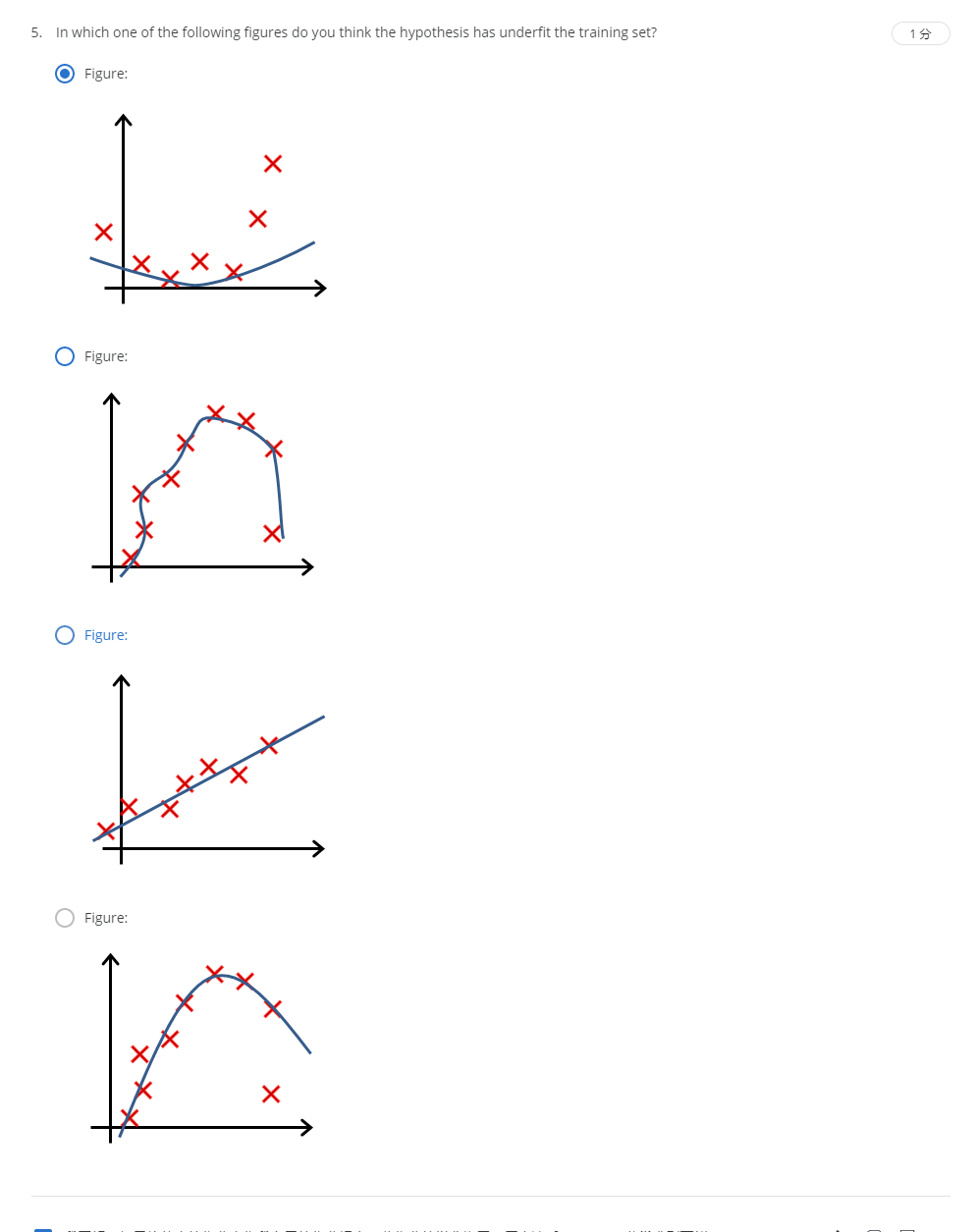
解:A
有很多数据点都不在曲线上。