原文链接:https://blog.csdn.net/u013733326/article/details/79866913
第3周测验 - 浅层神经网络
1.以下哪一项是正确的?([] ()是上标,后面紧跟着)
- X是一个矩阵,其中每个列都是一个训练示例。
- a[2]4是第二层第四层神经元的激活的输出。
a[2](12)a[2](12)表示第二层和第十二层的激活向量。- a[2]a[2] 表示第二层的激活向量。
解:1 2 3 4
X的每一列都是一个样本,然后是样本向量的横向堆叠。
[]代表层数。
2.tanh激活函数通常比隐藏层单元的sigmoid激活函数效果更好,因为其输出的平均值更接近于零,因此它将数据集中在下一层是更好的选择,请问正确吗?
- True
- False
解:1
请注意,你可以看一下https://stats.stackexchange.com/a/101563/169377 和http://yann.lecun.com/exdb/publis/pdf/lecun-98b.pdf
As seen in lecture the output of the tanh is between -1 and 1, it thus centers the data which makes the learning simpler for the next layer.
正如视频中所看到的,tanh的输出在-1和1之间,因此它将数据集中在一起,使得下一层的学习变得更加简单。
3.其中哪一个是第l层向前传播的正确向量化实现,其中1≤l≤L
Z[l]=W[l]A[l?1]+b[l]A[l]=g[l](Z[l])
4.您正在构建一个识别黄瓜(y = 1)与西瓜(y = 0)的二元分类器。 你会推荐哪一种激活函数用于输出层?
- ReLU
- Leaky ReLU
- sigmoid
- tanh
解:3
来自sigmoid函数的输出值可以很容易地理解为概率。
Sigmoid outputs a value between 0 and 1 which makes it a very good choice for binary classification. You can classify as 0 if the output is less than 0.5 and classify as 1 if the output is more than 0.5. It can be done with tanh as well but it is less convenient as the output is between -1 and 1.
Sigmoid输出的值介于0和1之间,这使其成为二元分类的一个非常好的选择。 如果输出小于0.5,则可以将其归类为0,如果输出大于0.5,则归类为1。 它也可以用tanh来完成,但是它不太方便,因为输出在-1和1之间。
5.看一下下面的代码:
A = np.random.randn(4,3)
B = np.sum(A, axis = 1, keepdims = True)
请问B.shape的值是多少?
B.shape = (4, 1),axis是指整合到第1维度,所以就变成了(4, 1)。
we use (keepdims = True) to make sure that A.shape is (4,1) and not (4, ). It makes our code more rigorous.
我们使用(keepdims = True)来确保A.shape是(4,1)而不是(4,),它使我们的代码更加严格。
6.假设你已经建立了一个神经网络。 您决定将权重和偏差初始化为零。 以下哪项陈述是正确的?
- 第一个隐藏层中的每个神经元节点将执行相同的计算。 所以即使经过多次梯度下降迭代后,层中的每个神经元节点都会计算出与其他神经元节点相同的东西。
- 第一个隐藏层中的每个神经元将在第一次迭代中执行相同的计算。 但经过一次梯度下降迭代后,他们将学会计算不同的东西,因为我们已经“破坏了对称性”。
- 第一个隐藏层中的每一个神经元都会计算出相同的东西,但是不同层的神经元会计算不同的东西,因此我们已经完成了“对称破坏”。
- 即使在第一次迭代中,第一个隐藏层的神经元也会执行不同的计算, 他们的参数将以自己的方式不断发展。
解:1
如果每层的神经元都进行相同的计算,如果同时初始化为0,那么他们就具有对称性,与一个神经元的效果相同。
7.Logistic回归的权重w应该随机初始化,而不是全零,因为如果初始化为全零,那么逻辑回归将无法学习到有用的决策边界,因为它将无法“破坏对称性”,是正确的吗?
- True
- False
解:2
Logistic Regression doesn’t have a hidden layer. If you initialize the weights to zeros, the first example x fed in the logistic regression will output zero but the derivatives of the Logistic Regression depend on the input x (because there’s no hidden layer) which is not zero. So at the second iteration, the weights values follow x’s distribution and are different from each other if x is not a constant vector.
Logistic回归没有隐藏层。 如果将权重初始化为零,则Logistic回归中的第一个示例x将输出零,但Logistic回归的导数取决于不是零的输入x(因为没有隐藏层)。 因此,在第二次迭代中,如果x不是常量向量,则权值遵循x的分布并且彼此不同。
8.您已经为所有隐藏单元使用tanh激活建立了一个网络。 使用np.random.randn(…,…) 1000将权重初始化为相对较大的值。 会发生什么?*
- 这没关系。只要随机初始化权重,梯度下降不受权重大小的影响。
- 这将导致tanh的输入也非常大,因此导致梯度也变大。因此,您必须将α设置得非常小以防止发散; 这会减慢学习速度。
- 这会导致tanh的输入也非常大,导致单位被“高度激活”,从而加快了学习速度,而权重必须从小数值开始。
- 这将导致tanh的输入也很大,因此导致梯度接近于零, 优化算法将因此变得缓慢。
解:4
tanh becomes flat for large values, this leads its gradient to be close to zero. This slows down the optimization algorithm.
tanh对于较大的值变得平坦,这导致其梯度接近于零。 这减慢了优化算法。
9.看一下下面的单隐层神经网络:
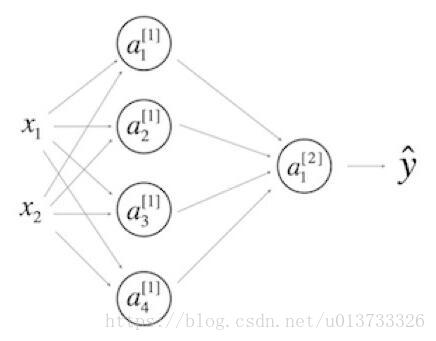
- b[1]的维度是(4, 1)
- W[1] 的维度是 (4, 2)
- W[2]的维度是 (1, 4)
- b[2]的维度是 (1, 1)
解:1 2 3 4
W[i]后面对应的是(i层的神经元数目,i-1层的神经元数目)
请注意: 点击https://user-images.githubusercontent.com/14886380/29200515-7fdd1548-7e88-11e7-9d05-0878fe96bcfa.png来看一下公式。
10.I在和上一个相同的网络中,z[1]和 A[1]的维度是多少?
- z[1]和A[1]的维度都是 (4,m)
解:1
同一层的z的维度和A的相同,m是样本数目。
请注意: 点击https://user-images.githubusercontent.com/14886380/29200515-7fdd1548-7e88-11e7-9d05-0878fe96bcfa.png来看一下公式。