吴恩达 deeplearning.ai - 改善深层神经网络 - 第2周代码

参考链接： https://blog.csdn.net/u013733326/article/details/79907419

开始之前

在正式开始之前，我们说一下我们要做什么。我们需要做的是分割数据集和优化梯度下降算法，所以我们需要做以下几件事：

1. 分割数据集

2. 优化梯度下降算法：

   2.1 不使用任何优化算法

   2.2 mini-batch梯度下降法

   2.3 使用具有动量的梯度下降算法

   2.4 使用Adam算法

导入库函数

# -*- coding: utf-8 -*-import numpy as np
import matplotlib.pyplot as plt
import scipy.io
import math
import sklearn
import sklearn.datasetsimport opt_utils #参见数据包或者在本文底部copy
import testCase  #参见数据包或者在本文底部copy#%matplotlib inline #如果你用的是Jupyter Notebook请取消注释
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

D:\workspace\Python\jupyter\DeepLearingAI\lecture1\lecture2\week2\opt_utils.py:76: SyntaxWarning: assertion is always true, perhaps remove parentheses?assert(parameters['W' + str(l)].shape == layer_dims[l], layer_dims[l-1])
D:\workspace\Python\jupyter\DeepLearingAI\lecture1\lecture2\week2\opt_utils.py:77: SyntaxWarning: assertion is always true, perhaps remove parentheses?assert(parameters['W' + str(l)].shape == layer_dims[l], 1)

梯度下降

在机器学习中，最简单就是没有任何优化的梯度下降(GD,Gradient Descent)，我们每一次循环都是对整个训练集进行学习，这叫做批量梯度下降(Batch Gradient Descent)

def update_parameters_with_gd(parameters, grads, learning_rate):'''使用梯度下降更新参数参数：parameters - 字典，包含了要更新的参数：parameters['W' + str(l)] = Wlparameters['b' + str(l)] = blgrads - 字典，包含了每一个梯度值用以更新参数grads['dW' + str(l)] = dWlgrads['db' + str(l)] = dbllearning_rate - 学习率返回值：parameters - 字典，包含了更新后的参数'''L = len(parameters)//2 #神经网络的层数# 更新每个参数for l in range(L):parameters['W'+str(l+1)] = parameters['W'+str(l+1)]-learning_rate*grads['dW'+str(l+1)]parameters['b'+str(l+1)] = parameters['b'+str(l+1)]-learning_rate*grads['db'+str(l+1)]return parameters

测试一下

#测试update_parameters_with_gd
print("-------------测试update_parameters_with_gd-------------")
parameters , grads , learning_rate = testCase.update_parameters_with_gd_test_case()
parameters = update_parameters_with_gd(parameters,grads,learning_rate)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))

-------------测试update_parameters_with_gd-------------
W1 = [[ 1.63535156 -0.62320365 -0.53718766][-1.07799357  0.85639907 -2.29470142]]
b1 = [[ 1.74604067][-0.75184921]]
W2 = [[ 0.32171798 -0.25467393  1.46902454][-2.05617317 -0.31554548 -0.3756023 ][ 1.1404819  -1.09976462 -0.1612551 ]]
b2 = [[-0.88020257][ 0.02561572][ 0.57539477]]

由梯度下降算法演变来的还有随机梯度下降（SGD）算法和小批量梯度下降算法，随机梯度下降（SGD），相当于小批量梯度下降，但是和mini-batch不同的是其中每个小批量(mini-batch)仅有1个样本，和梯度下降不同的是你一次只能在一个训练样本上计算梯度，而不是在整个训练集上计算梯度。我们来看一下它们的差异：

#仅做比较，不运行。# #批量梯度下降，又叫梯度下降
# X = data_input
# Y = labels# parameters = initialize_parameters(layers_dims)
# for i in range(0,num_iterations):
# #前向传播
# A,cache = forward_propagation(X,parameters)
# #计算损失
# cost = compute_cost(A,Y)
# #反向传播
# grads = backward_propagation(X,Y,cache)
# #更新参数
# parameters = update_parameters(parameters,grads)# #随机梯度下降算法：
# X = data_input
# Y = labels
# parameters = initialize_parameters(layers_dims)
# for i in (0, num_iterations):
# for j in m:
# #前向传播
# A,cache = forward_propagation(X,parameters)
# #计算成本
# cost = compute_cost(A,Y)
# #后向传播
# grads = backward_propagation(X,Y,cache)
# #更新参数
# parameters = update_parameters(parameters,grads)

在随机梯度下降算法中，每次迭代中仅使用其中一个样本，当训练集很大时，使用随机梯度下降算法的运行速度会很快，但是会存在一定的波动。

在随机梯度下降中，在更新梯度之前，只使用1个训练样本。 当训练集较大时，随机梯度下降可以更快，但是参数会向最小值摆动，而不是平稳地收敛，我们来看一下比较图:

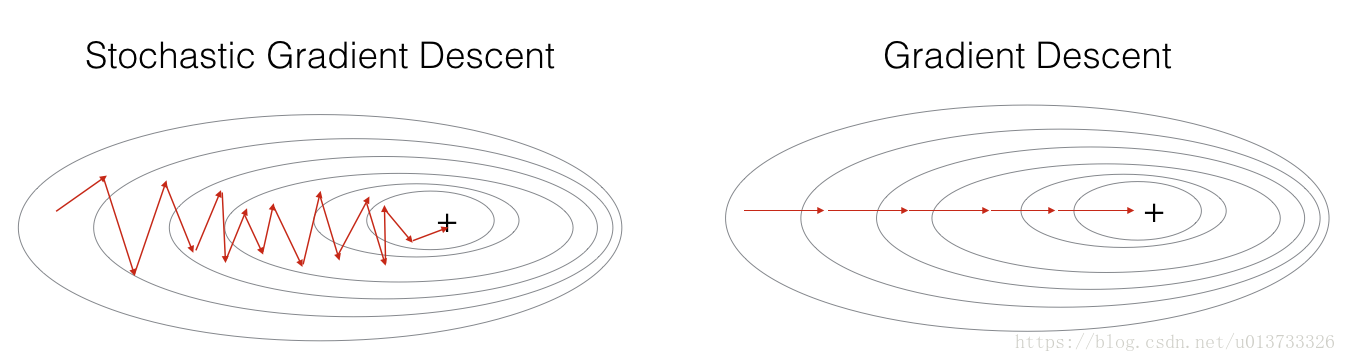
在实际中，更好的方法是使用小批量(mini-batch)梯度下降法，小批量梯度下降法是一种综合了梯度下降法和随机梯度下降法的方法，在它的每次迭代中，既不是选择全部的数据来学习，也不是选择一个样本来学习，而是把所有的数据集分割为一小块一小块的来学习，它会随机选择一小块（mini-batch），块大小一般为2的n次方倍。一方面，充分利用的GPU的并行性，更一方面，不会让计算时间特别长，来看一下比较图：

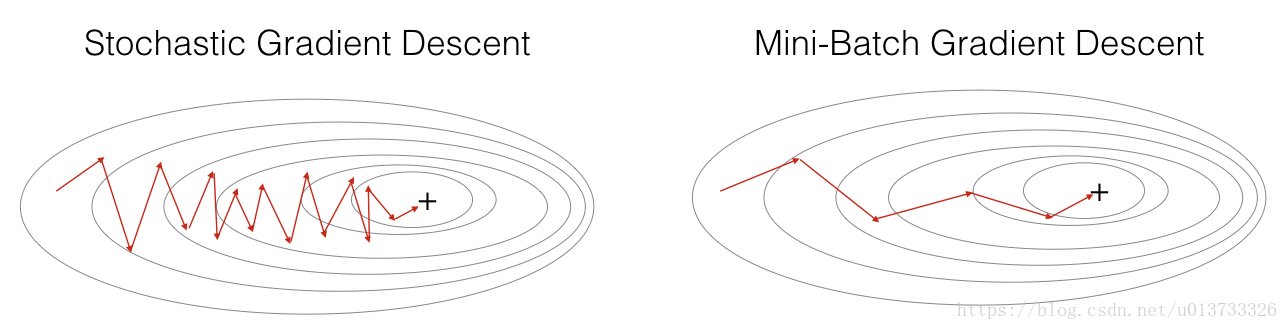
mini-batch梯度下降法

我们要使用mini-batch要经过两个步骤：

1. 把训练集打乱，但是X和Y依旧是一一对应的，之后，X的第i列是与Y中的第i个标签对应的样本。

2. 切分，我们把训练集打乱之后，我们就可以对它进行切分了。

def random_mini_batches(X, Y, mini_batch_size=64, seed=0):'''从（X，Y）中创建一个随机的mini-batch列表参数：X - 输入数据，维度为(输入节点数量，样本的数量)Y - 对应的是X的标签，【1 | 0】（蓝|红），维度为(1,样本的数量)mini_batch_size - 每个mini-batch的样本数量返回：mini-bacthes - 一个同步列表，维度为（mini_batch_X,mini_batch_Y）'''# 设置随机数种子np.random.seed(seed)# 样本数量m = X.shape[1]mini_batches = []# 1：打乱顺序# 充当索引permutation = list(np.random.permutation(m)) # 它返回一个长度为m的随机数组，且里面的数是0到m-1shuffled_X = X[:, permutation] #按照permutation的顺序来重新排序# 转化为行向量shuffled_Y = Y[:,permutation].reshape((1, m))# 2：分割# 把你的训练集分割成多少份,请注意，如果值是99.99，那么返回值是99，剩下的0.99会被舍弃num_complete_minibatches = math.floor(m / mini_batch_size)for k in range(0, num_complete_minibatches):# 分成不同的块mini_batch_X = shuffled_X[:, k*mini_batch_size:(k+1)*mini_batch_size]mini_batch_Y = shuffled_Y[:, k*mini_batch_size:(k+1)*mini_batch_size]# 整合结果mini_batch = (mini_batch_X, mini_batch_Y)# 记录结果mini_batches.append(mini_batch)# 如果训练集的大小刚好是mini_batch_size的整数倍，那么已经处理完了# 如果不是整数倍，那么肯定会剩下一些，我们对这些数据也需要进行处理if m%mini_batch_size != 0:# 获取最后剩余的部分mini_batch_X = shuffled_X[:, mini_batch_size*num_complete_minibatches:]mini_batch_Y = shuffled_Y[:, mini_batch_size*num_complete_minibatches:]mini_batch = (mini_batch_X,mini_batch_Y)mini_batches.append(mini_batch)return mini_batches

测试一下

#测试random_mini_batches
print("-------------测试random_mini_batches-------------")
X_assess,Y_assess,mini_batch_size = testCase.random_mini_batches_test_case()
mini_batches = random_mini_batches(X_assess,Y_assess,mini_batch_size)print("第1个mini_batch_X 的维度为：",mini_batches[0][0].shape)
print("第1个mini_batch_Y 的维度为：",mini_batches[0][1].shape)
print("第2个mini_batch_X 的维度为：",mini_batches[1][0].shape)
print("第2个mini_batch_Y 的维度为：",mini_batches[1][1].shape)
print("第3个mini_batch_X 的维度为：",mini_batches[2][0].shape)
print("第3个mini_batch_Y 的维度为：",mini_batches[2][1].shape)

-------------测试random_mini_batches-------------
第1个mini_batch_X 的维度为： (12288, 64)
第1个mini_batch_Y 的维度为： (1, 64)
第2个mini_batch_X 的维度为： (12288, 64)
第2个mini_batch_Y 的维度为： (1, 64)
第3个mini_batch_X 的维度为： (12288, 20)
第3个mini_batch_Y 的维度为： (1, 20)

包含动量的梯度下降（Momentum）

由于小批量梯度下降只看到了一个子集的参数更新，更新的方向有一定的差异，所以小批量梯度下降的路径将“振荡地”走向收敛，使用动量可以减少这些振荡，动量考虑了过去的梯度以平滑更新， 我们将把以前梯度的方向存储在变量v中，从形式上讲，这将是前面的梯度的指数加权平均值。我们也可以把V看作是滚下坡的速度，根据山坡的坡度建立动量。我们来看一下下面的图：

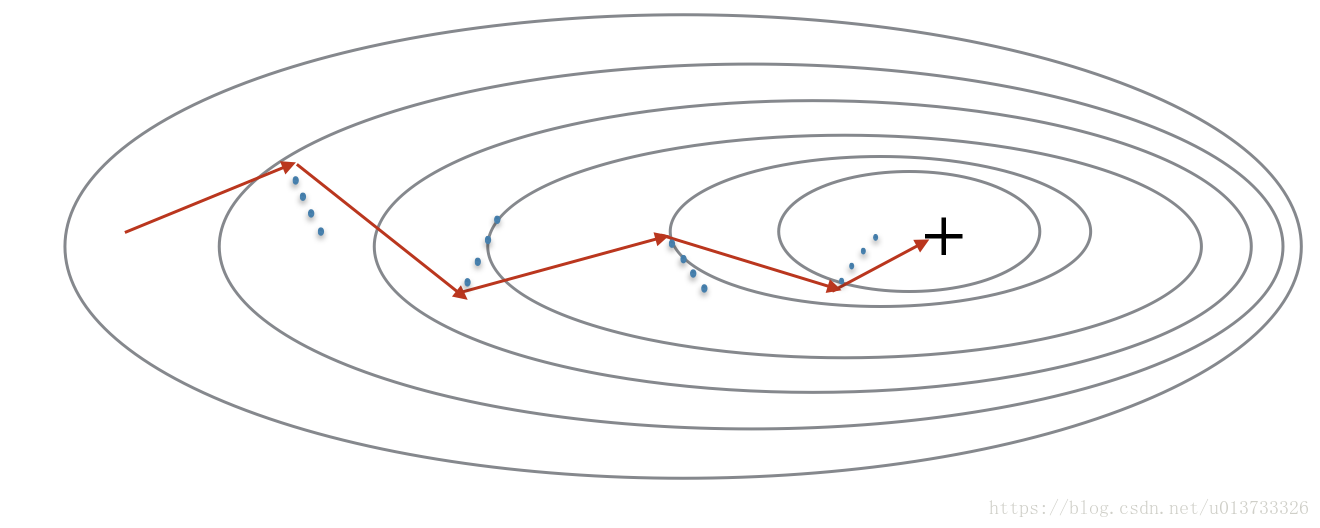
红色箭头显示具有动量的小批量梯度下降一步时所采取的方向，蓝色的点显示每个步骤的梯度方向（相对于当前的小批量）。然我们不仅要观察梯度，还要让$v$影响梯度，然后朝$v$方向前进一步,尽量让前进的方向指向最小值。既然我们要影响梯度的方向，而梯度需要使用到dW和db，那么我们就要建立一个和dW和db相同结构的变量来影响他们，开始初始化：

def initialize_velocity(parameters):'''初始化速度，velocity是一个字典：- keys: "dW1", "db1", ..., "dWL", "dbL" - values:与相应的梯度/参数维度相同的值为零的矩阵。参数：parameters - 一个字典，包含了以下参数：parameters["W" + str(l)] = Wlparameters["b" + str(l)] = bl返回:v - 一个字典变量，包含了以下参数：v["dW" + str(l)] = dWl的速度v["db" + str(l)] = dbl的速度'''L = len(parameters)//2 #神经网络层数v = {
    }for l in range(L):v['dW'+str(l+1)] = np.zeros_like(parameters['W'+str(l+1)])v['db'+str(l+1)] = np.zeros_like(parameters['b'+str(l+1)])return v

测试一下

#测试initialize_velocity
print("-------------测试initialize_velocity-------------")
parameters = testCase.initialize_velocity_test_case()
v = initialize_velocity(parameters)print('v["dW1"] = ' + str(v["dW1"]))
print('v["db1"] = ' + str(v["db1"]))
print('v["dW2"] = ' + str(v["dW2"]))
print('v["db2"] = ' + str(v["db2"]))

-------------测试initialize_velocity-------------
v["dW1"] = [[0. 0. 0.][0. 0. 0.]]
v["db1"] = [[0.][0.]]
v["dW2"] = [[0. 0. 0.][0. 0. 0.][0. 0. 0.]]
v["db2"] = [[0.][0.][0.]]

使用相关公式进行带有动量的参数更新

def update_parameters_with_momentun(parameters, grads, v, beta, learning_rate):'''使用动量更新参数参数：parameters - 一个字典类型的变量，包含了以下字段：parameters["W" + str(l)] = Wlparameters["b" + str(l)] = blgrads - 一个包含梯度值的字典变量，具有以下字段：grads["dW" + str(l)] = dWlgrads["db" + str(l)] = dblv - 包含当前速度的字典变量，具有以下字段：v["dW" + str(l)] = ...v["db" + str(l)] = ...beta - 超参数，动量，实数learning_rate - 学习率，实数返回：parameters - 更新后的参数字典v - 包含了更新后的速度变量'''L = len(parameters)//2 #神经网络层数for l in range(L):# 计算速度v['dW'+str(l+1)] = beta*v['dW'+str(l+1)]+(1-beta)*grads['dW'+str(l+1)]v['db'+str(l+1)] = beta*v['db'+str(l+1)]+(1-beta)*grads['db'+str(l+1)]# 更新参数parameters['W'+str(l+1)] = parameters['W'+str(l+1)]-learning_rate*v['dW'+str(l+1)]parameters['b'+str(l+1)] = parameters['b'+str(l+1)]-learning_rate*v['db'+str(l+1)]return parameters, v

测试一下

#测试update_parameters_with_momentun
print("-------------测试update_parameters_with_momentun-------------")
parameters,grads,v = testCase.update_parameters_with_momentum_test_case()
update_parameters_with_momentun(parameters,grads,v,beta=0.9,learning_rate=0.01)print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
print('v["dW1"] = ' + str(v["dW1"]))
print('v["db1"] = ' + str(v["db1"]))
print('v["dW2"] = ' + str(v["dW2"]))
print('v["db2"] = ' + str(v["db2"]))

-------------测试update_parameters_with_momentun-------------
W1 = [[ 1.62544598 -0.61290114 -0.52907334][-1.07347112  0.86450677 -2.30085497]]
b1 = [[ 1.74493465][-0.76027113]]
W2 = [[ 0.31930698 -0.24990073  1.4627996 ][-2.05974396 -0.32173003 -0.38320915][ 1.13444069 -1.0998786  -0.1713109 ]]
b2 = [[-0.87809283][ 0.04055394][ 0.58207317]]
v["dW1"] = [[-0.11006192  0.11447237  0.09015907][ 0.05024943  0.09008559 -0.06837279]]
v["db1"] = [[-0.01228902][-0.09357694]]
v["dW2"] = [[-0.02678881  0.05303555 -0.06916608][-0.03967535 -0.06871727 -0.08452056][-0.06712461 -0.00126646 -0.11173103]]
v["db2"] = [[0.02344157][0.16598022][0.07420442]]

需要注意的是速度v是用0来初始化的，因此，该算法需要经过几次迭代才能把速度提升上来并开始跨越更大步伐。当beta=0时，该算法相当于是没有使用momentum算法的标准的梯度下降算法。当beta越大的时候，说明平滑的作用越明显。通常0.9是比较合适的值。那如何才能在开始的时候就保持很快的速度向最小误差那里前进呢？我们来看看下面的Adam算法。

Adam算法

Adam算法是训练神经网络中最有效的算法之一，它是RMSProp算法与Momentum算法的结合体。我们来看看它都干了些什么吧~

 ??1. 计算以前的梯度的**指数加权平均值**，并将其存储在变量$v$（偏差校正前）和$v^{corrected}$(偏差校正后）中。2. 计算以前梯度的**平方的指数加权平均值**，并将其存储在变量$s$ （偏差校正前）和$s^{corrected}$（偏差校正后）中。3. 根据1和2更新参数。

初始化参数

def initialize_adam(parameters):'''初始化v和s，它们都是字典类型的变量，都包含了以下字段：- keys: "dW1", "db1", ..., "dWL", "dbL" - values：与对应的梯度/参数相同维度的值为零的numpy矩阵参数：parameters - 包含了以下参数的字典变量：parameters["W" + str(l)] = Wlparameters["b" + str(l)] = bl返回：v - 包含梯度的指数加权平均值，字段如下：v["dW" + str(l)] = ...v["db" + str(l)] = ...s - 包含平方梯度的指数加权平均值，字段如下：s["dW" + str(l)] = ...s["db" + str(l)] = ...'''L = len(parameters)//2  # 神经网络层数v = {
    }s = {
    }for l in range(L):# 计算梯度的指数加权平均值v['dW'+str(l+1)] = np.zeros_like(parameters['W'+str(l+1)])v['db'+str(l+1)] = np.zeros_like(parameters['b'+str(l+1)])# 计算梯度的平方的指数加权平均值s['dW'+str(l+1)] = np.zeros_like(parameters['W'+str(l+1)])s['db'+str(l+1)] = np.zeros_like(parameters['b'+str(l+1)])return (v, s)

测试一下

#测试initialize_adam
print("-------------测试initialize_adam-------------")
parameters = testCase.initialize_adam_test_case()
v,s = initialize_adam(parameters)print('v["dW1"] = ' + str(v["dW1"])) 
print('v["db1"] = ' + str(v["db1"])) 
print('v["dW2"] = ' + str(v["dW2"])) 
print('v["db2"] = ' + str(v["db2"])) 
print('s["dW1"] = ' + str(s["dW1"])) 
print('s["db1"] = ' + str(s["db1"])) 
print('s["dW2"] = ' + str(s["dW2"])) 
print('s["db2"] = ' + str(s["db2"])) 

-------------测试initialize_adam-------------
v["dW1"] = [[0. 0. 0.][0. 0. 0.]]
v["db1"] = [[0.][0.]]
v["dW2"] = [[0. 0. 0.][0. 0. 0.][0. 0. 0.]]
v["db2"] = [[0.][0.][0.]]
s["dW1"] = [[0. 0. 0.][0. 0. 0.]]
s["db1"] = [[0.][0.]]
s["dW2"] = [[0. 0. 0.][0. 0. 0.][0. 0. 0.]]
s["db2"] = [[0.][0.][0.]]

根据公式来更新参数：

def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate=0.01, beta1=0.9, beta2=0.999, epsilon=1e-8):'''使用Adam更新参数参数：parameters - 包含了以下字段的字典：parameters['W' + str(l)] = Wlparameters['b' + str(l)] = blgrads - 包含了梯度值的字典，有以下key值：grads['dW' + str(l)] = dWlgrads['db' + str(l)] = dblv - Adam的变量，第一个梯度的移动平均值，是一个字典类型的变量s - Adam的变量，平方梯度的移动平均值，是一个字典类型的变量t - 当前迭代的次数learning_rate - 学习率beta1 - 动量，超参数,用于第一阶段，使得曲线的Y值不从0开始（参见天气数据的那个图）beta2 - RMSprop的一个参数，超参数epsilon - 防止除零操作（分母为0）返回：parameters - 更新后的参数v - 第一个梯度的移动平均值，是一个字典类型的变量s - 平方梯度的移动平均值，是一个字典类型的变量'''L = len(parameters)//2v_corrected = {
    }  #偏差修正后的值s_corrected = {
    }  #偏差修正后的值for l in range(L):# 梯度的移动平均值# 输入：v，grads，beta1# 输出：vv['dW'+str(l+1)] = beta1*v['dW'+str(l+1)]+(1-beta1)*grads['dW'+str(l+1)]v['db'+str(l+1)] = beta1*v['db'+str(l+1)]+(1-beta1)*grads['db'+str(l+1)]# 计算第一阶段的偏差修正后的估计值# 输入：v，beta1，t# 输出：v_correctedv_corrected['dW'+str(l+1)] = v['dW'+str(l+1)] / (1-np.power(beta1, t))v_corrected['db'+str(l+1)] = v['db'+str(l+1)] / (1-np.power(beta1, t))# 计算平方梯度的移动平均值# 输入：s，grads，beta2# 输出：ss['dW'+str(l+1)] = beta2*s['dW'+str(l+1)]+(1-beta2)*np.square(grads['dW'+str(l+1)])s['db'+str(l+1)] = beta2*s['db'+str(l+1)]+(1-beta2)*np.square(grads['db'+str(l+1)])# 计算第二阶段的偏差修正后的估计值# 输入：s，beta2，t# 输出：s_correcteds_corrected['dW'+str(l+1)] = s['dW'+str(l+1)]/(1-np.power(beta2, t))s_corrected['db'+str(l+1)] = s['db'+str(l+1)]/(1-np.power(beta2, t))# 更新参数# 输入：parameters，learning_rate，v_corrected，s_corrected，epsilon# 输出：parametersparameters['W'+str(l+1)] = parameters['W'+str(l+1)]-learning_rate*(v_corrected['dW'+str(l+1)]/np.sqrt(s_corrected['dW'+str(l+1)]+epsilon))parameters['b'+str(l+1)] = parameters['b'+str(l+1)]-learning_rate*(v_corrected['db'+str(l+1)]/np.sqrt(s_corrected['db'+str(l+1)]+epsilon))return (parameters, v, s)

测试一下

#测试update_with_parameters_with_adam
print("-------------测试update_with_parameters_with_adam-------------")
parameters , grads , v , s = testCase.update_parameters_with_adam_test_case()
update_parameters_with_adam(parameters,grads,v,s,t=2)print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
print('v["dW1"] = ' + str(v["dW1"])) 
print('v["db1"] = ' + str(v["db1"])) 
print('v["dW2"] = ' + str(v["dW2"])) 
print('v["db2"] = ' + str(v["db2"])) 
print('s["dW1"] = ' + str(s["dW1"])) 
print('s["db1"] = ' + str(s["db1"])) 
print('s["dW2"] = ' + str(s["dW2"])) 
print('s["db2"] = ' + str(s["db2"])) 

-------------测试update_with_parameters_with_adam-------------
W1 = [[ 1.63178673 -0.61919778 -0.53561312][-1.08040999  0.85796626 -2.29409733]]
b1 = [[ 1.75225313][-0.75376553]]
W2 = [[ 0.32648046 -0.25681174  1.46954931][-2.05269934 -0.31497584 -0.37661299][ 1.14121081 -1.09245036 -0.16498684]]
b2 = [[-0.88529978][ 0.03477238][ 0.57537385]]
v["dW1"] = [[-0.11006192  0.11447237  0.09015907][ 0.05024943  0.09008559 -0.06837279]]
v["db1"] = [[-0.01228902][-0.09357694]]
v["dW2"] = [[-0.02678881  0.05303555 -0.06916608][-0.03967535 -0.06871727 -0.08452056][-0.06712461 -0.00126646 -0.11173103]]
v["db2"] = [[0.02344157][0.16598022][0.07420442]]
s["dW1"] = [[0.00121136 0.00131039 0.00081287][0.0002525  0.00081154 0.00046748]]
s["db1"] = [[1.51020075e-05][8.75664434e-04]]
s["dW2"] = [[7.17640232e-05 2.81276921e-04 4.78394595e-04][1.57413361e-04 4.72206320e-04 7.14372576e-04][4.50571368e-04 1.60392066e-07 1.24838242e-03]]
s["db2"] = [[5.49507194e-05][2.75494327e-03][5.50629536e-04]]

测试

在测试正式开始之前，我们需要把数据集加载进来。

加载数据集

我们使用下面的“月亮（moon）”数据集来测试不同的优化方法。数据集被命名为“月亮”，因为这两个类的数据看起来有点像新月形的月亮。

train_X, train_Y = opt_utils.load_dataset(is_plot=True)

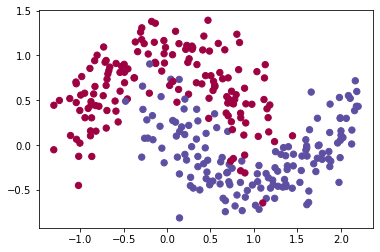
定义模型

def model(X, Y, layers_dims, optimizer, learning_rate=0.0007,mini_batch_size=64, beta=0.9, beta1=0.9, beta2=0.999,epsilon=1e-8, num_epochs=10000, print_cost=True, is_plot=True):"""可以运行在不同优化器模式下的3层神经网络模型。参数：X - 输入数据，维度为（2，输入的数据集里面样本数量）Y - 与X对应的标签layers_dims - 包含层数和节点数量的列表optimizer - 字符串类型的参数，用于选择优化类型，【 "gd" | "momentum" | "adam" 】learning_rate - 学习率mini_batch_size - 每个小批量数据集的大小beta - 用于动量优化的一个超参数beta1 - 用于计算梯度后的指数衰减的估计的超参数beta1 - 用于计算平方梯度后的指数衰减的估计的超参数epsilon - 用于在Adam中避免除零操作的超参数，一般不更改num_epochs - 整个训练集的遍历次数，（视频2.9学习率衰减，1分55秒处，视频中称作“代”）,相当于之前的num_iterationprint_cost - 是否打印误差值，每遍历1000次数据集打印一次，但是每100次记录一个误差值，又称每1000代打印一次is_plot - 是否绘制出曲线图返回：parameters - 包含了学习后的参数"""L = len(layers_dims)  # 神经网络层数costs = []  # 代价值t = 0 #每学习完一个minibatch就增加1seed = 10 #随机种子#初始化参数parameters = opt_utils.initialize_parameters(layers_dims)#选择优化器if optimizer == "gd":pass #不使用任何优化器，直接使用梯度下降法elif optimizer == "momentum":v = initialize_velocity(parameters) #使用动量elif optimizer == "adam":v, s = initialize_adam(parameters)#使用Adam优化else:print("optimizer参数错误，程序退出。")exit(1)#开始学习for i in range(num_epochs):#定义随机 minibatches,我们在每次遍历数据集之后增加种子以重新排列数据集，使每次数据的顺序都不同seed = seed + 1minibatches = random_mini_batches(X, Y, mini_batch_size, seed)for minibatch in minibatches:#选择一个minibatch(minibatch_X, minibatch_Y) = minibatch#前向传播 A3, cache = opt_utils.forward_propagation(minibatch_X,parameters)#计算误差cost = opt_utils.compute_cost(A3 , minibatch_Y)#反向传播grads = opt_utils.backward_propagation(minibatch_X,minibatch_Y,cache)#更新参数if optimizer == "gd":parameters = update_parameters_with_gd(parameters,grads,learning_rate)elif optimizer == "momentum":parameters, v = update_parameters_with_momentun(parameters,grads,v,beta,learning_rate)elif optimizer == "adam":t = t + 1 parameters , v , s = update_parameters_with_adam(parameters,grads,v,s,t,learning_rate,beta1,beta2,epsilon)#记录误差值if i % 100 == 0:costs.append(cost)#是否打印误差值if print_cost and i % 1000 == 0:print("第" + str(i) + "次遍历整个数据集，当前误差值：" + str(cost))#是否绘制曲线图if is_plot:plt.plot(costs)plt.ylabel('cost')plt.xlabel('epochs (per 100)')plt.title("Learning rate = " + str(learning_rate))plt.show()return parameters

梯度下降测试

#使用普通的梯度下降
layers_dims = [train_X.shape[0],5,2,1]
parameters = model(train_X, train_Y, layers_dims, optimizer="gd",is_plot=True)

第0次遍历整个数据集，当前误差值：0.690735512291113
第1000次遍历整个数据集，当前误差值：0.6852725328458241
第2000次遍历整个数据集，当前误差值：0.6470722240719003
第3000次遍历整个数据集，当前误差值：0.6195245549970403
第4000次遍历整个数据集，当前误差值：0.5765844355950944
第5000次遍历整个数据集，当前误差值：0.6072426395968576
第6000次遍历整个数据集，当前误差值：0.5294033317684576
第7000次遍历整个数据集，当前误差值：0.46076823985930115
第8000次遍历整个数据集，当前误差值：0.465586082399045
第9000次遍历整个数据集，当前误差值：0.46451797221676844

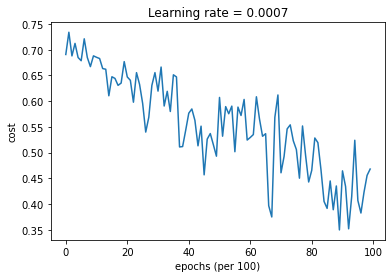
绘制分类的情况：

#预测
preditions = opt_utils.predict(train_X,train_Y,parameters)#绘制分类图
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5, 2.5])
axes.set_ylim([-1, 1.5])
opt_utils.plot_decision_boundary(lambda x: opt_utils.predict_dec(parameters, x.T), train_X, train_Y)

Accuracy: 0.7966666666666666

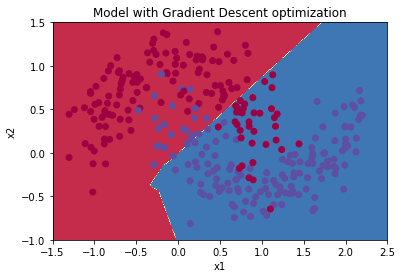
具有动量的梯度下降测试

layers_dims = [train_X.shape[0],5,2,1]
#使用动量的梯度下降
parameters = model(train_X, train_Y, layers_dims, beta=0.9,optimizer="momentum",is_plot=True)

第0次遍历整个数据集，当前误差值：0.6907412988351506
第1000次遍历整个数据集，当前误差值：0.6853405261267578
第2000次遍历整个数据集，当前误差值：0.6471448370095255
第3000次遍历整个数据集，当前误差值：0.6195943032076022
第4000次遍历整个数据集，当前误差值：0.5766650344073023
第5000次遍历整个数据集，当前误差值：0.607323821900647
第6000次遍历整个数据集，当前误差值：0.5294761758786996
第7000次遍历整个数据集，当前误差值：0.46093619004872366
第8000次遍历整个数据集，当前误差值：0.465780093701272
第9000次遍历整个数据集，当前误差值：0.4647395967922748

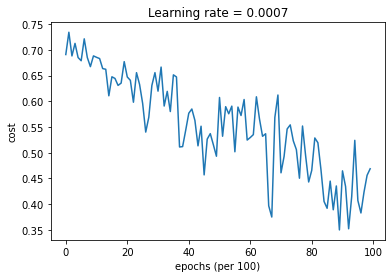
绘制分类的情况：

#预测
preditions = opt_utils.predict(train_X,train_Y,parameters)#绘制分类图
plt.title("Model with Momentum optimization")
axes = plt.gca()
axes.set_xlim([-1.5, 2.5])
axes.set_ylim([-1, 1.5])
opt_utils.plot_decision_boundary(lambda x: opt_utils.predict_dec(parameters, x.T), train_X, train_Y)

Accuracy: 0.7966666666666666

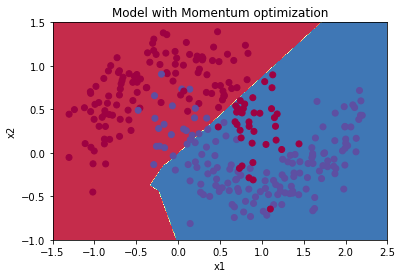
Adam优化后的梯度下降

layers_dims = [train_X.shape[0], 5, 2, 1]
#使用Adam优化的梯度下降
parameters = model(train_X, train_Y, layers_dims, optimizer="adam", is_plot=True)

第0次遍历整个数据集，当前误差值：0.6905522446113365
第1000次遍历整个数据集，当前误差值：0.18550136438550574
第2000次遍历整个数据集，当前误差值：0.150830465752532
第3000次遍历整个数据集，当前误差值：0.07445438570997183
第4000次遍历整个数据集，当前误差值：0.12595915651337164
第5000次遍历整个数据集，当前误差值：0.10434443534245487
第6000次遍历整个数据集，当前误差值：0.10067637504120643
第7000次遍历整个数据集，当前误差值：0.0316520301351156
第8000次遍历整个数据集，当前误差值：0.11197273131244204
第9000次遍历整个数据集，当前误差值：0.19794007152465481

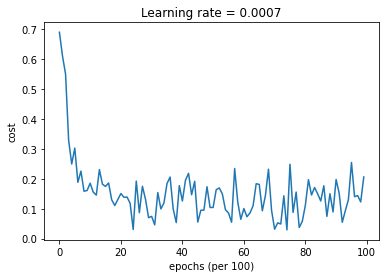
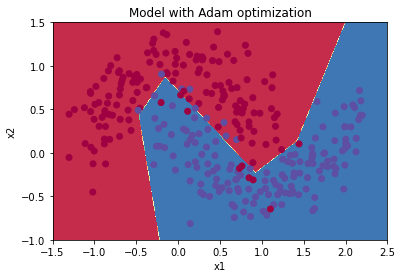
查看分类的效果图：

#预测
preditions = opt_utils.predict(train_X,train_Y,parameters)#绘制分类图
plt.title("Model with Adam optimization")
axes = plt.gca()
axes.set_xlim([-1.5, 2.5])
axes.set_ylim([-1, 1.5])
opt_utils.plot_decision_boundary(lambda x: opt_utils.predict_dec(parameters, x.T), train_X, train_Y)

Accuracy: 0.94

总结

优化算法	准确度	曲线平滑度
梯度下降	79.7%	震荡
具有动量的梯度下降算法	79.7%	震荡
Adam优化后的梯度下降	94%	平滑

具有动量的梯度下降通常可以有很好的效果，但由于小的学习速率和简单的数据集所以它的影响几乎是轻微的。另一方面，Adam明显优于小批量梯度下降和具有动量的梯度下降，如果在这个简单的模型上运行更多时间的数据集，这三种方法都会产生非常好的结果，然而，我们已经看到Adam收敛得更快。

Adam的一些优点包括相对较低的内存要求（虽然比梯度下降和动量下降更高）和通常运作良好，即使对参数进行微调（除了学习率$\alpha$）

相关库代码

opt_utils.py

# -*- coding: utf-8 -*-#opt_utils.pyimport numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasetsdef sigmoid(x):"""Compute the sigmoid of xArguments:x -- A scalar or numpy array of any size.Return:s -- sigmoid(x)"""s = 1/(1+np.exp(-x))return sdef relu(x):"""Compute the relu of xArguments:x -- A scalar or numpy array of any size.Return:s -- relu(x)"""s = np.maximum(0,x)return sdef load_params_and_grads(seed=1):np.random.seed(seed)W1 = np.random.randn(2,3)b1 = np.random.randn(2,1)W2 = np.random.randn(3,3)b2 = np.random.randn(3,1)dW1 = np.random.randn(2,3)db1 = np.random.randn(2,1)dW2 = np.random.randn(3,3)db2 = np.random.randn(3,1)return W1, b1, W2, b2, dW1, db1, dW2, db2def initialize_parameters(layer_dims):"""Arguments:layer_dims -- python array (list) containing the dimensions of each layer in our networkReturns:parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":W1 -- weight matrix of shape (layer_dims[l], layer_dims[l-1])b1 -- bias vector of shape (layer_dims[l], 1)Wl -- weight matrix of shape (layer_dims[l-1], layer_dims[l])bl -- bias vector of shape (1, layer_dims[l])Tips:- For example: the layer_dims for the "Planar Data classification model" would have been [2,2,1]. This means W1's shape was (2,2), b1 was (1,2), W2 was (2,1) and b2 was (1,1). Now you have to generalize it!- In the for loop, use parameters['W' + str(l)] to access Wl, where l is the iterative integer."""np.random.seed(3)parameters = {
    }L = len(layer_dims) # number of layers in the networkfor l in range(1, L):parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1])*  np.sqrt(2 / layer_dims[l-1])parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))assert(parameters['W' + str(l)].shape == layer_dims[l], layer_dims[l-1])assert(parameters['W' + str(l)].shape == layer_dims[l], 1)return parametersdef forward_propagation(X, parameters):"""Implements the forward propagation (and computes the loss) presented in Figure 2.Arguments:X -- input dataset, of shape (input size, number of examples)parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":W1 -- weight matrix of shape ()b1 -- bias vector of shape ()W2 -- weight matrix of shape ()b2 -- bias vector of shape ()W3 -- weight matrix of shape ()b3 -- bias vector of shape ()Returns:loss -- the loss function (vanilla logistic loss)"""# retrieve parametersW1 = parameters["W1"]b1 = parameters["b1"]W2 = parameters["W2"]b2 = parameters["b2"]W3 = parameters["W3"]b3 = parameters["b3"]# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOIDz1 = np.dot(W1, X) + b1a1 = relu(z1)z2 = np.dot(W2, a1) + b2a2 = relu(z2)z3 = np.dot(W3, a2) + b3a3 = sigmoid(z3)cache = (z1, a1, W1, b1, z2, a2, W2, b2, z3, a3, W3, b3)return a3, cachedef backward_propagation(X, Y, cache):"""Implement the backward propagation presented in figure 2.Arguments:X -- input dataset, of shape (input size, number of examples)Y -- true "label" vector (containing 0 if cat, 1 if non-cat)cache -- cache output from forward_propagation()Returns:gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables"""m = X.shape[1](z1, a1, W1, b1, z2, a2, W2, b2, z3, a3, W3, b3) = cachedz3 = 1./m * (a3 - Y)dW3 = np.dot(dz3, a2.T)db3 = np.sum(dz3, axis=1, keepdims = True)da2 = np.dot(W3.T, dz3)dz2 = np.multiply(da2, np.int64(a2 > 0))dW2 = np.dot(dz2, a1.T)db2 = np.sum(dz2, axis=1, keepdims = True)da1 = np.dot(W2.T, dz2)dz1 = np.multiply(da1, np.int64(a1 > 0))dW1 = np.dot(dz1, X.T)db1 = np.sum(dz1, axis=1, keepdims = True)gradients = {
    "dz3": dz3, "dW3": dW3, "db3": db3,"da2": da2, "dz2": dz2, "dW2": dW2, "db2": db2,"da1": da1, "dz1": dz1, "dW1": dW1, "db1": db1}return gradientsdef compute_cost(a3, Y):"""Implement the cost functionArguments:a3 -- post-activation, output of forward propagationY -- "true" labels vector, same shape as a3Returns:cost - value of the cost function"""m = Y.shape[1]logprobs = np.multiply(-np.log(a3),Y) + np.multiply(-np.log(1 - a3), 1 - Y)cost = 1./m * np.sum(logprobs)return costdef predict(X, y, parameters):"""This function is used to predict the results of a n-layer neural network.Arguments:X -- data set of examples you would like to labelparameters -- parameters of the trained modelReturns:p -- predictions for the given dataset X"""m = X.shape[1]p = np.zeros((1,m), dtype = np.int)# Forward propagationa3, caches = forward_propagation(X, parameters)# convert probas to 0/1 predictionsfor i in range(0, a3.shape[1]):if a3[0,i] > 0.5:p[0,i] = 1else:p[0,i] = 0# print results#print ("predictions: " + str(p[0,:]))#print ("true labels: " + str(y[0,:]))print("Accuracy: "  + str(np.mean((p[0,:] == y[0,:]))))return pdef predict_dec(parameters, X):"""Used for plotting decision boundary.Arguments:parameters -- python dictionary containing your parameters X -- input data of size (m, K)Returnspredictions -- vector of predictions of our model (red: 0 / blue: 1)"""# Predict using forward propagation and a classification threshold of 0.5a3, cache = forward_propagation(X, parameters)predictions = (a3 > 0.5)return predictionsdef plot_decision_boundary(model, X, y):# Set min and max values and give it some paddingx_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1h = 0.01# Generate a grid of points with distance h between themxx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))# Predict the function value for the whole gridZ = model(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)# Plot the contour and training examplesplt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)plt.ylabel('x2')plt.xlabel('x1')plt.scatter(X[0, :], X[1, :], c=y, cmap=plt.cm.Spectral)plt.show()def load_dataset(is_plot = True):np.random.seed(3)train_X, train_Y = sklearn.datasets.make_moons(n_samples=300, noise=.2) #300 #0.2 # Visualize the dataif is_plot:plt.scatter(train_X[:, 0], train_X[:, 1], c=train_Y, s=40, cmap=plt.cm.Spectral);train_X = train_X.Ttrain_Y = train_Y.reshape((1, train_Y.shape[0]))return train_X, train_Y

<>:78: SyntaxWarning: assertion is always true, perhaps remove parentheses?
<>:79: SyntaxWarning: assertion is always true, perhaps remove parentheses?
<>:78: SyntaxWarning: assertion is always true, perhaps remove parentheses?
<>:79: SyntaxWarning: assertion is always true, perhaps remove parentheses?
<>:78: SyntaxWarning: assertion is always true, perhaps remove parentheses?
<>:79: SyntaxWarning: assertion is always true, perhaps remove parentheses?
<ipython-input-34-e21589530eb6>:78: SyntaxWarning: assertion is always true, perhaps remove parentheses?assert(parameters['W' + str(l)].shape == layer_dims[l], layer_dims[l-1])
<ipython-input-34-e21589530eb6>:79: SyntaxWarning: assertion is always true, perhaps remove parentheses?assert(parameters['W' + str(l)].shape == layer_dims[l], 1)

testCase.py

# -*- coding: utf-8 -*-#testCase.pyimport numpy as npdef update_parameters_with_gd_test_case():np.random.seed(1)learning_rate = 0.01W1 = np.random.randn(2,3)b1 = np.random.randn(2,1)W2 = np.random.randn(3,3)b2 = np.random.randn(3,1)dW1 = np.random.randn(2,3)db1 = np.random.randn(2,1)dW2 = np.random.randn(3,3)db2 = np.random.randn(3,1)parameters = {
    "W1": W1, "b1": b1, "W2": W2, "b2": b2}grads = {
    "dW1": dW1, "db1": db1, "dW2": dW2, "db2": db2}return parameters, grads, learning_rate""" def update_parameters_with_sgd_checker(function, inputs, outputs):if function(inputs) == outputs:print("Correct")else:print("Incorrect") """def random_mini_batches_test_case():np.random.seed(1)mini_batch_size = 64X = np.random.randn(12288, 148)Y = np.random.randn(1, 148) < 0.5return X, Y, mini_batch_sizedef initialize_velocity_test_case():np.random.seed(1)W1 = np.random.randn(2,3)b1 = np.random.randn(2,1)W2 = np.random.randn(3,3)b2 = np.random.randn(3,1)parameters = {
    "W1": W1, "b1": b1, "W2": W2, "b2": b2}return parametersdef update_parameters_with_momentum_test_case():np.random.seed(1)W1 = np.random.randn(2,3)b1 = np.random.randn(2,1)W2 = np.random.randn(3,3)b2 = np.random.randn(3,1)dW1 = np.random.randn(2,3)db1 = np.random.randn(2,1)dW2 = np.random.randn(3,3)db2 = np.random.randn(3,1)parameters = {
    "W1": W1, "b1": b1, "W2": W2, "b2": b2}grads = {
    "dW1": dW1, "db1": db1, "dW2": dW2, "db2": db2}v = {
    'dW1': np.array([[ 0.,  0.,  0.],[ 0.,  0.,  0.]]), 'dW2': np.array([[ 0.,  0.,  0.],[ 0.,  0.,  0.],[ 0.,  0.,  0.]]), 'db1': np.array([[ 0.],[ 0.]]), 'db2': np.array([[ 0.],[ 0.],[ 0.]])}return parameters, grads, vdef initialize_adam_test_case():np.random.seed(1)W1 = np.random.randn(2,3)b1 = np.random.randn(2,1)W2 = np.random.randn(3,3)b2 = np.random.randn(3,1)parameters = {
    "W1": W1, "b1": b1, "W2": W2, "b2": b2}return parametersdef update_parameters_with_adam_test_case():np.random.seed(1)v, s = ({
    'dW1': np.array([[ 0.,  0.,  0.],[ 0.,  0.,  0.]]), 'dW2': np.array([[ 0.,  0.,  0.],[ 0.,  0.,  0.],[ 0.,  0.,  0.]]), 'db1': np.array([[ 0.],[ 0.]]), 'db2': np.array([[ 0.],[ 0.],[ 0.]])}, {
    'dW1': np.array([[ 0.,  0.,  0.],[ 0.,  0.,  0.]]), 'dW2': np.array([[ 0.,  0.,  0.],[ 0.,  0.,  0.],[ 0.,  0.,  0.]]), 'db1': np.array([[ 0.],[ 0.]]), 'db2': np.array([[ 0.],[ 0.],[ 0.]])})W1 = np.random.randn(2,3)b1 = np.random.randn(2,1)W2 = np.random.randn(3,3)b2 = np.random.randn(3,1)dW1 = np.random.randn(2,3)db1 = np.random.randn(2,1)dW2 = np.random.randn(3,3)db2 = np.random.randn(3,1)parameters = {
    "W1": W1, "b1": b1, "W2": W2, "b2": b2}grads = {
    "dW1": dW1, "db1": db1, "dW2": dW2, "db2": db2}return parameters, grads, v, s