进阶篇---Soft Actor-Critic (SAC)

进阶篇—Soft Actor-Critic (SAC)

SAC是一个off-policy + actor critic + maximum entropy的RL算法。比DDPG，SVG等方法稳定并且效果更好。代码参见我的GitHub

前言

1、on-policy 与 off-policy：
on-policy：“边交互边学习” ，每一次参数更新时，都需要与环境交互，因而当遇到复杂任务时，需要的更新步骤更多，增大了复杂度
off-policy ：“重用过去的经验”，典型的就是经验池策略的方法，比如DQN，DDPG中使用的都是这种方法，但是问题在于稳定性和收敛性较差。
2、最大化熵
学过信息论的同学可能对这个概念并不陌生，不过这里仍然简单介绍一下。
熵是衡量不确定性的一种表达形式，对于一个确定发生的事情，比如某个动作发生的概率是1，那么此时我们认为其熵为0. 很显然，这种情况是及其不利于我们学习的，我们希望所有动作出现的概率尽可能的相等，这样初始条件下agent可以有最大的探索能力。当动作空间中的所有动作发生概率相等，即均匀分布时，我们认为此时熵为1.
因此，最大化熵有以下两个好处：
a)、鼓励exploration
b)、可以学到更多near-optimal的行为，也就是在一些状态下，可能存在多个动作都是最优的，那么使选择它们的概率相同，可以提高学习的速度

算法理论

SAC的方法结合了三点：
1、Actor-critic框架（用两个网络分别近似policy和value function／Q function）
2、Off-policy（提高样本效率）
3、最大化entropy（熵）来保证稳定性和exploration

Soft Policy Iteration

soft policy lteration 是一种用于学习最大熵策略的通用算法，通过迭代交替使用policy evaluation和policy improvement得到最终策略
1、policy evaluation step
传统的最大熵强化学习的优化目标为

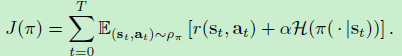
因此，我们希望通过上式来计算策略$\pi$的值。而对于一个固定的策略，soft Q-value可以通过迭代的方法来计算，即：

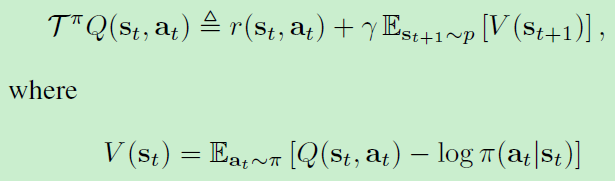
其中$T^{\pi }$是Bellman backup 算子，满足$Q^{k+1}=T^{\pi }{Q}^k$ 。对于任意策略$\pi$,我们可以重复使用$T^{\pi }$来获得最终的soft state value function $V(s_t)$.
2、policy improvement step
在policy improvement中，按照下式进行更新

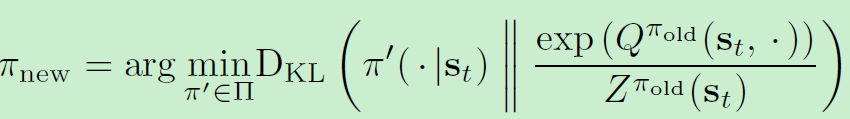
其中partition function $Z^{{\pi }_{old}}$正则化分布，同时其与策略梯度无关

Soft Actor-Critic

基于soft policy lteration， 我们用神经网络去近似soft Q-function和policy也能比较好的收敛性质（神经网络近似的方法能解决更高维问题）


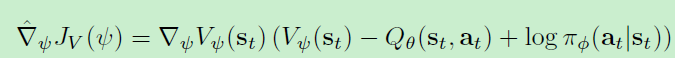
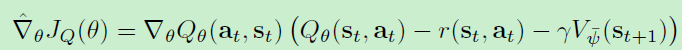
更新中使用来target网络以切断相关性


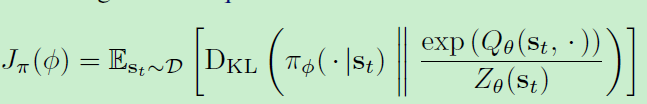
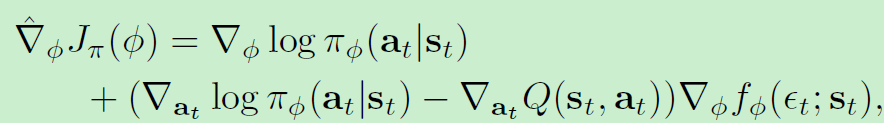
最终算法为

运行结果