文章主要提出了连续卷积算子操作，用一个隐式插值模型来形成一个在连续空间上的学习问题。下图中第一张图表示的是多分辨率的特征图，第二张图表示的是学习到的连续卷积算子，第三张图表示的是每层的置信分数，最后一张表示的是合并后的分数图，得到目标位置。
学习连续卷积算子
(1)首先，在一维空间上介绍文章中的学习方法，然后在扩展到图片的二维空间上去。
g:R→C是在空间L2(T)上的以T为周期，Lebesgue可积的复数函数。L2(T)空间是一个带有内积运算的Hilbert空间。对于在空间L2(T)上的函数g和h，他们的内积和卷积定义公式如下图所示。
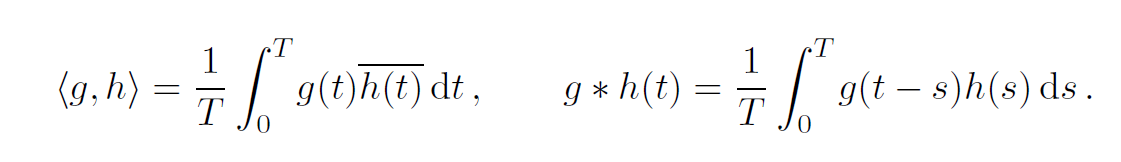
其中，横线代表复共轭。在上面的公式中，右面的就是循环卷积操作，得到的数也是在空间L2(T)上的。
用复指数函数ekt=ei2πTkt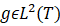
作为上面公式的h(t)。定义傅里叶系数g?L2(T)
g的傅里叶序列就是
傅里叶系数满足Parseval公式
|
傅里叶系数满足下面的操作
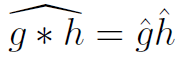
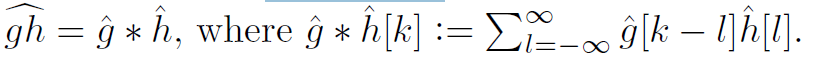
(2)连续学习方法
学习的目的是基于训练样本xj训练一个连续的卷积操作。样本包括了从图片块提取到的特征图。每个样本xj包含了D个通道的特征图
，都来自于同一个图片块。传统的DCF算法假设所有的通道的特征图有相同的空间分辨率和相同数量的空间采样点。文章提出的方法消除了这种限制，令Nd表示第d个通道特征图的空间采样点数目（分辨率）。xjd?RNd可以被看做一个被离散空间变量
作为角标的函数
。样本空间可以被描述成
为了提出连续空间域的学习问题，作者最训练样本引入了一个隐形插值模型。作者把连续的间隔[0,T)当作特征图的空间支持。标量T表示支持区域的尺寸。实际上，T是任意的，因为它代表了坐标系的缩放。对于每一个特征通道d，定义插值运算：
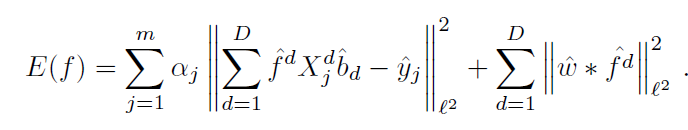
插值样本
是一个插值函数
移位后的累加和。在上面的公式中，特征值
就是每个移位函数的权重。和传统的离散DCF计算的周期假设类似，特征图的周期扩展也被计算出来。
目标是学习一个线性卷积操作
。这个操作将一个属于X的样本x放到了一个目标置信函数
中，这个函数在连续域[0,T)上定义。其中，s(t)?R是图片上位置t的置信分数。和离散的判别方法一样，通过在图像区域内找到最大的置信分数就可以得到目标的位置。文章中的方法不同的地方在于置信分数是连续的不是离散的，所以目标可以定位到亚像素上，更精确。
在连续域上的计算中，算子
被一系列的卷积滤波器
参数化。其中，fd∈L2(T)是d通道特征的卷积滤波器。可以定义卷积运算公式：
这里，每个特征通道首先被插值运算，然后被相关滤波卷积。注意的是，这里的卷积操作是在连续域上进行的。最后，所有的卷积后的响应相加起来，得到最后的置信分数。
在标注你的DCF算法中，每个训练样本被离散的函数打标签来表示期望的卷积后的输出。相反，文章的样本xj是在连续域上打标签，
。损失函数可以表示为：
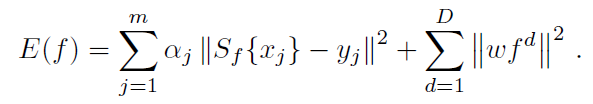
(3)训练滤波器
为了训练滤波器f，需要在频域上最小化E(f)这个公式。Sf{x}可以进行傅里叶变换，写成下面的形式：
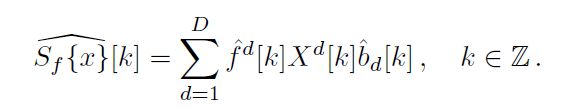
E(f)函数可以改写成：
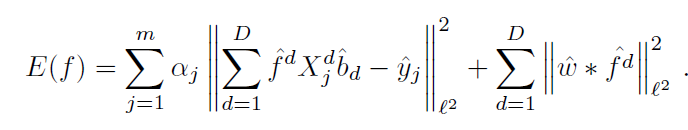
通过求解这个方程，可以求得滤波器。
目标跟踪框架
（1）目标定位
首先得到图片中的感兴趣区域的特征图。用之前的公式求出置信分数函数s=Sf{x}
的傅里叶系数，然后计算出频域上的分数。分两步去在连续域[0,T）上最大化分数s(t)。
1.首先进行网格搜索，得分函数在离散的位置上s(Tn2K+1)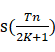
去计算相应的分数，找到最大值，作为迭代优化的初始值。
2.把上一步获得的最大值作为傅里叶展开迭代优化的初始值，用标准的牛顿方法去优化。
（2）框架
1. 从预训练好的深度网络中提取出多分辨率特征图；
2. 每帧中提取单个训练样本，从以目标位置为中心的图像区域提取样本，并将区域大小设置为目标框区域的25倍(可以调节)。
3.采用多尺度搜索。
4.目标定位。
5.求解滤波器。
实验
