参考文献ensemble-learning
1.导言
本章我们继续讨论集成学习方法的最后一个成员–Stacking,这个集成方法在比赛中被称为“懒人”算法,因为它不需要花费过多时间的调参就可以得到一个效果不错的算法,同时,这种算法也比前两种算法容易理解的多,因为这种集成学习的方式不需要理解太多的理论,只需要在实际中加以运用即可。 stacking严格来说并不是一种算法,而是精美而又复杂的,对模型集成的一种策略。 Stacking集成算法可以理解为一个两层的集成,第一层含有多个基础分类器,把预测的结果(元特征)提供给第二层, 而第二层的分类器通常是逻辑回归,他把一层分类器的结果当做特征做拟合输出预测结果。在介绍Stacking之前,我们先来对简化版的Stacking进行讨论,也叫做Blending,接着我们对Stacking进行更深入的讨论。
2. Blending集成学习算法
不知道大家小时候有没有过这种经历:老师上课提问到你,那时候你因为开小差而无法立刻得知问题的答案。就在你彷徨的时候,由于你平时人缘比较好,因此周围的同学向你伸出援手告诉了你他们脑中的正确答案,因此你对他们的答案加以总结和分析最终的得出正确答案。 相信大家都有过这样的经历,说这个故事的目的是为了引出集成学习家族中的Blending方式,这种集成方式跟我们的故事是十分相像的。如图:(图片来源:https://blog.csdn.net/maqunfi/article/details/82220115)
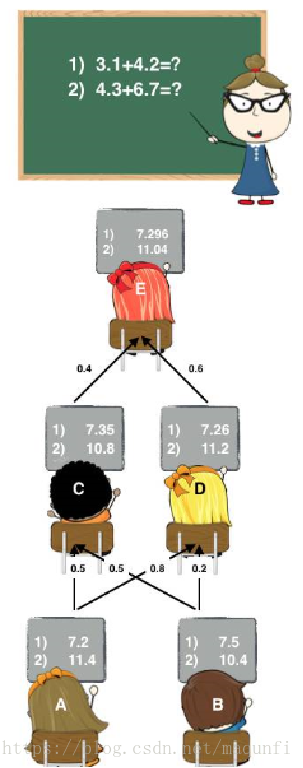
下面我们来详细讨论下这个Blending集成学习方式:
- (1) 将数据划分为训练集和测试集(test_set),其中训练集需要再次划分为训练集(train_set)和验证集(val_set);
- (2) 创建第一层的多个模型,这些模型可以使同质的也可以是异质的;
- (3) 使用train_set训练步骤2中的多个模型,然后用训练好的模型预测 val_set和 test_set得到val_predict, test_predict1;
- (4) 创建第二层的模型,使用val_predict作为训练集训练第二层的模型;
- (5) 使用第二层训练好的模型对第二层测试集test_predict1进行预测,该结果为整个测试集的结果。
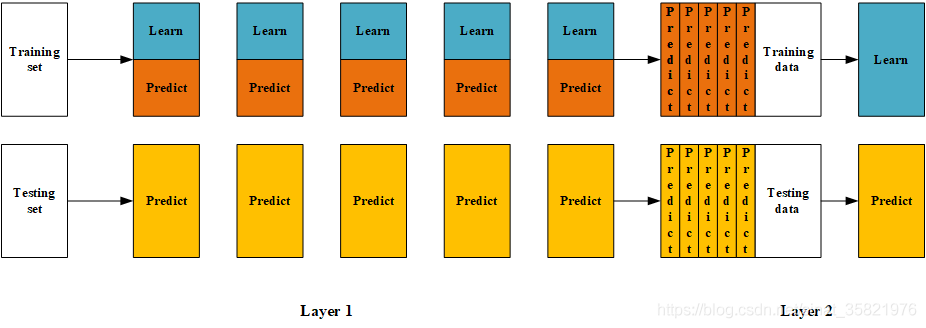
在这里,笔者先来梳理下这个过程:
在(1)步中,总的数据集被分成训练集和测试集,如80%训练集和20%测试集,然后在这80%的训练集中再拆分训练集70%和验证集30%,因此拆分后的数据集由三部分组成:训练集80%* 70%
、测试集20%、验证集80%* 30% 。训练集是为了训练模型,测试集是为了调整模型(调参),测试集则是为了检验模型的优度。
在(2)-(3)步中,我们使用训练集创建了K个模型,如SVM、random forests、XGBoost等,这个是第一层的模型。 训练好模型后将验证集输入模型进行预测,得到K组不同的输出,我们记作A1,...,AKA_1,...,A_KA1?,...,AK?,然后将测试集输入K个模型也得到K组输出,我们记作B1,...,BKB_1,...,B_KB1?,...,BK?,其中AiA_iAi?的样本数与验证集一致,BiB_iBi?的样本数与测试集一致。如果总的样本数有10000个样本,那么使用5600个样本训练了K个模型,输入验证集2400个样本得到K组2400个样本的结果A1,...,AKA_1,...,A_KA1?,...,AK?,输入测试集2000个得到K组2000个样本的结果B1,...,BKB_1,...,B_KB1?,...,BK? 。
在(4)步中,我们使用K组2400个样本的验证集结果A1,...,AKA_1,...,A_KA1?,...,AK?作为第二层分类器的特征,验证集的2400个标签为因变量,训练第二层分类器,得到2400个样本的输出。
在(5)步中,将输入测试集2000个得到K组2000个样本的结果B1,...,BKB_1,...,B_KB1?,...,BK?放入第二层分类器,得到2000个测试集的预测结果。
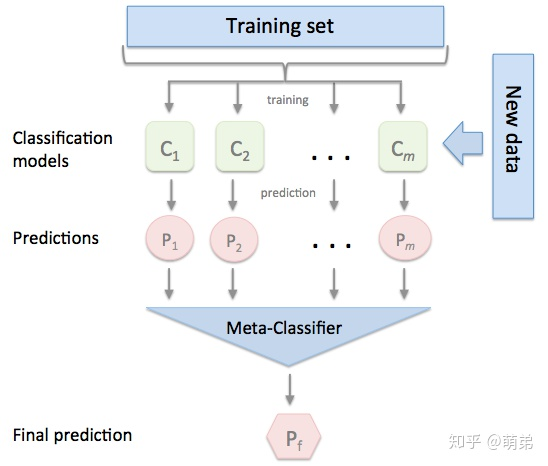
以上是Blending集成方式的过程,接下来我们来分析这个集成方式的优劣:
其中一个最重要的优点就是实现简单粗暴,没有太多的理论的分析。但是这个方法的缺点也是显然的:blending只使用了一部分数据集作为留出集进行验证,也就是只能用上数据中的一部分,实际上这对数据来说是很奢侈浪费的。
关于这个缺点,我们以后再做改进,我们先来用一些案例来使用这个集成方式。
# 加载相关工具包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.style.use("ggplot")
%matplotlib inline
import seaborn as sns
# 创建数据
from sklearn import datasets
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
data, target = make_blobs(n_samples=10000, centers=2, random_state=1, cluster_std=1.0 )
## 创建训练集和测试集
X_train1,X_test,y_train1,y_test = train_test_split(data, target, test_size=0.2, random_state=1)
## 创建训练集和验证集
X_train,X_val,y_train,y_val = train_test_split(X_train1, y_train1, test_size=0.3, random_state=1)
print("The shape of training X:",X_train.shape)
print("The shape of training y:",y_train.shape)
print("The shape of test X:",X_test.shape)
print("The shape of test y:",y_test.shape)
print("The shape of validation X:",X_val.shape)
print("The shape of validation y:",y_val.shape)
The shape of training X: (5600, 2)
The shape of training y: (5600,)
The shape of test X: (2000, 2)
The shape of test y: (2000,)
The shape of validation X: (2400, 2)
The shape of validation y: (2400,)
# 设置第一层分类器
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifierclfs = [SVC(probability = True),RandomForestClassifier(n_estimators=5, n_jobs=-1, criterion='gini'),KNeighborsClassifier()]# 设置第二层分类器
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
# 输出第一层的验证集结果与测试集结果
val_features = np.zeros((X_val.shape[0],len(clfs))) # 初始化验证集结果
test_features = np.zeros((X_test.shape[0],len(clfs))) # 初始化测试集结果for i,clf in enumerate(clfs):clf.fit(X_train,y_train)val_feature = clf.predict_proba(X_val)[:, 1]test_feature = clf.predict_proba(X_test)[:,1]val_features[:,i] = val_featuretest_features[:,i] = test_feature# 将第一层的验证集的结果输入第二层训练第二层分类器
lr.fit(val_features,y_val)
# 输出预测的结果
from sklearn.model_selection import cross_val_score
cross_val_score(lr,test_features,y_test,cv=5)
array([1., 1., 1., 1., 1.])
可以看到,在每一折的交叉验证的效果都是非常好的,这个集成学习方法在这个数据集上是十分有效的,不过这个数据集是我们虚拟的,因此大家可以把他用在实际数据上看看效果
3. Stacking集成学习算法
基于前面对Blending集成学习算法的讨论,我们知道:Blending在集成的过程中只会用到验证集的数据,对数据实际上是一个很大的浪费。为了解决这个问题,我们详细分析下Blending到底哪里出现问题并如何改进。在Blending中,我们产生验证集的方式是使用分割的方式,产生一组训练集和一组验证集,这让我们联想到交叉验证的方式。顺着这个思路,我们对Stacking进行建模(如下图):
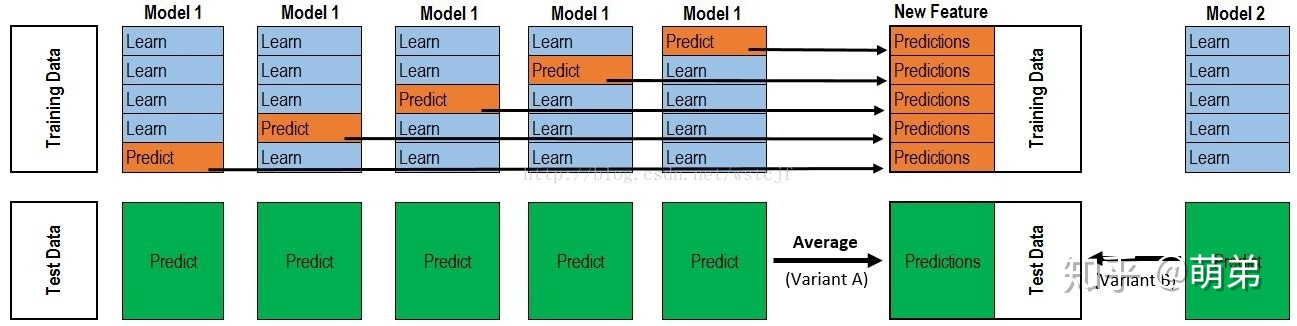
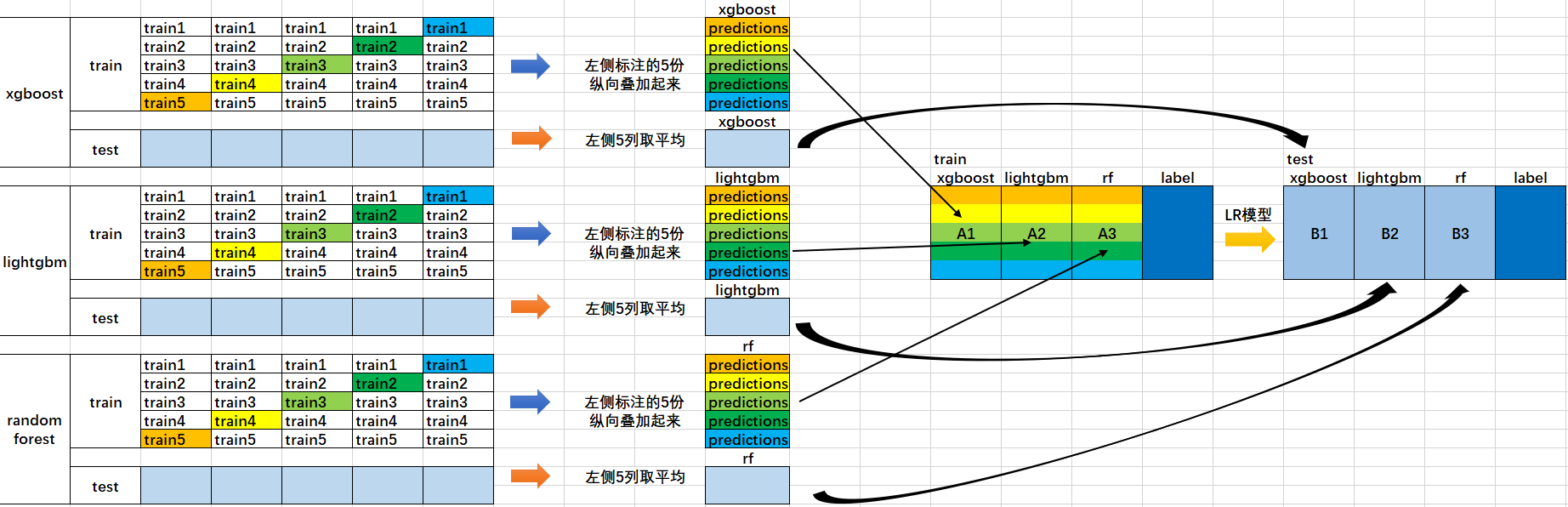
- 首先将所有数据集生成测试集和训练集(假如训练集为10000,测试集为2500行),那么上层会进行5折交叉检验,使用训练集中的8000条作为训练集,剩余2000行作为验证集(橙色)。
- 每次验证相当于使用了蓝色的8000条数据训练出一个模型,使用模型对验证集进行验证得到2000条数据,并对测试集进行预测,得到2500条数据,这样经过5次交叉检验,可以得到中间的橙色的5* 2000条验证集的结果(相当于每条数据的预测结果),5* 2500条测试集的预测结果。
- 接下来会将验证集的5* 2000条预测结果拼接成10000行长的矩阵,标记为A1A_1A1?,而对于5* 2500行的测试集的预测结果进行加权平均,得到一个2500一列的矩阵,标记为B1B_1B1?。
- 上面得到一个基模型在数据集上的预测结果A1A_1A1?、B1B_1B1?,这样当我们对3个基模型进行集成的话,相于得到了A1A_1A1?、A2A_2A2?、A3A_3A3?、B1B_1B1?、B2B_2B2?、B3B_3B3?六个矩阵。
- 之后我们会将A1A_1A1?、A2A_2A2?、A3A_3A3?并列在一起成10000行3列的矩阵作为training data,B1B_1B1?、B2B_2B2?、B3B_3B3?合并在一起成2500行3列的矩阵作为testing data,让下层学习器基于这样的数据进行再训练。
- 再训练是基于每个基础模型的预测结果作为特征(三个特征),次学习器会学习训练如果往这样的基学习的预测结果上赋予权重w,来使得最后的预测最为准确。
下面,我们来实际应用下Stacking是如何集成算法的:(参考案例:https://www.cnblogs.com/Christina-Notebook/p/10063146.html)
由于sklearn并没有直接对Stacking的方法,因此我们需要下载mlxtend工具包(pip install mlxtend)
1. 简单堆叠3折CV分类
from sklearn import datasetsiris = datasets.load_iris()
X, y = iris.data[:, 1:3], iris.target
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from mlxtend.classifier import StackingCVClassifierRANDOM_SEED = 42clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=RANDOM_SEED)
clf3 = GaussianNB()
lr = LogisticRegression()# Starting from v0.16.0, StackingCVRegressor supports
# `random_state` to get deterministic result.
sclf = StackingCVClassifier(classifiers=[clf1, clf2, clf3], # 第一层分类器meta_classifier=lr, # 第二层分类器random_state=RANDOM_SEED)print('3-fold cross validation:\n')for clf, label in zip([clf1, clf2, clf3, sclf], ['KNN', 'Random Forest', 'Naive Bayes','StackingClassifier']):scores = cross_val_score(clf, X, y, cv=3, scoring='accuracy')print("Accuracy: %0.2f (+/- %0.2f) [%s]" % (scores.mean(), scores.std(), label))
3-fold cross validation:
Accuracy: 0.91 (+/- 0.01) [KNN]
Accuracy: 0.95 (+/- 0.01) [Random Forest]
Accuracy: 0.91 (+/- 0.02) [Naive Bayes]
Accuracy: 0.93 (+/- 0.02) [StackingClassifier]
# 我们画出决策边界
from mlxtend.plotting import plot_decision_regions
import matplotlib.gridspec as gridspec
import itertoolsgs = gridspec.GridSpec(2, 2)
fig = plt.figure(figsize=(10,8))
for clf, lab, grd in zip([clf1, clf2, clf3, sclf], ['KNN', 'Random Forest', 'Naive Bayes','StackingCVClassifier'],itertools.product([0, 1], repeat=2)):clf.fit(X, y)ax = plt.subplot(gs[grd[0], grd[1]])fig = plot_decision_regions(X=X, y=y, clf=clf)plt.title(lab)
plt.show()
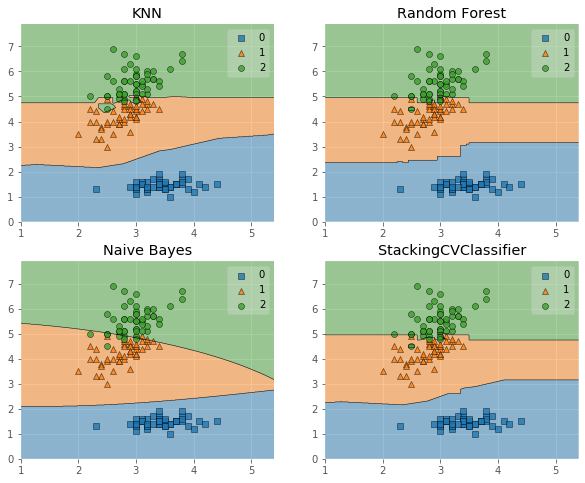
使用第一层所有基分类器所产生的类别概率值作为meta-classfier的输入。需要在StackingClassifier 中增加一个参数设置:use_probas = True。
另外,还有一个参数设置average_probas = True,那么这些基分类器所产出的概率值将按照列被平均,否则会拼接。
例如:
基分类器1:predictions=[0.2,0.2,0.7]
基分类器2:predictions=[0.4,0.3,0.8]
基分类器3:predictions=[0.1,0.4,0.6]
1)若use_probas = True,average_probas = True,
则产生的meta-feature 为:[0.233, 0.3, 0.7]
2)若use_probas = True,average_probas = False,
则产生的meta-feature 为:0.2,0.2,0.7,0.4,0.3,0.8,0.1,0.4,0.6]
2.使用概率作为元特征 use_probas=True
clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=1)
clf3 = GaussianNB()
lr = LogisticRegression()sclf = StackingCVClassifier(classifiers=[clf1, clf2, clf3],use_probas=True, # 2.使用概率作为元特征meta_classifier=lr,random_state=42)print('3-fold cross validation:\n')for clf, label in zip([clf1, clf2, clf3, sclf], ['KNN', 'Random Forest', 'Naive Bayes','StackingClassifier']):scores = cross_val_score(clf, X, y, cv=3, scoring='accuracy')print("Accuracy: %0.2f (+/- %0.2f) [%s]" % (scores.mean(), scores.std(), label))
3-fold cross validation:
Accuracy: 0.91 (+/- 0.01) [KNN]
Accuracy: 0.95 (+/- 0.01) [Random Forest]
Accuracy: 0.91 (+/- 0.02) [Naive Bayes]
Accuracy: 0.95 (+/- 0.02) [StackingClassifier]
3. 堆叠5折CV分类与网格搜索(结合网格搜索调参优化)
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
from mlxtend.classifier import StackingCVClassifier# Initializing modelsclf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=RANDOM_SEED)
clf3 = GaussianNB()
lr = LogisticRegression()sclf = StackingCVClassifier(classifiers=[clf1, clf2, clf3], meta_classifier=lr,random_state=42)params = {
'kneighborsclassifier__n_neighbors': [1, 5],'randomforestclassifier__n_estimators': [10, 50],'meta_classifier__C': [0.1, 10.0]}grid = GridSearchCV(estimator=sclf, param_grid=params, cv=5,refit=True)
grid.fit(X, y)cv_keys = ('mean_test_score', 'std_test_score', 'params')for r, _ in enumerate(grid.cv_results_['mean_test_score']):print("%0.3f +/- %0.2f %r"% (grid.cv_results_[cv_keys[0]][r],grid.cv_results_[cv_keys[1]][r] / 2.0,grid.cv_results_[cv_keys[2]][r]))print('Best parameters: %s' % grid.best_params_)
print('Accuracy: %.2f' % grid.best_score_)
0.947 +/- 0.03 {‘kneighborsclassifier__n_neighbors’: 1, ‘meta_classifier__C’: 0.1, ‘randomforestclassifier__n_estimators’: 10}
0.933 +/- 0.02 {‘kneighborsclassifier__n_neighbors’: 1, ‘meta_classifier__C’: 0.1, ‘randomforestclassifier__n_estimators’: 50}
0.940 +/- 0.02 {‘kneighborsclassifier__n_neighbors’: 1, ‘meta_classifier__C’: 10.0, ‘randomforestclassifier__n_estimators’: 10}
0.940 +/- 0.02 {‘kneighborsclassifier__n_neighbors’: 1, ‘meta_classifier__C’: 10.0, ‘randomforestclassifier__n_estimators’: 50}
0.953 +/- 0.02 {‘kneighborsclassifier__n_neighbors’: 5, ‘meta_classifier__C’: 0.1, ‘randomforestclassifier__n_estimators’: 10}
0.953 +/- 0.02 {‘kneighborsclassifier__n_neighbors’: 5, ‘meta_classifier__C’: 0.1, ‘randomforestclassifier__n_estimators’: 50}
0.953 +/- 0.02 {‘kneighborsclassifier__n_neighbors’: 5, ‘meta_classifier__C’: 10.0, ‘randomforestclassifier__n_estimators’: 10}
0.953 +/- 0.02 {‘kneighborsclassifier__n_neighbors’: 5, ‘meta_classifier__C’: 10.0, ‘randomforestclassifier__n_estimators’: 50}
Best parameters: {‘kneighborsclassifier__n_neighbors’: 5, ‘meta_classifier__C’: 0.1, ‘randomforestclassifier__n_estimators’: 10}
Accuracy: 0.95
# 如果我们打算多次使用回归算法,我们要做的就是在参数网格中添加一个附加的数字后缀,如下所示:
from sklearn.model_selection import GridSearchCV# Initializing modelsclf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=RANDOM_SEED)
clf3 = GaussianNB()
lr = LogisticRegression()sclf = StackingCVClassifier(classifiers=[clf1, clf1, clf2, clf3], meta_classifier=lr,random_state=RANDOM_SEED)params = {
'kneighborsclassifier-1__n_neighbors': [1, 5],'kneighborsclassifier-2__n_neighbors': [1, 5],'randomforestclassifier__n_estimators': [10, 50],'meta_classifier__C': [0.1, 10.0]}grid = GridSearchCV(estimator=sclf, param_grid=params, cv=5,refit=True)
grid.fit(X, y)cv_keys = ('mean_test_score', 'std_test_score', 'params')for r, _ in enumerate(grid.cv_results_['mean_test_score']):print("%0.3f +/- %0.2f %r"% (grid.cv_results_[cv_keys[0]][r],grid.cv_results_[cv_keys[1]][r] / 2.0,grid.cv_results_[cv_keys[2]][r]))print('Best parameters: %s' % grid.best_params_)
print('Accuracy: %.2f' % grid.best_score_)
0.940 +/- 0.02 {‘kneighborsclassifier-1__n_neighbors’: 1, ‘kneighborsclassifier-2__n_neighbors’: 1, ‘meta_classifier__C’: 0.1, ‘randomforestclassifier__n_estimators’: 10}
0.940 +/- 0.02 {‘kneighborsclassifier-1__n_neighbors’: 1, ‘kneighborsclassifier-2__n_neighbors’: 1, ‘meta_classifier__C’: 0.1, ‘randomforestclassifier__n_estimators’: 50}
0.940 +/- 0.02 {‘kneighborsclassifier-1__n_neighbors’: 1, ‘kneighborsclassifier-2__n_neighbors’: 1, ‘meta_classifier__C’: 10.0, ‘randomforestclassifier__n_estimators’: 10}
0.940 +/- 0.02 {‘kneighborsclassifier-1__n_neighbors’: 1, ‘kneighborsclassifier-2__n_neighbors’: 1, ‘meta_classifier__C’: 10.0, ‘randomforestclassifier__n_estimators’: 50}
0.960 +/- 0.02 {‘kneighborsclassifier-1__n_neighbors’: 1, ‘kneighborsclassifier-2__n_neighbors’: 5, ‘meta_classifier__C’: 0.1, ‘randomforestclassifier__n_estimators’: 10}
0.953 +/- 0.02 {‘kneighborsclassifier-1__n_neighbors’: 1, ‘kneighborsclassifier-2__n_neighbors’: 5, ‘meta_classifier__C’: 0.1, ‘randomforestclassifier__n_estimators’: 50}
0.953 +/- 0.02 {‘kneighborsclassifier-1__n_neighbors’: 1, ‘kneighborsclassifier-2__n_neighbors’: 5, ‘meta_classifier__C’: 10.0, ‘randomforestclassifier__n_estimators’: 10}
0.953 +/- 0.02 {‘kneighborsclassifier-1__n_neighbors’: 1, ‘kneighborsclassifier-2__n_neighbors’: 5, ‘meta_classifier__C’: 10.0, ‘randomforestclassifier__n_estimators’: 50}
0.960 +/- 0.02 {‘kneighborsclassifier-1__n_neighbors’: 5, ‘kneighborsclassifier-2__n_neighbors’: 1, ‘meta_classifier__C’: 0.1, ‘randomforestclassifier__n_estimators’: 10}
0.953 +/- 0.02 {‘kneighborsclassifier-1__n_neighbors’: 5, ‘kneighborsclassifier-2__n_neighbors’: 1, ‘meta_classifier__C’: 0.1, ‘randomforestclassifier__n_estimators’: 50}
0.953 +/- 0.02 {‘kneighborsclassifier-1__n_neighbors’: 5, ‘kneighborsclassifier-2__n_neighbors’: 1, ‘meta_classifier__C’: 10.0, ‘randomforestclassifier__n_estimators’: 10}
0.953 +/- 0.02 {‘kneighborsclassifier-1__n_neighbors’: 5, ‘kneighborsclassifier-2__n_neighbors’: 1, ‘meta_classifier__C’: 10.0, ‘randomforestclassifier__n_estimators’: 50}
0.953 +/- 0.02 {‘kneighborsclassifier-1__n_neighbors’: 5, ‘kneighborsclassifier-2__n_neighbors’: 5, ‘meta_classifier__C’: 0.1, ‘randomforestclassifier__n_estimators’: 10}
0.953 +/- 0.02 {‘kneighborsclassifier-1__n_neighbors’: 5, ‘kneighborsclassifier-2__n_neighbors’: 5, ‘meta_classifier__C’: 0.1, ‘randomforestclassifier__n_estimators’: 50}
0.953 +/- 0.02 {‘kneighborsclassifier-1__n_neighbors’: 5, ‘kneighborsclassifier-2__n_neighbors’: 5, ‘meta_classifier__C’: 10.0, ‘randomforestclassifier__n_estimators’: 10}
0.953 +/- 0.02 {‘kneighborsclassifier-1__n_neighbors’: 5, ‘kneighborsclassifier-2__n_neighbors’: 5, ‘meta_classifier__C’: 10.0, ‘randomforestclassifier__n_estimators’: 50}
Best parameters: {‘kneighborsclassifier-1__n_neighbors’: 1, ‘kneighborsclassifier-2__n_neighbors’: 5, ‘meta_classifier__C’: 0.1, ‘randomforestclassifier__n_estimators’: 10}
Accuracy: 0.96
4.在不同特征子集上运行的分类器的堆叠
##不同的1级分类器可以适合训练数据集中的不同特征子集。以下示例说明了如何使用scikit-learn管道和ColumnSelector:
from sklearn.datasets import load_iris
from mlxtend.classifier import StackingCVClassifier
from mlxtend.feature_selection import ColumnSelector
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LogisticRegressioniris = load_iris()
X = iris.data
y = iris.targetpipe1 = make_pipeline(ColumnSelector(cols=(0, 2)), # 选择第0,2列LogisticRegression())
pipe2 = make_pipeline(ColumnSelector(cols=(1, 2, 3)), # 选择第1,2,3列LogisticRegression())sclf = StackingCVClassifier(classifiers=[pipe1, pipe2], meta_classifier=LogisticRegression(),random_state=42)sclf.fit(X, y)
StackingCVClassifier(classifiers=[Pipeline(steps=[(‘columnselector’,
ColumnSelector(cols=(0, 2))),
(‘logisticregression’,
LogisticRegression())]),
Pipeline(steps=[(‘columnselector’,
ColumnSelector(cols=(1, 2,
3))),
(‘logisticregression’,
LogisticRegression())])],
meta_classifier=LogisticRegression(), random_state=42)
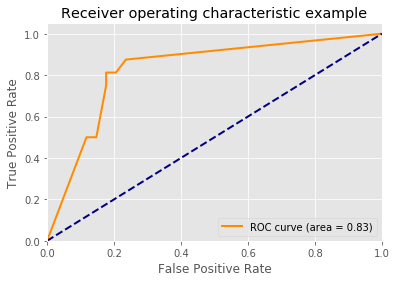
5.ROC曲线 decision_function
### 像其他scikit-learn分类器一样,它StackingCVClassifier具有decision_function可用于绘制ROC曲线的方法。
### 请注意,decision_function期望并要求元分类器实现decision_function。
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
from mlxtend.classifier import StackingCVClassifier
from sklearn.metrics import roc_curve, auc
from sklearn.model_selection import train_test_split
from sklearn import datasets
from sklearn.preprocessing import label_binarize
from sklearn.multiclass import OneVsRestClassifieriris = datasets.load_iris()
X, y = iris.data[:, [0, 1]], iris.target# Binarize the output
y = label_binarize(y, classes=[0, 1, 2])
n_classes = y.shape[1]RANDOM_SEED = 42X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=RANDOM_SEED)clf1 = LogisticRegression()
clf2 = RandomForestClassifier(random_state=RANDOM_SEED)
clf3 = SVC(random_state=RANDOM_SEED)
lr = LogisticRegression()sclf = StackingCVClassifier(classifiers=[clf1, clf2, clf3],meta_classifier=lr)# Learn to predict each class against the other
classifier = OneVsRestClassifier(sclf)
y_score = classifier.fit(X_train, y_train).decision_function(X_test)# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_score[:, i])roc_auc[i] = auc(fpr[i], tpr[i])# Compute micro-average ROC curve and ROC area
fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), y_score.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])plt.figure()
lw = 2
plt.plot(fpr[2], tpr[2], color='darkorange',lw=lw, label='ROC curve (area = %0.2f)' % roc_auc[2])
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()
Blending与Stacking对比:
Blending的优点在于:
- 比stacking简单(因为不用进行k次的交叉验证来获得stacker feature)
而缺点在于:
- 使用了很少的数据(是划分hold-out作为测试集,并非cv)
- blender可能会过拟合(其实大概率是第一点导致的)
- stacking使用多次的CV会比较稳健