（一）PyTorch 中的基本概念_计算图与动态图机制_综合

参考

本章代码：https://github.com/zhangxiann/PyTorch_Practice/blob/master/lesson1/computational_graph.py

计算图

深度学习就是对张量进行一系列的操作，随着操作种类和数量的增多，会出现各种值得思考的问题。比如多个操作之间是否可以并行，如何协同底层的不同设备，如何避免冗余的操作，以实现最高效的计算效率，同时避免一些 bug。因此产生了计算图 (Computational Graph)。
计算图是用来描述运算的有向无环图，有两个主要元素：节点 (Node) 和边 (Edge)。节点表示数据，如向量、矩阵、张量。边表示运算，如加减乘除卷积等。
用计算图表示： $y = (x + w) ? (w + 1)$ ，如下所示：
在这里插入图片描述
可以看作， $\times b$ ，其中 $a = x + w$ ， $b = w + 1$ 。
计算图与梯度求导
这里求 $y$ 对 $w$ 的导数。根复合函数的求导法则，可以得到如下过程。
$?y?w=?y?a?a?w+?y?b?b?w=b1+a1=b+a=(w+1)+(x+w)=2w+x+1=21+2+1=5\begin{aligned} \frac{\partial y}{\partial w} &=\frac{\partial y}{\partial a} \frac{\partial a}{\partial w}+\frac{\partial y}{\partial b} \frac{\partial b}{\partial w} \ &=b 1+a 1 \ &=b+a \ &=(w+1)+(x+w) \ &=2 w+x+1 \ &=2 1+2+1=5\end{aligned}$

体现到计算图中，就是根节点 $y$ 到叶子节点 $w$ 有两条路径 y -> a -> w和y ->b -> w。根节点依次对每条路径的孩子节点求导，一直到叶子节点w，最后把每条路径的导数相加即可。

在这里插入图片描述

import torch
w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
# y=(x+w)*(w+1)
a = torch.add(w, x)     # retain_grad()
b = torch.add(w, 1)
y = torch.mul(a, b)
# y 求导
y.backward()
# 打印 w 的梯度，就是 y 对 w 的导数
print(w.grad)

结果为tensor([5.])

我们回顾前面说过的 Tensor 中有一个属性is_leaf标记是否为叶子节点。
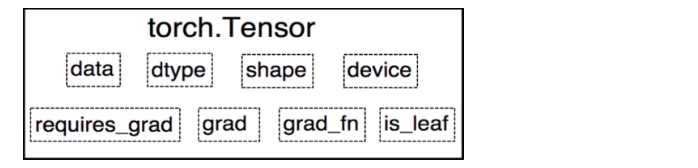
在这里插入图片描述
在上面的例子中， $x$ 和 $w$ 是叶子节点，其他所有节点都依赖于叶子节点。叶子节点的概念主要是为了节省内存，在计算图中的一轮反向传播结束之后，非叶子节点的梯度是会被释放的。
代码示例：

# 查看叶子结点
print("is_leaf:\n", w.is_leaf, x.is_leaf, a.is_leaf, b.is_leaf, y.is_leaf)# 查看梯度
print("gradient:\n", w.grad, x.grad, a.grad, b.grad, y.grad)

结果为：

is_leaf:True True False False False
gradient:tensor([5.]) tensor([2.]) None None None

非叶子节点的梯度为空，如果在反向传播结束之后仍然需要保留非叶子节点的梯度，可以对节点使用retain_grad()方法。

而 Tensor 中的 grad_fn 属性记录的是创建该张量时所用的方法 (函数)。而在反向传播求导梯度时需要用到该属性。
示例代码：

# 查看梯度
print("w.grad_fn = ", w.grad_fn)
print("x.grad_fn = ", x.grad_fn)
print("a.grad_fn = ", a.grad_fn)
print("b.grad_fn = ", b.grad_fn)
print("y.grad_fn = ", y.grad_fn)

结果为：

w.grad_fn =  None
x.grad_fn =  None
a.grad_fn =  <AddBackward0 object at 0x000001D8DDD20588>
b.grad_fn =  <AddBackward0 object at 0x000001D8DDD20588>
y.grad_fn =  <MulBackward0 object at 0x000001D8DDD20588>

PyTorch 的动态图机制

PyTorch 采用的是动态图机制 (Dynamic Computational Graph)，而 Tensorflow 采用的是静态图机制 (Static Computational Graph)。

动态图是运算和搭建同时进行，也就是可以先计算前面的节点的值，再根据这些值搭建后面的计算图。优点是灵活，易调节，易调试。PyTorch 里的很多写法跟其他 Python 库的代码的使用方法是完全一致的，没有任何额外的学习成本。

静态图是先搭建图，然后再输入数据进行运算。优点是高效，因为静态计算是通过先定义后运行的方式，之后再次运行的时候就不再需要重新构建计算图，所以速度会比动态图更快。但是不灵活。TensorFlow 每次运行的时候图都是一样的，是不能够改变的，所以不能直接使用 Python 的 while 循环语句，需要使用辅助函数 tf.while_loop 写成 TensorFlow 内部的形式。