1.面临问题:
人群计数在计算视觉领域很重要但是也很困难的问题。在图像上基于密度图估计的卷积网络在这个领域取得了巨大的成功。然而,密集的人群计数仍然是一个开放的问题,因为严重的遮挡和透视图中,人们可以出现在不同的大小。在这项工作中,使用ResNet做特征提取,提出一种新的网络,下采样使用空洞卷积(dilated convolutions),上采样模块使用反卷积( transposed convolutions)。我们提出了一个聚合模块,使得我们的网络在透视图问题(perspective view problem)上具有鲁棒性。我们展示了优化的细节,损失函数和算法在我们工作中的使用。使用MSE和MAE做为评价指标,在ShanghaiTech,UCF-CC-50和UCF-QNRF数据集评价。我们的方法达到最优然当用有原则的贝叶斯方法给出不确定性估计。
2.本文贡献:
本文主要贡献总结如下:
1、 我们基于ResNet做特征提取器提出了一个新的模型结构,下采样部分使用空洞卷积层,上采样部分使用反卷积层。
2、 我们展示了层级的细节,一个新的聚合模块,优化细节,损失函数,评估度量和算法在本项工作中的使用。
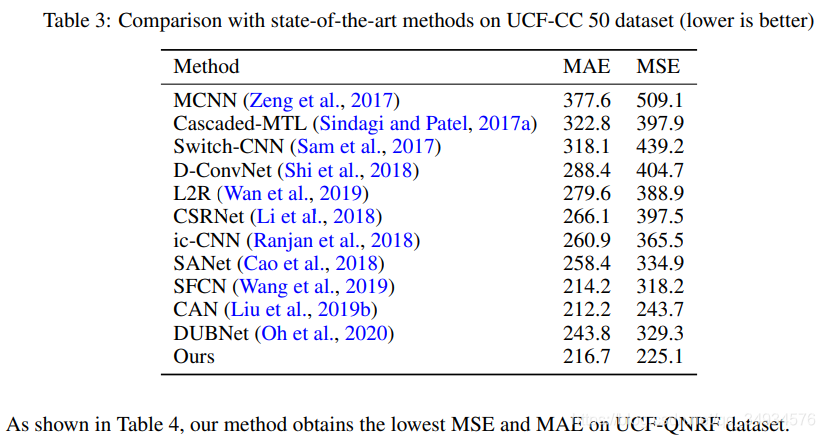
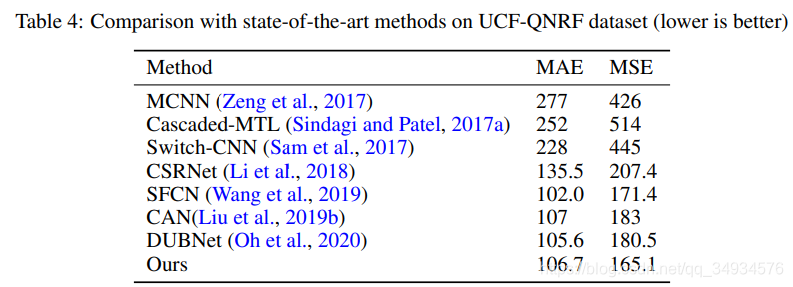
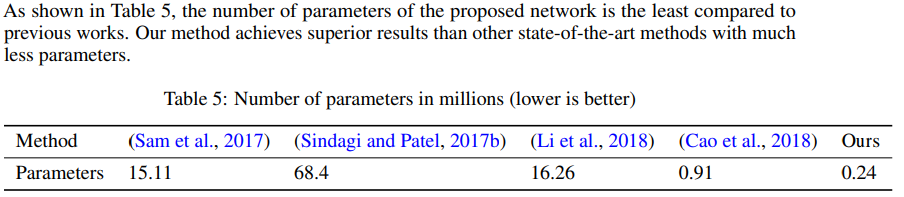
3、 在ShanghaiTech,UCF-CC-50和UCF-QNRF数据集使用MAE和MSE作为评价度量方式,我们的模型使用更小的参数量在性能上达到最优。
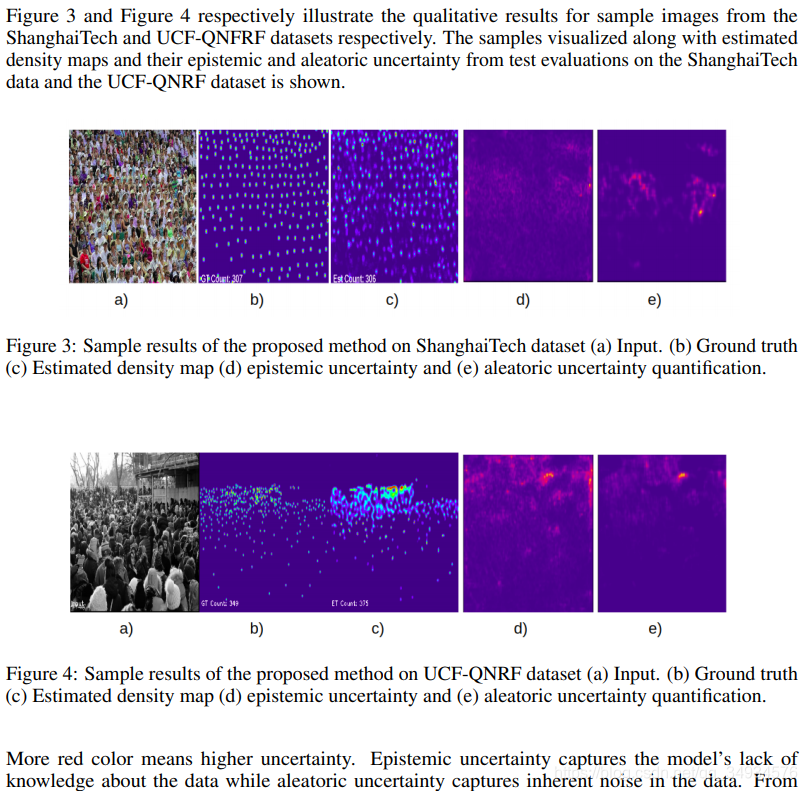
4、我们的网络在给出图像中出现的人数的同时,也给出了认知不确定性和任意不确定性的量化。
3.本文方法:
3.1数据集
评估实验使用的是三个公开的人群计数数据ShanghaiTech,UCF-CC-50和UCF-QNRF,这些数据集的描述如下:

3.2 模型结构

该网络结构由一个基于ResNet的特征提取器和使用空洞卷积定义的下采样模块组成。这有助于提取不同尺度下物体的细节,从而解决早期方法所面临的透视问题(perspective view problem)。接下来,上行采样块使用反卷积,并在两者之间跳过连接,从而创建一个额外的路径。
最后的一部分有三个头部:密度图的输出,当积分时给出绝对计数;认知不确定性(epistemic uncertainty)头部;任意不确定性(aleatoric uncertainty)头部。
3.3优化
在对网络进行训练时,出现了连接的【ie】权值为零的消失梯度问题。为了解决这个问题,在卷积和反卷积中使用IN(instance normalization)。定义如公式(1):

先前的一些工作为了处理物体可能出现在图像中的各种尺度,使用多列的网络结构。这些方法的问题在于,列的数量直接衡量了它识别单个对象的尺度。为了解决这个(To tackle this),我们提出了一种新的计数去融合1X1,3X3,5X5这些尺度上的filters。在每个卷积层和反卷积层后使用ReLU激活。这个filter分支使得我们的网络具有鲁棒性并且可以使用更多的filter去扩展来处理密集场景中的人群计数。我们的聚合模块堆叠在彼此之上,表现得像一个整体,从而最大限度地减少深度网络的过度拟合问题。我们工作中使用的新型聚合模块Figure2所示:
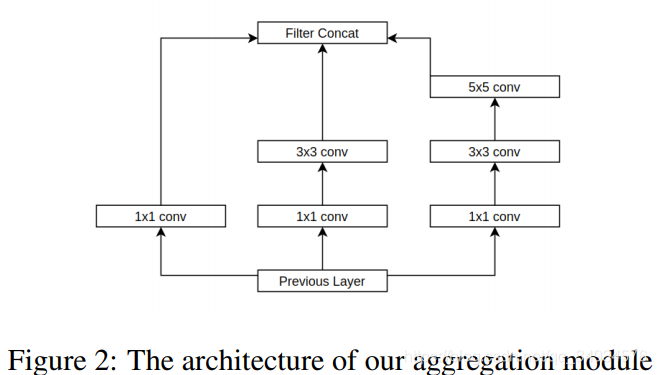

3.4损失函数
大多数现有的工作使用像素级的Euclidean loss训练网络。这给出了一个像素级估计误差的度量,定义在Equation2中。
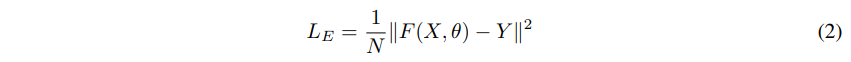

我们还在损失中加入了SSIM指数,以衡量预测与真实情况的偏差。图像质量评价采用SSIM指数。它通过三种局部统计量,即均值、方差和协方差来计算两幅图像之间的相似性。SSIM值从-1到1,当两幅图像相同时,SSIM值等于1。Equation 3定义了SSIM指数


3.5评估
对于人群计数,计数误差有两个度量标准,平均绝对误差(MAE,Mean Absolute Error)和均方误差(MSE,Mean Squared Error)。
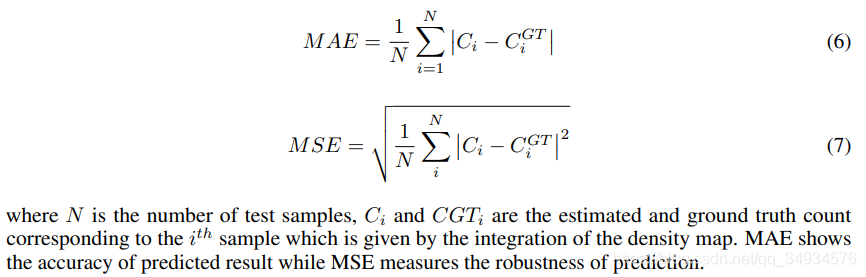
3.6不确定性估计(Uncertainty Estimation)
模型预测的不确定性主要有两个来源:认知的不确定性(epistemic uncertainty)是由于我们缺乏知识而产生的不确定性,而任意的不确定性(aleatoric uncertainty)是由于数据中存在的随机性。认知的不确定性通常被称为模型的不确定性,给足够的数据就可以解释它。利用贝叶斯神经网络,将权值参数化为分布而不是点估计,可以计算出认知的不确定性。
然而,人群计数需要理解数据的内在细微差别,如遮挡、尺度模糊等,因此任意的不确定性也很重要。为了在神经网络中捕捉认知的不确定性,我们将先验分布置于其权重之上。考虑到这一点,不确定性可以估计使用损失函数定义在Equation8,其中的目标是最小化负对数似然(negative log likelihood)。

3.7算法


4.实验结果:
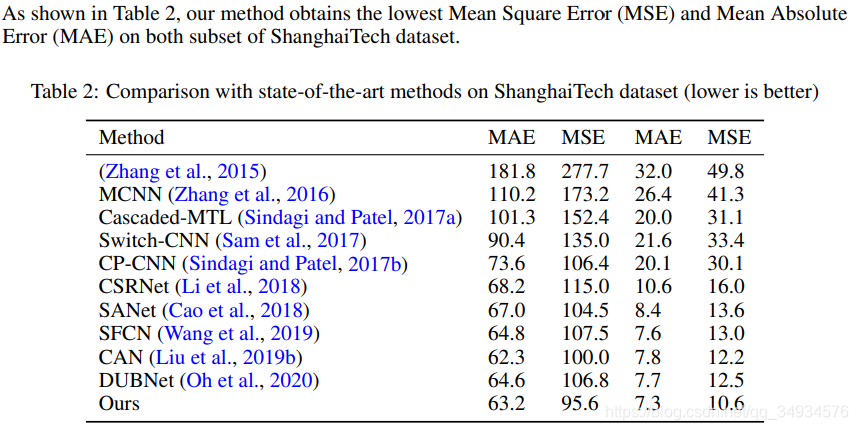

总结:
在本文中,我们提出了一种基于ResNet的特征提取器和一种新的特征聚合模块的人群计数网络。下行采样块使用空洞卷积层,上采样使用反卷积层。跳过块之间的连接可以创建额外的路径,从而防止过拟合。我们显示优化细节,损失函数和算法在这工作中使用。我们的方法在使用MSE和MAE作为评价指标的3个公开数据集上优于现有最优的方法。我们的方法也给出了一个不确定性度量,从而解决了神经网络的黑箱问题。