D. Pave the Parallelepiped
D题做法实际上很显然,你只要保证你选出来的三个数a,b,c能和A,B,C一一对应(这里的对应是指前者是后者的因子),但是由于A,B,C这三个数有可能有共同的因子。那么在选择的时候需要进行容斥来排除重复选择的情况。然而容斥很麻烦。。
其实我们不用想的那么复杂,首先我们可以画一幅图。
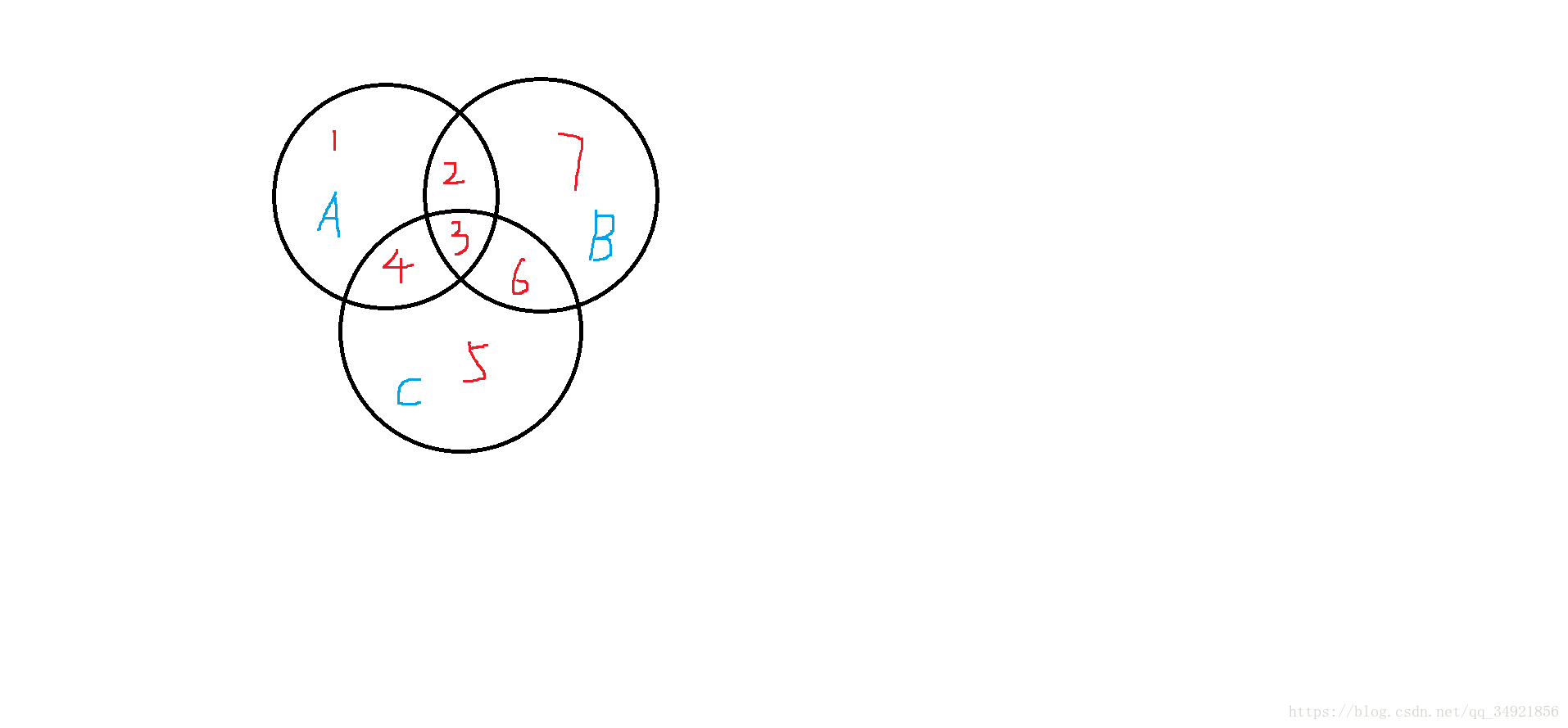
因子的种类实际上可以分成图上7类,你只要挑出3类,A,B,C都包括一类即可,怎么挑枚举一下即可。
假设现在挑出来的是a,b,c,那么当a!=b&&a!=c ans+=num[a]*num[b]*num[c].当a==b&&a!=c这里就需要排列组合一下,也不是很难。当a=b=c时也需要特别考虑,这不是难点。
所以这道题只需要预处理出能挑出来的3类的各个情况,那么接下来就好办了。
#include<bits/stdc++.h>
using namespace std;struct node
{int a,b,c;node(int _a,int _b,int _c):a(_a),b(_b),c(_c){if(a>b)swap(a,b);if(a>c)swap(a,c);if(b>c)swap(b,c);}node(){}bool operator<(const node&x)const{if(a!=x.a)return a<x.a;else{if(b!=x.b)return b<x.b;elsereturn c<x.c;}}
};
set<node>S;
int x[5]={
1,2,3,4};
int y[5]={
2,3,6,7};
int z[5]={
3,4,5,6};void init()
{for(int i=0;i<4;i++)for(int j=0;j<4;j++)for(int k=0;k<4;k++){node a=node(x[i],y[j],z[k]);S.insert(a);}//cout<<S.size()<<endl;
}int gcd(int a,int b)
{return b==0?a:gcd(b,a%b);
}
int num[10];int getfac(int num)
{int e=sqrt(num);int res=0;for(int i=1;i<=e;i++)if(num%i==0){res++;if(num/i!=i)res++;}return res;
}int main()
{init();int T;scanf("%d",&T);while(T--){memset(num,0,sizeof(num));int A,B,C;scanf("%d %d %d",&A,&B,&C);int tmp1=gcd(A,B);int tmp2=gcd(A,C);int tmp3=gcd(B,C);int tmp4=gcd(tmp1,C);num[3]=getfac(tmp4);num[2]=getfac(tmp1)-num[3];num[4]=getfac(tmp2)-num[3];num[6]=getfac(tmp3)-num[3];num[1]=getfac(A)-num[2]-num[3]-num[4];num[7]=getfac(B)-num[2]-num[3]-num[6];num[5]=getfac(C)-num[3]-num[4]-num[6];long long ans=0;for(auto itor=S.begin();itor!=S.end();itor++){int aidx=itor->a,bidx=itor->b,cidx=itor->c;if(aidx==bidx&&aidx==cidx){int tmp=num[aidx];ans+=1LL*tmp+(1LL*tmp*(tmp-1))+(1LL*tmp*(tmp-1)*(tmp-2))/6;}else if(aidx==bidx){int tmp=num[aidx];ans+=1LL*num[cidx]*(tmp+1LL*tmp*(tmp-1)/2);}else if(aidx==cidx){int tmp=num[aidx];ans+=1LL*num[bidx]*(tmp+1LL*tmp*(tmp-1)/2);}else if(bidx==cidx){int tmp=num[bidx];ans+=1LL*num[aidx]*(tmp+1LL*tmp*(tmp-1)/2);}elseans+=1LL*num[aidx]*num[bidx]*num[cidx];}printf("%lld\n",ans);}}