hdu多校第八场题解(=100人)

这场之前打过了，开虚拟比赛就偷懒了一下，搞了几天今天才把题补完呜呜呜。。
感觉题目都挺好的。
A - Character Encoding
这个当时做的时候想了很久，以为是母函数。将所求的转换成式子就为$(1+x^1+x^2+...+x^{n-1})^m$ 的k次幂的系数。
那么将它用等比数列求和公式表示后，再用牛顿二项式定理展开成组合数形式，那么问题就迎刃而解了。

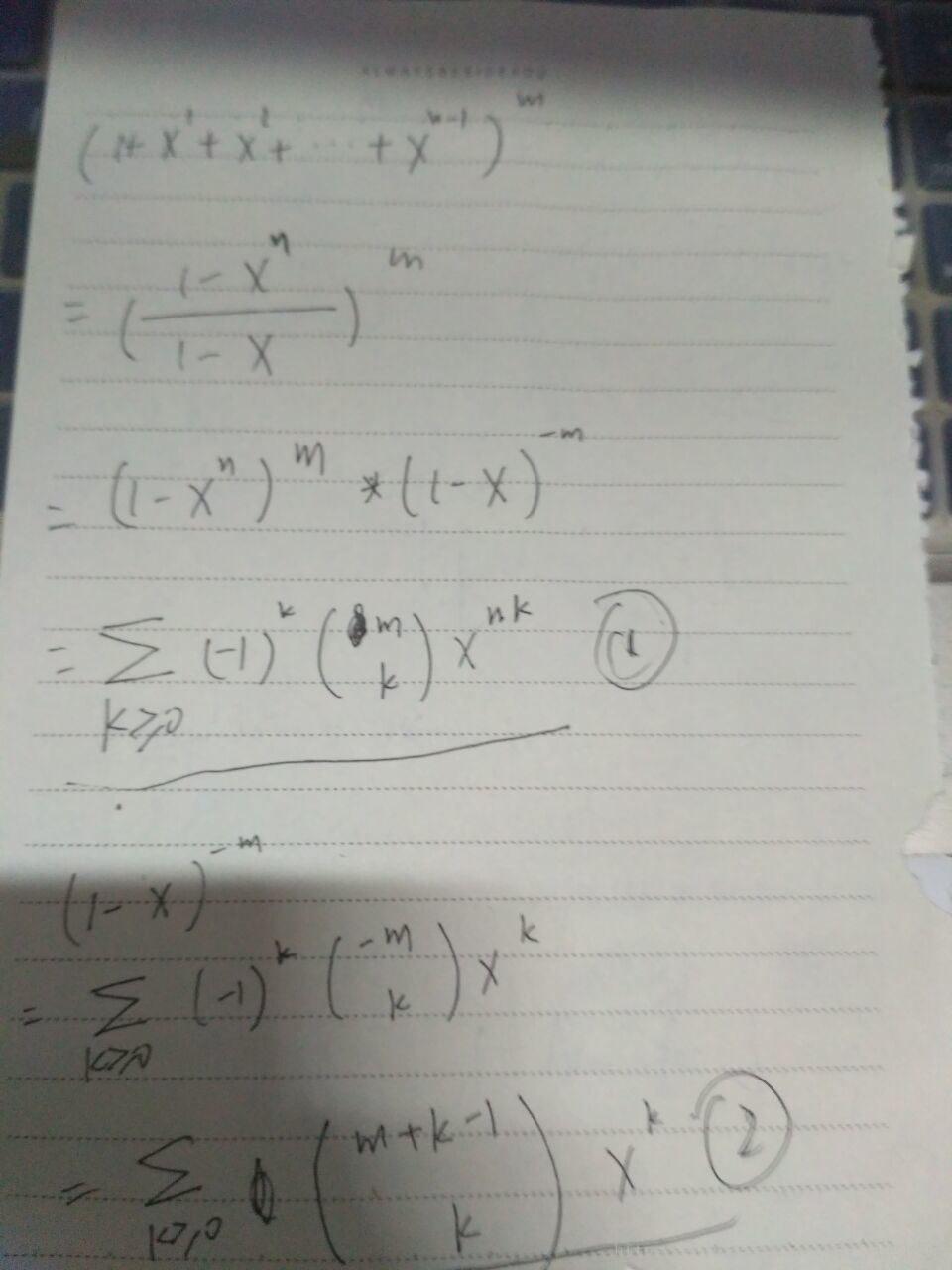
#include<bits/stdc++.h>
using namespace std;const int maxn=2e5+5;
const int mod=998244353;
//返回d=gcd(a,b)；和对应于等式ax+by=d中的x，y
long long extgcd(long long a,long long b,long long &x,long long &y)
{if(a==0&&b==0)return -1;//无最大公约数if(b==0){x=1;y=0;return a;}long long d=extgcd(b,a%b,y,x);y-=a/b*x;return d;//返回gcd(a,b)
}
//****************求逆元******************************
//ax=1(mod n)
long long mod_reverse(long long a,long long n)
{long long x,y;long long d=extgcd(a,n,x,y);if(d==1)return (x%n+n)%n;return -1;
}long long tab1[maxn],tab2[maxn];
void init()
{tab1[0]=1;for(int i=1;i<maxn;i++)tab1[i]=tab1[i-1]*i%mod;tab2[maxn-1]=mod_reverse(tab1[maxn-1],mod);for(int i=maxn-2;i>=0;i--)tab2[i]=tab2[i+1]*(i+1)%mod;
}
long long C(int a,int b)
{return tab1[a]*tab2[b]%mod*tab2[a-b]%mod;
}int main()
{init();int T;scanf("%d",&T);while(T--){long long n,m,k;scanf("%lld %lld %lld",&n,&m,&k);if(k>(n*m-m))puts("0");else{int t=k/n;long long res=0;for(int i=t;i>=0;i--){long long tmp=n*i;long long left=k-tmp;tmp=((C(m,i)*((i%2)?-1:1))%mod+mod)%mod;tmp=tmp*C(m+left-1,left)%mod;res=(res+tmp)%mod;}printf("%lld\n",res);}}return 0;}

J - Taotao Picks Apples
这题和之前做的题类似，从后往前维护那就是标标准准的单调队列了，既然这样我们可以把询问离线，然后以下标从后往前排序，然后前面的他不用管，后面二分第一个比他大的数就行了。

#include<bits/stdc++.h>
using namespace std;const int maxn=1e5+5;
int h[maxn];
int cnt[maxn],big[maxn];
struct node
{int p,q;int idx;node(int p,int q,int idx):p(p),q(q),idx(idx){}node(){}bool operator<(const node &b)const{return p>b.p;}
}nodes[maxn];
int Q[maxn];
int hh[maxn];
int solve(int num,int r)
{int l=1;int ans=-1;while(l<=r){int mid=l+r>>1;if(h[Q[mid]]>num){ans=mid;l=mid+1;}else r=mid-1;}return ans;
}
int ans[maxn];
int main()
{int T;scanf("%d",&T);while(T--){int n,m;scanf("%d %d",&n,&m);for(int i=1;i<=n;i++){cnt[i]=cnt[i-1];big[i]=big[i-1];scanf("%d",&h[i]);if(h[i]>big[i-1]){cnt[i]++;big[i]=h[i];}}int pp,qq;for(int i=1;i<=m;i++){scanf("%d %d",&pp,&qq);nodes[i]=node(pp,qq,i);}sort(nodes+1,nodes+1+m);int head=0;int now=1;for(int i=n;i>=1;i--){while(nodes[now].p==i){int res=cnt[i-1];int bg=big[i-1];if(nodes[now].q>bg){res++;bg=nodes[now].q;}int idx=solve(bg,head);if(idx!=-1)res+=idx;ans[nodes[now].idx]=res;now++;}while(head>0&&h[i]>=h[Q[head]])head--;Q[++head]=i;}for(int i=1;i<=m;i++)printf("%d\n",ans[i]);}return 0;
}