Semantic Soft segmentation 论文阅读

论文阅读——Semantic Soft segmentation

论文简介

《Semantic Soft segmentation》主要提出了一个用于精确表示软过渡（soft transitions）的方法，通过引入了语义软分割（Semantic Soft Segmentation， 简写为SSS）的概念来精确表示软过渡。SSS是一组对应于图像中有语义意义区域的的layers，其在复杂对象中表现出精确的软过渡 。

? 作者从谱分析的角度处理语义软分割问题。将来自输入图像的纹理和颜色信息与通过使用训练用于场景分析的卷积神经网络生成的高级语义信息相结合。本文设计了一个图结构，在相应的Laplacian矩阵的特征向量中揭示语义对象以及它们之间的软过渡。最后通过引入一个空间变化的层稀疏度模型，该模型可以根据特征向量生成高质量的层，可用于图像编辑。作者演示了使用soft segments可以轻松地完成复杂的图像编辑任务。

问题描述：

给定输入图像，自动生成器软分割结果，即分解为表示场景内物体的不同层，包括物体的透明度和物体间的软过渡。

每一层的每一个像素通过使用透明度$\alpha \in [0,1]$进行增强表示，$\alpha =0$表示完全透明，$\alpha =1$表示完全不透明，中间值则表示不同水平的部分透明度。使用一个附加的图像构成模型进行描述：
$$\begin{gathered} (R,G,B{)}_{input}=\sum _i{\alpha }_i(R,G,B{)}_i \\ \sum _i{\alpha }_i=1 \end{gathered}$$
这样将输入的RGB像素表示为在每个层$i$ 中对应的权重${\alpha }_i$下的和，另外约束$\alpha$在每个像素中的和为1。

本文的方法和spectral matting具有相同形式，都是通过将软分割公式化为一个特征向量评估问题。其中的核心部分是Laplacian矩阵$L$的构建，$L$可以表示图像中每对像素属于同一个分割的可能性。spectral matting仅使用低级的局部色彩分布，本文则使用非局部信息和高级语义信息来增强这个方法。

背景知识

Spectral matting

? 本文的方法建立在 Levin等人的工作上，Levin等人首次提出了matting Laplacian的概念，通过使用局部颜色分布来定义一个矩阵 $L$ ，这个矩阵在一个local batch 上获取每对像素的密切关系，典型的是5×5的batch。根据这个矩阵，在满足用户约束时，最小化二次函数 ${\vec{\alpha }}^{T}L\vec{\alpha }$，其中 $\vec{\alpha }$表示一个层的所有 $\alpha$值。这个数学形式，表明了$L$小特征值对应的向量对高质量mattes有很重要的作用。基于这样的结论，他们后来使用这些向量来建立软分割。每一个软分割是 $L$的$K$ 个最小特征值对应向量的线性组合，并且最大化matting sparsity，例如：最小化部分不透明的出现。分割由最小化一个倾向于$\alpha =0or1$的能量函数确定：
$$\arg \underset{{\vec{y}}_i}{\min }\sum _{i,p}(|{\alpha }_{ip}{|}^{\gamma }+|1?{\alpha }_{ip}{|}^{\gamma }),with{\vec{\alpha }}_i=E{\vec{y}}_i,subjectto:\sum _i{\alpha }_{ip}=1$$
其中 ${\alpha }_{ip}$ 是第 $i$ 个分割的第 $p$ 个像素上的 $\alpha$值， $E$ 是 $K$ 个最小特征向量构成的矩阵，${\vec{y}}_i$是相应的权重向量，$\gamma$ 是一个控制稀疏先验的一个超参数。

? spectral matting在识别对象单一且清晰时可以很好产生满意的结果，但是需要做的是处理多场景和多对象的情况。所以需要在原有基础上添加更加高级的信息。

Affinity and Laplacian matrices

Levin等人将问题形式化一个最小二乘优化问题，并直接引向一个Laplacian矩阵。一个替代的方法是表述每一对像素之间的关系(Affinity) [Aksoy et al.2017a]. 具有正近似相关的像素对有更大的可能有相同的 $\alpha$值，0近似相关的像素对是独立的，负近似关系的像素对应该有不同的值。本文采用的是关系这一方法，据此对应一个标准化的Laplacian矩阵：
$$L=D^{?\frac{1}{2}}(D?W)D^{?\frac{1}{2}}$$
其中 $W$是包含所有像素对近似关系的方阵，D则是一个度矩阵（是对角矩阵）。

非局部颜色关系(Nonlocal Color Affinity)

? 为了表示较大范围的像素对之间的关系，作者定义了一个附加的低级关系项(low-level affinity term)。作者提出了基于图像的过度分割（over-segmentation）的引导采样（guided sampling），使用SLIC[Achanta et al.2012] 生成2500个超像素，然后评估超像素之间的近似关系 (Affinity)，并且满足在一个半径内的所有超像素对应于图像小小的20%。这种方法的优点是每个特征都足够大而成为超像素，但稀疏性仍然很高，以为使用的是每个超像素的单个样本，并且可以使用较大的半径连接可能断开的区域。最后，对于两个由小于20%的图像尺寸的距离分割的超像素 $s$ 和 $t$ ，定义它们的质心的颜色关系（color affinity）$w_{s,t}^C$：
$$w_{s,t}^C=(erf(a_c(b_c?\parallel c_s?c_t\parallel ))+1)/2$$
其中 $c_s,c_t\in [0,1]$ 是超像素的均值颜色, erf 是高斯误差函数，$a_c,b_c$ 是控制affinity下降的速率和变为0的阈值。

本文使用的参数值为: $a_c=50,b_c=0.05$.

这种关系本质上保证了颜色非常相似的区域在复杂场景结构中的连接性，其效果如下图：

高级语义关系（High-Level Semantic Affinity）

? 虽然非局部颜色关系在分割过程添加了较大范围的相互作用，但它仍然是一个低级特征。实验表明，在没有附加信息的情况下，分割仍然经常合并属于不同对象的颜色相似的图像区域。为了创建受语义相似区域限制的片段，我们添加了一个语义关系——鼓励对属于同一场景对象的像素进行分组，并且阻止来自不同对象的像素进行分组。我们基于对象识别领域中的先前工作，计算与底层对象相关的每个像素的特征向量。通过使用神经网络计算相应的特征，生成的特征向量应该使得：如果两个像素点 $p$ 和 $q$ 属于的相同的对象 $f_p$ 和 $f_q$, 那么有 $\parallel f_p?f_q\parallel \equiv 0$，并且对不同分割区域的第三个像素 $r$ ，$ f_r$应该远远不同：$\parallel f_p-f_q\parallel\ll \parallel f_p-f_r\parallel$

? 对于每个超像素 $s$，我们将它的均值特征向量 ${\tilde{f}}_s$与质心联系起来。于是我们可以这个特征向量来定义两个超像素$s,t$之间的关系：
$$w_{s,t}^S=erf\left(a_s(b_s?\parallel {\tilde{f}}_s?{\tilde{f}}_t\parallel )\right)$$
添加之后的效果如下：

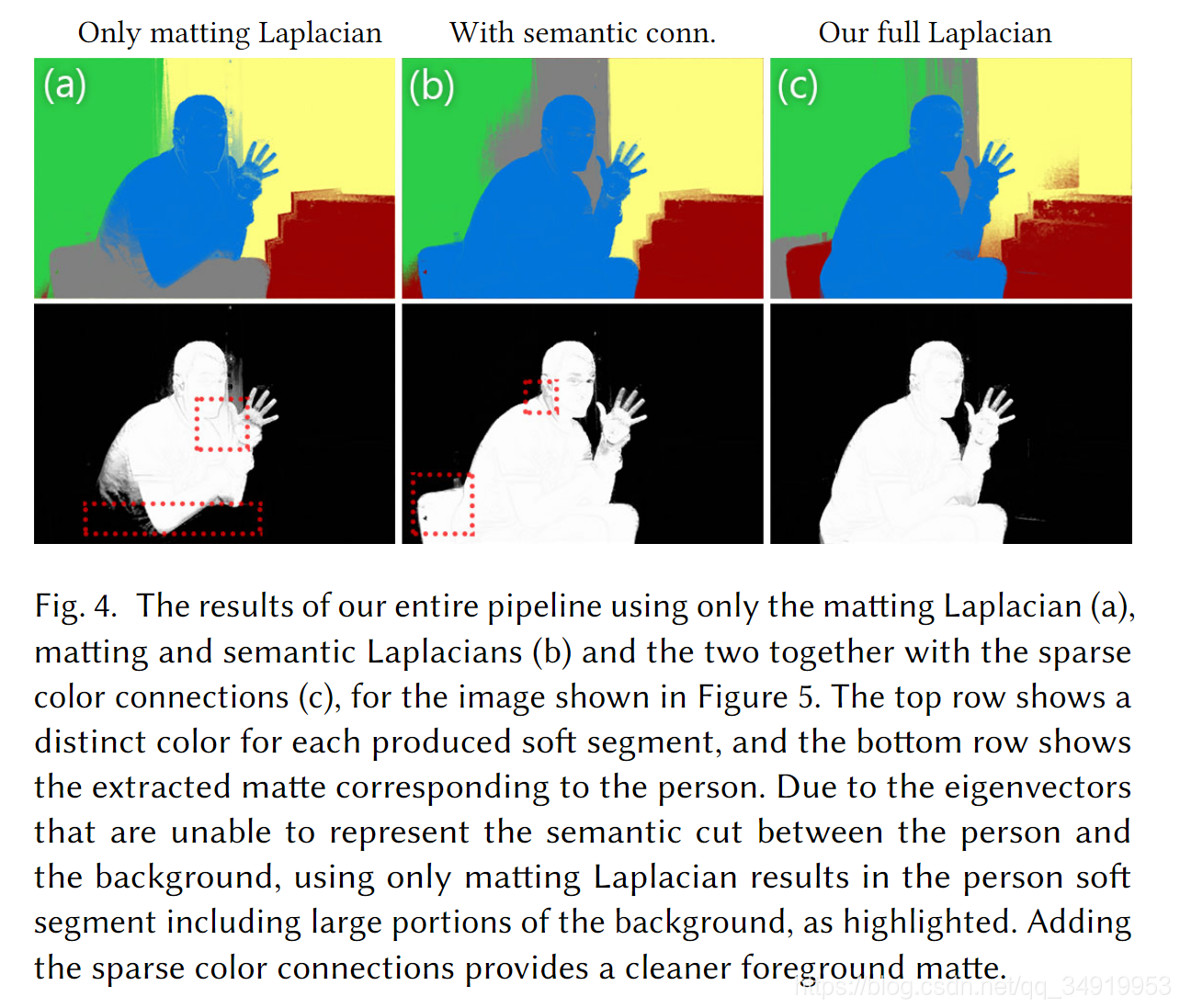
图像层的建立(Creating the Layers)

Laplacian矩阵的形成(Forming the Laplacian matrix)

构建Laplacian矩阵通过之前添加的关系矩阵，有：
$$L=D^{?\frac{1}{2}}(D?(W_L+{\sigma }_S{W}_S{\sigma }_C{W}_C))D^{?\frac{1}{2}}$$
其中 $W_L$是包含matting关系的矩阵，$W_C$ 是包含非局部颜色关系的矩阵，$W_S$ 是包含语义关系的矩阵，${\sigma }_S,{\sigma }_C$ 是控制相应矩阵影响力的参数，全部设置为0.01

稀疏化约束(Constrained sparsification)

提取 $L$ 矩阵的100个最小特征值对应的特征向量，在下式的优化过程中令 $\gamma =0.8$
$$\arg \underset{{\vec{y}}_i}{\min }\sum _{i,p}(|{\alpha }_{ip}{|}^{\gamma }+|1?{\alpha }_{ip}{|}^{\gamma }),with{\vec{\alpha }}_i=E{\vec{y}}_i,subjectto:\sum _i{\alpha }_{ip}=1$$
与直接在特征向量上使用k-means聚类来初始化spectral matting不同，本文在由特征向量 $f$ 表示的像素使用k-means聚类。这样的初始化与场景的语义更加一致，并且可以产生更好的软分割。在实际中，用这个方法来生成40层，再去除不重要的15-25层。再使用 $k=5$ 的k-means算法来进一步减少由平均特征向量表示的不重要层。这种方法比直接将100个特征向量稀疏化为5层更好，因为这种急剧减少会使问题过度约束并且不会产生好的结果，特别是在mattte sparsity方面。另外，不失一般性，可以将分割数设置为5。虽然这个数字可以用用户根据场景设置，但是根据观察，这对大多数图像来说都是合理的。因为这5个层被约束在有限数量的特征向量的子空间内，所以事先的稀疏性是次优的，在层中留下许多的半透明区域，而这在普通场景中是不可能的。
约束对比见下图：

放宽稀疏化(Relaxed sparsification)

为了改善层的稀疏性，选择放宽他们特征向量的线性组合的约束。并不通过调整系数 $y_i?$ 来处理，而是通过调节 $\alpha$。
首先，放宽子空间约束，并且仅确保生成的层保持靠近使用稀疏化约束过程中创建的层 $\hat{\alpha }$：
$$E_F=\sum _{ip}({\alpha }_{ip}?{\hat{\alpha }}_{ip}{)}^2$$
同时放宽累加为1的要求，作为软约束集成到线性系统中：
$$E_C=\sum _p{\left(1?\sum _i{\alpha }_{ip}\right)}^2$$
其中，${\alpha }_{ip}$ 表示在第 $i$ 层上第 $p$ 个像素的 $\alpha$ 值。下面是Laplacian $L$定义的能量，它定义了 $L=D^{?\frac{1}{2}}(D?(W_L+{\sigma }_S{W}_S{\sigma }_C{W}_C))D^{?\frac{1}{2}}$ 的空间传播：
$$E_L=\sum _i{\vec{\alpha }}_i^{T}L{\vec{\alpha }}_i$$
最后，我们制定了一个适应图像内容的稀疏性术语。直观地，部分像素来自图像中的颜色过渡，因为在许多情况下，它对应于两个场景元素之间的过渡，例如，泰迪熊和背景之间的模糊过渡。 我们使用这种观察来建立一个空间变化的稀疏能量：
$$E_S=\sum _{i,p}|{\alpha }_{ip}{|}^{{\tilde{\gamma }}_p}+|1?{\alpha }_{ip}{|}^{{\tilde{\gamma }}_p}with{\tilde{\gamma }}_p=\min (0.9+\parallel ?c_p\parallel ,1)$$
将这些项放在一起，可以得到：
$$E=E_L+E_S+E_F+\lambda E_C$$

语义特征向量(Semantic Feature Vectors)

在高层特征构建时，相同物体的像素的特征向量相似，不同物体的像素的特征向量不同.
特征向量是采用语义分割的深度网络模型训练和生成的.

这里采用了 DeepLab-ResNet-101 作为特征提取器，但网络训练是采用的是度量学习方法，最大化不同物体的特征间的 L2 距离(稍微修改了 N-Pair loss)

在 COCO-Stuff 数据集上进行语义分割网络的训练. 采用 guided filter 将网络生成的 feature map 与图像进行边缘对齐. 然后采用 PCA 降低 feature map 维度到 3. 最后，归一化特征向量值到 [0, 1].