复习策略梯度policy gradient
计算在某一个state,采取action a的概率。到游戏结束为止,获得多少reward。
G很不稳定。除非sample很多。

复习Q-learning
用期望代替sample,value-based
第一种方法算V,用π和环境做互动,看到s之后,累计reward期望值是多少。
第二种方法,用π,当再s采取a,累计reward是多少。
TD比较稳,MC比较精确。
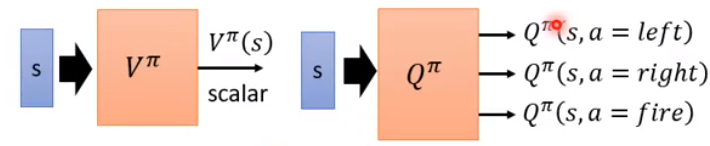
Actor-Critic
算G的期望,即是Q,即在s采取a的累计reward期望值。
V与action无关,Q与action有关。

这样要预测两个网络Q和V。
所以用r+V代替Q。
因为s采取a变成的st+1是什么不确定,所以用期望。但是比较麻烦,去掉期望。r是一个变量,但是比G的方差比较小。

π和环境互动,学习Value function。套用下面的式子学到新的π。

Tip:
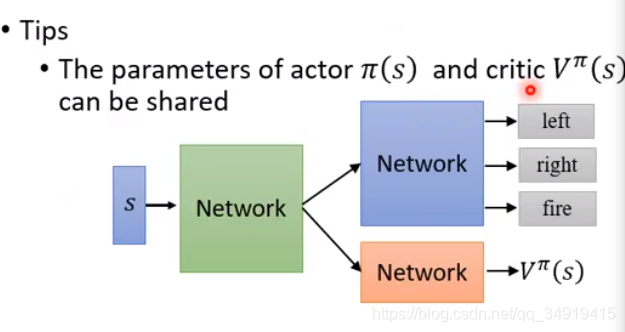
1.π和V的参数可以被分享。
2.不同的action采取的几率平均一点,这样可以尝试探索。
比如把网络设计成这样。让前面几层公用同一个参数。
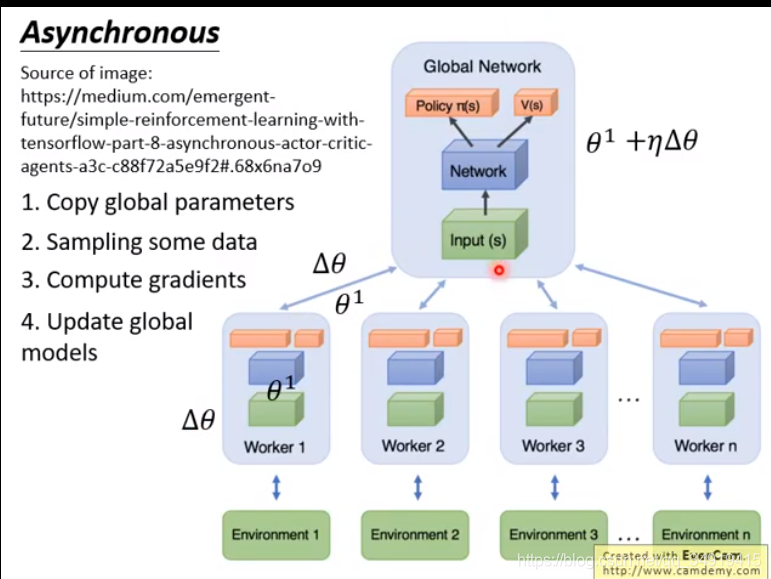
A3C 为了加快训练
开很多worker,每个worker和环境做互动。
复制全局参数,sample一些data,计算梯度,更新全局模型。
所有的actor是平行的,互不相关。就是复制参数跑。有可能等跑完了全局参数已经变了,但是没关系。
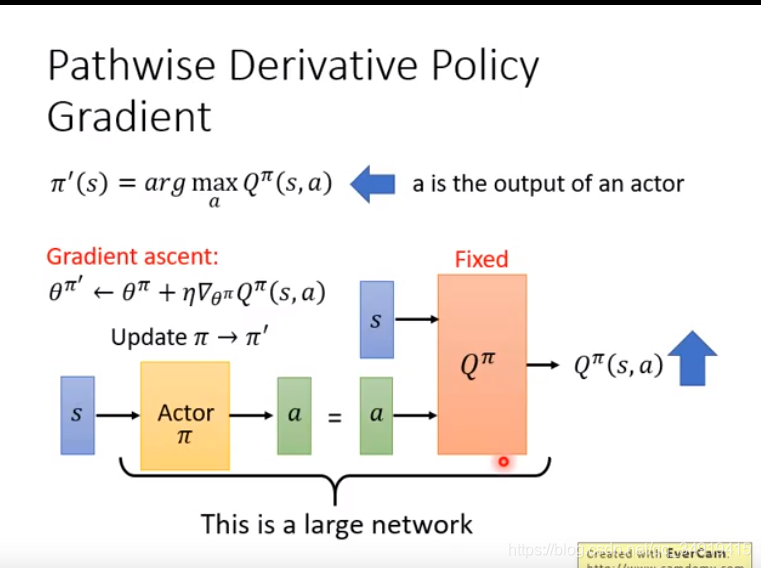
Pathwise Derivative Policy Gradient
输入s,输出a,让Q越大越好。固定Q参数,只调整Actor的参数
就是一个gan。Q就是辨别器,A是生成器。
用π生成a。有一个target π,平常是固定的。
