update on 2019/4/1
我计划在今年六月份开源我的人脸识别demo到github上，集成了人脸检测和mobileFaceNet + arcloss人脸识别。如果需要请下方留言。届时会通知各位。
updata on 2019/4/20
因为一些原因，我提前开源了我的人脸识别代码，请见github地址。如果觉得对你的工作有帮助，请有账号的帮忙点个star哦。你的一个star是对我开源贡献的肯定。
前情提要
ceter loss提出了可视化在某种损失函数下样本的分布，在此基础上sphere face，norm face，cos face的出现，都揭示了一个现象，最后一个全连接层的权重W的每一列，都代表了每一类的样本中心向量（放后面解释）
作者认为他们提出的损失函数有四点优势
- Engaging（有吸引力?）:arcFaca 直接优化能测量出的距离（角度距离），这种优化是通过规范化的超球体的确切的联系实现的。
- Effective：因为state of the art ，而且在10个人脸识别benchmarks上测试效果都很好。
- Easy：容易实现
- Efficient：仅仅需要少量的多余计算
正文
首先回忆一下softmax loss
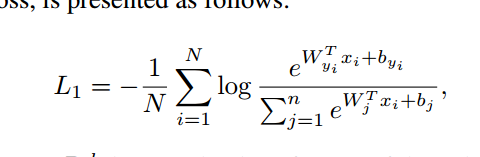
这里先说下变量的含义。
是一个batch的第i个样本对应的embedding vector，就是在最后的全连接层前面那层输出的结果，是一个d维向量。
是最后一层全连接层的权重的第yi行，w是一个（d，n）的矩阵，n是分类的数目，d是向量维度。那么w的转置就是(d,n)的。
yi是xi的标签。比如说xi的标签是98，那么n是从0开始的，肯定要大于或者等于98。
就是w的第99列。
那么，
是一个在shape 是(n,N)的矩阵中的第j行，第i列的元素。
在center loss那篇论文中，提到了softmax在人脸识别领域的短板，通过可视化发现，softmax损失函数在embedding 空间的分布是沿原点发散的。也就是类与类之间的区别依据在于他们之间的角度。这也就是为啥softmax loss不能减小类内距离。
那么现在我们看一下
的变形：
就是向量内积的结果是向量各自的模相乘，在乘上向量夹角的cos值。作者由NormFace得到的启发，将权重w和embedding vector归一化，这样保证了模值为1。那么向量相乘得到的结果其实就是xi对应在第j类的夹角。ArcFace就是从这个角度上做文章。
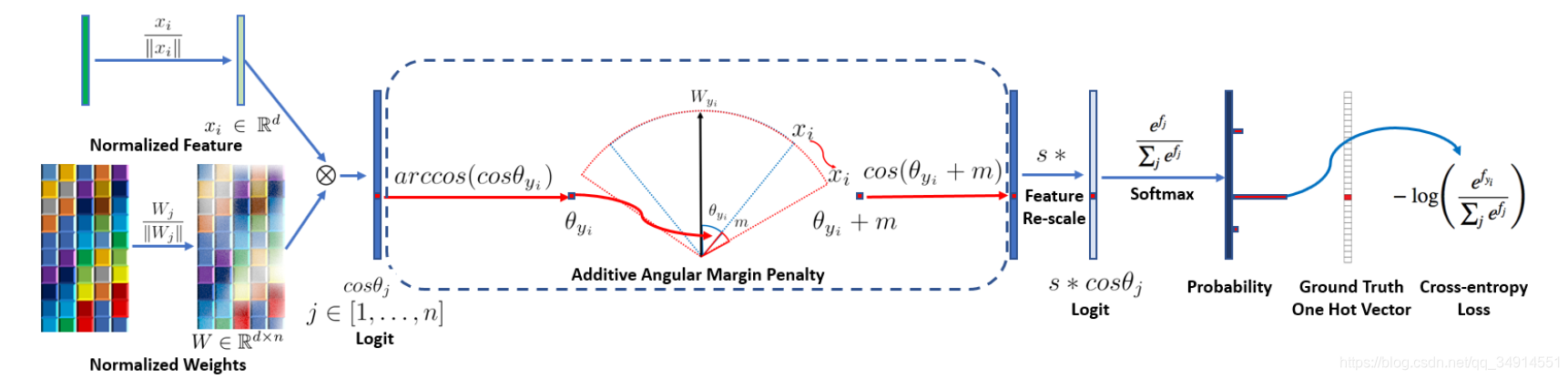
从左至右，我们看看大致顺序，后面会分析这一部分的源码。
先对权重和向量都归一化，这样得到的乘积就是xi和Wj之间夹角的余弦值。然后通过arccos求出角度。这个角度加上一个指定的值m，论文指出0.5是最佳值。这里的角度都是弧度制。然后在求出cos值，乘上一个scale，再送入softmax，之后都和我们熟知的交叉熵是一样的。
回顾一下，我们就可以发现，既然用w的列向量和xi的角度表示类之间的夹角，那么我们可以知道网络在更新w的时候，逐渐把w的每列变成这一类的中心向量。所以我们才能用x和w的列向量夹角描述类别的相近程度。
重新再看一次这个过程。首先W.T*X是一个(n,N）的矩阵，n是类别数目，N是batch size。经过归一化得到的结果就是余弦值，所以在这个矩阵中，第i行第j列的意义就是batch中第j个样本在特征空间的向量和第i类的中心向量的夹角。这个角度越小，则xj属于第i类的置信度越大。
Arcloss在角度空间加入了margin，使得类别的分隔在特征维度从原点发散的更加开了，也就加强了类别的区分度。
实验对比
作者展示了三种阶段：训练开始阶段，中间阶段和末尾阶段，三个时段的样本和类中心的夹角分布。
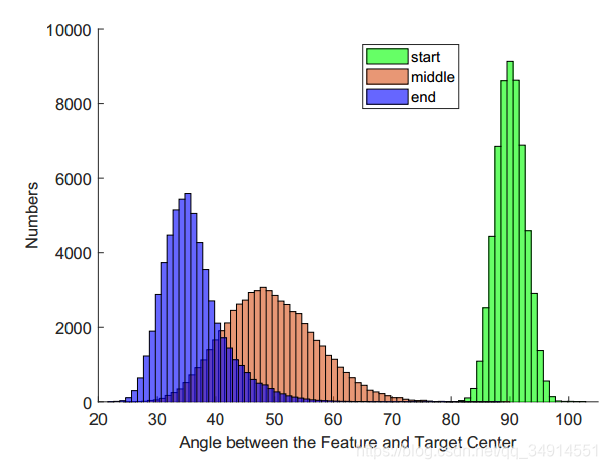
在训练结束时，样本和类中心向量的夹角可以被控制在25-55之间。
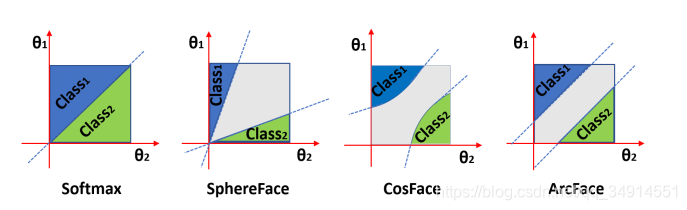
这里是一个几何解释，为什么arcface效果这么好。cosface在余弦空间加入margin，放射会角度空间，就会有第三张图的那种曲线；而arcface之间在角度空间加入了margin，那么超平面就像svm留下了margin。
文中作者还在很多benchmark上做了对比实验，可以说工作量是很大了。有两个方面：损失函数的比较：用不同的损失函数在几个数据集上测试，第二个方面是使用不同的模型作为backbone。这些都是很容易看懂的内容。面试也基本不会问这些不是核心的内容，就不多介绍了。