EMANet：Expectation-Maximization Attention Networks for Semantic Segmentation论文解读和代码解读

官方项目地址：含论文和代码

来自北大才子 立夏之光的 ICCV Oral ，理论很漂亮。属于Non local方式

Updated on 2020.1.6
最近一直有人私信我，这个attention map怎么初始化，我厌其烦，就在博客里面补上获得attention map的代码，作者源码里面是没有可视化attention map的代码。

idea

由于理论方面涉及了机器学习算法 - EM算法，博主虽然学过EM，但时间久远有些记不起，这篇论文吧博主看了很久，依然没能理解其精髓，但是不影响我会使用它（哈哈）。言归正传。

在语义分割中，越来越多Non local的方法出现了，并且都取得了精度上的进步，说明Non local确实是有用的。但是这些方法都不能避免庞大的计算量，比如DANet，有很大的矩阵相乘。

EMANet的提出正是为解决Non local带来的计算量过于庞大。通过EM，E步学习一组attention maps， M步更新一组基，经过几次迭代之后，用基和maps 重构特征。 基的向量长度可以是个比较小的数值，我们可以理解为通过把原始特征降维，在低维的流形中建模像素之间的联系，这样的话，可以省略很多计算量。然后通过基和attention maps 重构出高维的、带有全局性的信息的特征。用这个特征在去做最后的分割。

network

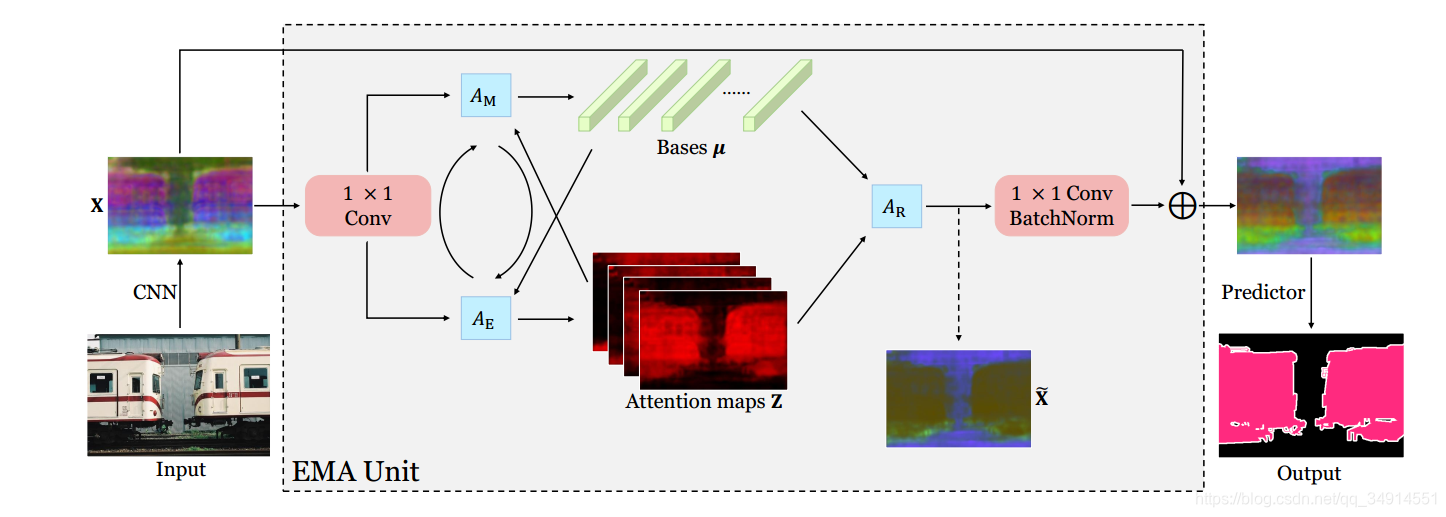
本文不关注理论，只关注步骤，因为理论是在太难弄懂了。有关理论，可以去看第一作者的知乎专栏。

• 经过一个CNN-based backjbone 得到特征X，经过一个 1x1的卷积降维，（因为ResNet最后的卷积输出的是2048通道的，太大了），降至512个通道。假设$X\in R^{N\times C},N=H\times W$。 H和W是特征图X的分辨率尺寸。
• 初始化一个$\mu \in R^{K\times C}$作为基， K指的是有K个基。
• E步： 得到attention maps， 记作Z。 $Z=softmax(\lambda X{\mu }^T)\in R^{N\times K}$， 即有K个maps， 每一个map的尺寸是H x W （N)
• M步： 更新基$\mu$，得到的maps Z， 先在第2个维度，即（dim=1，从0开始算）求和，做一个normlize。具体看代码解读部分。
• 在每次M步之后，为了保证$\mu$的学习是稳定的，选择L2Norm对$\mu$做归一化。
• E步和M步重复T次，T在论文中为3。
• 训练中使用moving average更新$\mu$，测试阶段跳过这一步。
• 用得到的maps Z和基$\mu$重构X，得到$\tilde{X}\in R^{N\times C}$
• 然后把$\tilde{X}$reshape到CxHxW。送到接下来的segHead中。

基不是公共的。每一个样本经过迭代都会得到各自的基，因为不同图像的分布不一样。

Attention Maps

那么既然一组低维空间的基和一组maps（都是K个），能够学习到Non local的信息，那么我们自然该看看这些maps长得是什么样子吧。

我在网上找了一张图像，里面的类别都是VOC数据集出现的。
一共有64个maps，下面是一部分。

从上图中，可以发现模型确实在低维流形中学习到了Non loca的信息，还减小了计算量。而且通过降维学习（低秩）学习的基可以说是没有冗余的（正交基）。

code explain

下面的代码块是EMA（EM attention） 模块的代码。

    def forward(self, x):idn = x# The first 1x1 convx = self.conv1(x)# The EM Attentionb, c, h, w = x.size()x = x.view(b, c, h*w)               # b * c * nmu = self.mu.repeat(b, 1, 1)        # b * c * k # k 个 基with torch.no_grad():for i in range(self.stage_num):  # 迭代T次x_t = x.permute(0, 2, 1)    # b * n * cz = torch.bmm(x_t, mu)      # b * n * kz = F.softmax(z, dim=2)     # b * n * kz_ = z / (1e-6 + z.sum(dim=1, keepdim=True)) # 这一步对应论文 sec4.2，reweight X的公式mu = torch.bmm(x, z_)       # b * c * kmu = self._l2norm(mu, dim=1)  # 为了让基的学习更稳定，并且不改变基的方向，保持基的正交性。（正交是冗余最低的形式）z_t = z.permute(0, 2, 1)            # b * k * nx = mu.matmul(z_t)                  # b * c * nx = x.view(b, c, h, w)              # b * c * h * wx = F.relu(x, inplace=True)# 跳跃链接x = self.conv2(x)x = x + idnx = F.relu(x, inplace=True)return x, mu

整个模型的forward结构如下

 def forward(self, img, lbl=None, size=None):x = self.extractor(img)    # backbonex = self.fc0(x)            # 降维到512个通道x, mu = self.emau(x)       # 经过EMA模块x = self.fc1(x)            # seg Headx = self.fc2(x)if size is None:size = img.size()[-2:]pred = F.interpolate(x, size=size, mode='bilinear', align_corners=True) # 向原图大小插值。这里不能用label向特征大小差值，因为label在原图空间填充了ignore label，如果对label下采样，会破坏ignore label的值。if self.training and lbl is not None:loss = self.crit(pred, lbl)return loss, muelse:return pred

还有一个地方值得注意，在EMA模块里，

mu = torch.Tensor(1, c, k) # 512 64
mu.normal_(0, math.sqrt(2. / k)) # Init with Kaiming Norm.
mu = self._l2norm(mu, dim=1)
self.register_buffer(‘mu’, mu)

$\mu$的初始化这样的。$\mu$不是一个Parameter，而是一个buffer。对应原文，基的训练方式，究竟是通过反向传播训练还是moving average。

attention map可视化

首先要知道，众多的变量中，哪个是attention map。

	...b, c, h, w = x.size()x = x.view(b, c, h*w)               # b * c * nmu = self.mu.repeat(b, 1, 1)        # b * c * k # k个基with torch.no_grad():for i in range(self.stage_num):x_t = x.permute(0, 2, 1)    # b * n * cz = torch.bmm(x_t, mu)      # b * n * kz = F.softmax(z, dim=2)     # b * n * kz_ = z / (1e-6 + z.sum(dim=1, keepdim=True)) # 这一步是为啥？论文 sec4.2mu = torch.bmm(x, z_)       # b * c * kmu = self._l2norm(mu, dim=1)z_t = z.permute(0, 2, 1)            # b * k * nself.z = z_t.view(b, mu.size(2), h, w)  # b * k * h * w...

倒数第二行的z就是attention map，当然这个时候z的shape不是我们要的，所以先换轴，在reshape。
在EMANet的forward中，加入

   self.attention_maps = F.interpolate(self.emau.z, size=size,mode='bilinear', align_corners=True)

把attention map resize至原图大小。
然后在Session 的call中，获取attention map

    def __call__(self,img):img = self.preprocessing(img)with torch.no_grad():logit = self.net(img)pred = logit.max(dim=1)[1]attention_map = self.net.module.attention_maps  # 这里得到attention mapreturn pred.data.squeeze(0).cpu().numpy(), attention_map.data.squeeze(0).cpu().numpy()

在main函数中，保存即可，但是在保存之前别忘了将数值范围normalize到0-255，还的是opencv支持的uint8型。

  pred, attention_maps = sess(image[:,:,::-1].copy())# print(pred.shape)# print(attention_maps.shape)if not os.path.exists('./attentionMaps'):os.makedirs('./attentionMaps')for i in range(attention_maps.shape[0]):attention_map = attention_maps[i]attention_map = (attention_map - attention_map.min()) / (attention_map.max() - attention_map.min())attention_map = attention_map *255cv2.imwrite('./attentionMaps/' + str(i)+ '.jpg', np.uint8(attention_map))

所以不要再问我attention map如何可视化了，我也不会再回答了。