噪声：Practical Poissonian-Gaussian noise modeling and fitting for single-image raw-data_综合

Practical Poissonian-Gaussian noise modeling and fitting for single-image raw-data

文章目录

Practical Poissonian-Gaussian noise modeling and fitting for single-image raw-data
- Poissonian-Gaussian Modeling
- The Noise Profile Algorithm
- - Wavelet domain analysis
  - Segmentation
  - Local estimation of expectation/standard-deviation pairs
- Clipping

Sensor的噪声特性是确定一款特定Sensor是否满足最终产品规格需求的重要指标，这篇文章是Alessandro Foi于2007年发表的论文《 Noise Measurement for Raw-Data of Digital Imaging Sensors by Automatic Segmentation of Nonuniform Targets》的基础上所提出的用于Sensor噪声分析的框架，其噪声模型也是目前市场上常见的芯片噪声分析(Noise Proflie)模块的基础模型，Alessandro Foi是芬兰Tampere大学研究图像去噪和噪声建模的教授，他的文章谈到的方法很多都已经在手机camera中得到了应用。不同于Imatest所使用到的基于傅里叶变换的方法 ISO 15739 — Noise measurements，本文所提的方法基于简单的图像分割，简单易行。
随着Sensor制成工艺的日益进步，Sensor的像素尺寸越来越小，其所能够积累的光子数量越来越少，最终造成Sensor采集下来信号(Raw)信噪比的下降，同时Sensor的噪声也并不是一般图像处理过程中所假设的高斯白噪声，因此对Sensor所采集图像信号的噪声的正确建模对于后续的图像处理过程是十分重要的。

Poissonian-Gaussian Modeling

参考《CMOS图像传感器中的噪声来源分析》一文中对CMOS Sensor的噪声来源的分析，我们知道Sensor采集下来的Raw数据当中最主要的噪声是泊松噪声和高斯噪声，且这两部分噪声都是白噪声，将这两部分噪声的观测模型做如下表示：
$z(x)=y(x)+σ(y(x))ξ(x)(1)z(x)=y(x)+\sigma(y(x)) \xi(x)\tag{1}$
其中 $x∈Xx\in X$ 表示像素坐标， $z$ 为当前点被噪声影响后的观测像素值， $y$ 为当前点不被噪声影响的实际像素值， $ξ(x)\xi(x)$ 表示均值为0，标准差为1的随机变量， $σ\sigma$ 为 $y$ 的函数，表示噪声的标准差随实际像素值变化， $σ(y(x))ξ(x)\sigma(y(x)) \xi(x)$ 表示Raw数据的噪声是均值为0、方差随实际像素值变化的而变化随机变量，即可以将Sensor的噪声模型看做是一个异方差的高斯噪声( Heteroskedastic Normal)。在接下来的描述当中将使用 $E?{?}\operatorname{E}\{\cdot\}$ 表示随机变量的数学期望， $var?{?}、std?{?}\operatorname{var}\{\cdot\}、\operatorname{std}\{\cdot\}$ 分别表示随机变量的方差与标准差。由于 $E{ξ(x)}=0E\{\xi(x)\}=0$ ，就有 $E\{z(x)\}=y(x)$ ，原始信号可以被看做是噪声信号的期望，而噪声信号的方差与观察信号、原始信号间的关系如下：
$std{z(x)}=σ{y(x)}=σ(E{z(x)})(2)std\{z(x)\}=\sigma\{y(x)\}=\sigma(E\{z(x)\})\tag{2}$
Sensor当中的泊松噪声来源于其散粒噪声及暗电流，高斯噪声来源于热噪声、复位噪声、量化噪声，可以将这两类噪声看做是相互独立的两部分，分别用 $ηp、ηg\eta_{p}、\eta_{g}$ 表示如下：
$σ(y(x))ξ(x)=ηp(y(x))+ηg(x)(3)\sigma(y(x)) \xi(x)=\eta_{\mathrm{p}}(y(x))+\eta_{\mathrm{g}}(x)\tag{3}$

$χ(y(x)+ηp(y(x)))?P(χy(x)),ηg(x)?N(0,b)(4)\chi\left(y(x)+\eta_{\mathrm{p}}(y(x))\right) \sim \mathcal{P}(\chi y(x)), \quad \eta_{\mathrm{g}}(x) \sim \mathcal{N}(0, b)\tag{4}$

其中 $P\mathcal{P}$ 表示泊松分布， $N\mathcal{N}$ 表示高斯分布， $χ＞0、b≥0\chi＞0、b≥0$ 分别为尺度参数。由于泊松分布的方差与均值相等，即有：
$E{χ(y(x)+ηp(y(x)))}=var?{χ(y(x)+ηp(y(x)))}=χy(x)(5)E\left\{\chi\left(y(x)+\eta_{\mathrm{p}}(y(x))\right)\right\}=\operatorname{var}\left\{\chi\left(y(x)+\eta_{\mathrm{p}}(y(x))\right)\right\}=\chi y(x)\tag{5}$
又由于 $var?{χ(y(x)+ηp(y(x)))}=χ2var{ηp(y(x))}=χy(x)\operatorname{var}\left\{\chi\left(y(x)+\eta_{\mathrm{p}}(y(x))\right)\right\}=\chi ^{2}var\{\eta_{p}(y(x))\}=\chi y(x)$ ，即有 $var?{ηp(y(x))}=y(x)/χ\operatorname{var}\left\{\eta_{\mathrm{p}}(y(x))\right\}=y(x) / \chi$ 且 $E{ηp(y(x))}=0E\left\{\eta_{\mathrm{p}}(y(x))\right\}=0$ ，因此泊松噪声的方差随 $y (x)$ 而变化，记为：
$var?{ηp(y(x))}=ay(x);a=χ?1(6)\operatorname{var}\left\{\eta_{\mathrm{p}}(y(x))\right\}=a y(x);a=\chi^{-1}\tag{6}$
因此式(1)中的噪声部分可以做如下表示：
$σ2(y(x))=ay(x)+b(7)\sigma^{2}(y(x))=a y(x)+b\tag{7}$
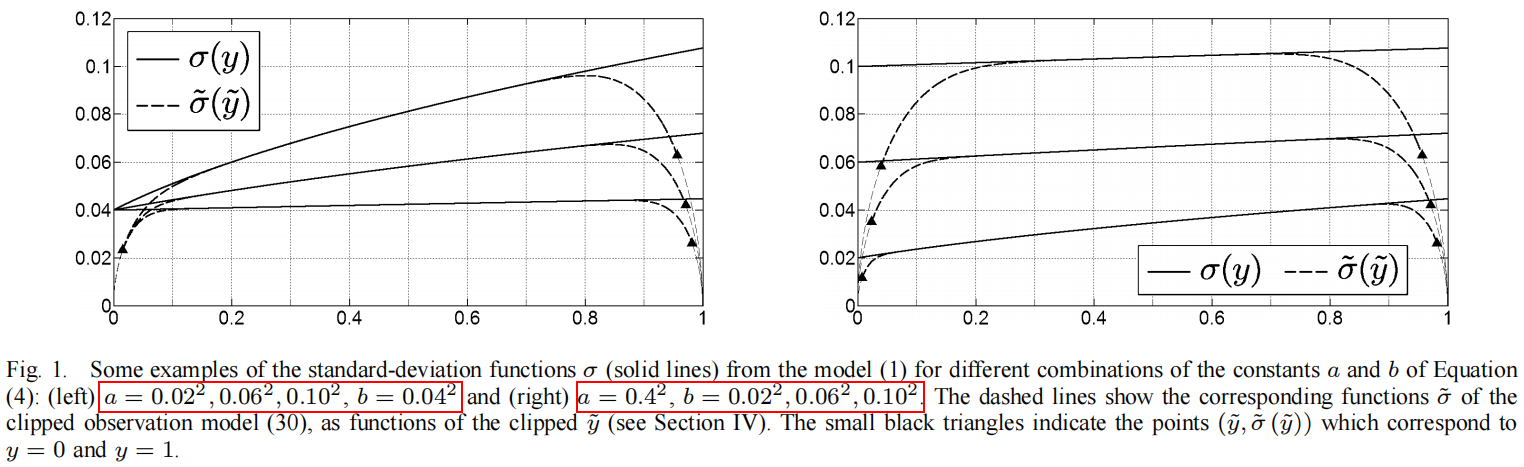
噪声：Practical Poissonian-Gaussian noise modeling and fitting for single-image raw-data

作：原图；右：添加a=0.01、b=0.0016泊松-高斯噪声后的观测图

噪声：Practical Poissonian-Gaussian noise modeling and fitting for single-image raw-data
上图为向原图 $y$ 中所添加噪声的噪声参数 $α、b\alpha、b$ 取不同值时，最后通过本文方法标定出来的信号期望与噪声方差间的关系示意图，其中实线为添加噪声时所假设的噪声模型，对应的虚线是本文方法对该噪声的标定结果，在首尾两端出现的不一致是由于收尾两端的像素值受噪声干扰后很容易出现小于0或者大于255的情况，最后分别被Clip至0或255造成的(在图像处理中一般需要做Clip的原因是，希望被处理图像数据的灰度值范围固定在8bit、10bit、12bit的范围内，以节省计算、存储等资源)。
为了更进一步的简化噪声模型，用高斯分布来进一步近似泊松分布，即：
$P(λ)≈N(λ,λ)\mathcal{P}(\lambda) \approx \mathcal{N}(\lambda, \lambda)$
当 $λ\lambda$ 足够大时，可以将泊松分布看做是异方差的高斯分布，此时泊松-高斯分布的噪声模型可以进一步简化为：
$σ(y(x))ξ(x)=ay(x)+bξ(x)?ηh(y(x))(8)\sigma(y(x)) \xi(x)=\sqrt{a y(x)+b} \xi(x) \simeq \eta_{\mathrm{h}}(y(x))\tag{8}$
其中 $ηh(x)?N(0,ay(x)+b)\eta_{\mathrm{h}}(x) \sim \mathcal{N}(0, a y(x)+b)$ 。

The Noise Profile Algorithm

Wavelet domain analysis

通常情况下，我们并不能直接获取 $(σ,y)(\sigma,y)$ 的数据对来拟合式(8)所示噪声模型的参数 $α,b\alpha,b$ ，用小波分解的方式将图像分解为低频部分 $z^{wapp}$ 、高频部分 $z^{wdet}$ ，其中低频部分包含了大部分的原始信号，高频部分包含了大部分的噪声信号，文章中选择局部特性较好的DB3小波作为小波基函数，分解过程如下：
$=↓2(z?φ)z^{\text {wdet }}=\downarrow_{2}(z \circledast \psi)\\ z^{\text {wapp }}=\downarrow_{2}(z \circledast \varphi)$
其中：
$ψ=ψ1?ψ1Tφ=φ1?φ1T\psi=\psi_{1} \circledast\psi_{1}^{T}\\ \varphi=\varphi_{1} \circledast \varphi_{1}^{T}$
$ψ1=[0.0350.085?0.135?0.4600.807?0.333]φ1=[0.025?0.060?0.0950.3250.5710.235].\begin{aligned} &\psi_{1}=\left[\begin{array}{llllll} 0.035 & 0.085 & -0.135 & -0.460 & 0.807 & -0.333 \end{array}\right] \\ &\varphi_{1}=\left[\begin{array}{llllll} 0.025 & -0.060 & -0.095 & 0.325 & 0.571 & 0.235 \end{array}\right] . \end{aligned}$
如上，做小波分解的目的是做如下近似：
$})(9)\begin{aligned} \operatorname{std}\left\{z^{\text {wdet }}\right\} &=\downarrow_{2}(\operatorname{std}\{z \circledast \psi\})=\downarrow_{2}\left(\sqrt{\operatorname{var}\{z\} \circledast \psi^{2}}\right) \\ & \simeq \downarrow_{2}\left(\operatorname{std}\{z\}\|\psi\|_{2}\right)=\downarrow_{2}(\operatorname{std}\{z\})\\ &=\downarrow_{2}(\sigma(y))=\sigma\left(\downarrow_{2} y\right)=\sigma\left(\downarrow_{2}\left(y \sum \varphi\right)\right) \\ & \simeq \sigma\left(\downarrow_{2}(y \circledast \varphi)\right)=\sigma\left(E\left\{z^{\text {wapp }}\right\}\right) \end{aligned}\tag{9}$

Segmentation

在上面计算出来的高频信息 $z^{wdet}$ 中还包含了大量了边缘信息，为了避免边缘信息对噪声分析过程的干扰，检测边缘并将边缘区域排在统计数据之外。首先对 $z^{wapp}$ 再次进行低通滤波，再次滤波其中的高频成分：
$∥?∥1=1(10)z^{\mathrm{smo}}=z^{\mathrm{wapp}} \circledast \varpi;\varpi \geq 0 \text { and }\|\varpi\|_{1}=1\tag{10}$
如果原始信号 $y$ 处于平坦区域，那么可以认为 $zsmo≈E{zwapp}≈↓2yz^{smo}≈E\{z^{wapp}\}≈\downarrow_{2} y$ 。然后用平滑后的 $z^{wdet}$ 近似图像的局部标准差：
$s=π2∣zwdet∣??(11)s=\sqrt{\frac{\pi}{2}}\left|z^{\mathrm{wdet}}\right| \circledast \varpi\tag{11}$
通过比较 $z^{app}$ 的梯度与以上的图像的局部标准差来判断图像中出处于平坦区域的点集：
$)(11)X^{\mathrm{smo}}=\left\{x \in \downarrow_{2} X:\right. \left.:\left|\nabla\left(\Lambda\left(z^{\text {wapp }}\right)\right)(x)\right|+\left|\Lambda\left(z^{\text {wapp }}\right)(x)\right|<\tau \cdot s(x)\right\}\\ \Lambda\left(z^{\text {wapp }}\right)=\nabla^{2} \text { medfilt }\left(z^{\text {wapp }}\right)\tag{11}$
其中 $?、?2\nabla、\nabla^{2}$ 分别为梯度算法和拉普拉斯算子，medfilt为 $3 \times 3$ 的中值滤波， $τ>0\tau>0$ ，总的来说是通过叠加梯度算子和拉普拉斯算子并与局部标准差进行比较来获取边缘信息，去除图像的边缘区域，保留平滑区域，相当于以是否平滑为依据对图像做二值化。最后再将平滑区域的像素点，根据其像素值划分为若干个不重合的区域：
$Si={x∈Xsmo:zsmo(x)∈[ui?Δi/2,ui+Δi/2)}(12)S_{i}=\left\{x \in X^{\mathrm{smo}}: z^{\mathrm{smo}}(x) \in\left[u_{i}-\Delta_{i} / 2, u_{i}+\Delta_{i} / 2\right)\right\}\tag{12}$
噪声：Practical Poissonian-Gaussian noise modeling and fitting for single-image raw-data

Local estimation of expectation/standard-deviation pairs

根据上面分割出来的区域，分区域计算对原始信号、噪声方差的估计：
$y^i=1ni∑j=1nizwapp (xj),{xj}j=1ni=Siσ^i=1κni∑j=1ni(zwdet(xj)?zˉiwdet)2ni?1(13)\hat{y}_{i}=\frac{1}{n_{i}} \sum_{j=1}^{n_{i}} z^{\text {wapp }}\left(x_{j}\right), \quad\left\{x_{j}\right\}_{j=1}^{n_{i}}=S_{i}\\ \hat{\sigma}_{i}=\frac{1}{\kappa_{n_{i}}} \sqrt{\frac{\sum_{j=1}^{n_{i}}\left(z^{\mathrm{wdet}}\left(x_{j}\right)-\bar{z}_{i}^{\mathrm{wdet}}\right)^{2}}{n_{i}-1}}\tag{13}$
其中：
$(xj)κn=2n?1Γ(n2)Γ(n?12)=1?14n?732n2+O(1n3)(14)\bar{z}_{i}^{\text {wdet }}=\frac{1}{n_{i}} \sum_{j=1}^{n_{i}} z^{\text {wdet }}\left(x_{j}\right)\\ \kappa_{n}=\sqrt{\frac{2}{n-1}} \frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n-1}{2}\right)}=1-\frac{1}{4 n}-\frac{7}{32 n^{2}}+O\left(\frac{1}{n^{3}}\right)\tag{14}$
$κn\kappa_{n}$ 服从自由度为 $n ? 1$ 的卡方分布。根据大数定理，当且仅当 $n→∞n\to \infty$ 时， $y^→y、σ^→σ\hat{y}\to y、\hat{\sigma} \to \sigma$ ，再根据中心极限定理，大量相互独立的随机变量的和的分布以正态分布为极限：
$var?{y^i}=σ2(yi)ci;var?{σ^i}=σ2(yi)dici=∥φ∥22ni;di=1?κni2κni2=12ni+58ni2+O(1ni3)(15)\operatorname{var}\left\{\hat{y}_{i}\right\}=\sigma^{2}\left(y_{i}\right) c_{i};\operatorname{var}\left\{\hat{\sigma}_{i}\right\}=\sigma^{2}\left(y_{i}\right) d_{i}\\ c_{i}=\frac{\|\varphi\|_{2}^{2}}{n_{i}};d_{i}=\frac{1-\kappa_{n_{i}}^{2}}{\kappa_{n_{i}}^{2}}=\frac{1}{2 n_{i}}+\frac{5}{8 n_{i}^{2}}+O\left(\frac{1}{n_{i}^{3}}\right)\tag{15}$
即：
$y^i?N(yi,σ2(yi)ci);σ^i?N(σ(yi),σ2(yi)di)(16)\hat{y}_{i} \sim \mathcal{N}\left(y_{i}, \sigma^{2}\left(y_{i}\right) c_{i}\right);\hat{\sigma}_{i} \sim \mathcal{N}\left(\sigma\left(y_{i}\right), \sigma^{2}\left(y_{i}\right) d_{i}\right)\tag{16}$
最后再根据估算出来的期望-方差对拟合最终的噪声模型，选用最常用的最小二乘法即可：
$σ2(y)=ay+b\sigma^{2}(y)=a y+b$
以上即是本文所提出的噪声分析算法，结果如下图：
噪声：Practical Poissonian-Gaussian noise modeling and fitting for single-image raw-data

Clipping

这篇文章的一个突出贡献是分析了由噪声带来的Clipping对噪声模型的影响，首先，我们将Sensor采集下来的Raw数据的动态范围normalize到[0,1]之间，将Clipping做如下定义：
$z~(x)=max?(0,min?(z(x),1))(17)\tilde{z}(x)=\max (0, \min (z(x), 1))\tag{17}$
其中 $z$ 为含噪信号，则Clipping过后的含噪信号的期望为：
$y~(x)=E{z~(x)}(18)\tilde{y}(x)=E\{\tilde{z}(x)\}\tag{18}$
将此时的噪声模型表示为：
$z~(x)=y~(x)+σ~(y~(x))ξ~(x)(19)\tilde{z}(x)=\tilde{y}(x)+\tilde{\sigma}(\tilde{y}(x)) \tilde{\xi}(x)\tag{19}$
与以上噪声模型相同 $E{ξ~(x)}=0,var?{ξ~(x)}=1E\{\tilde{\xi}(x)\}=0, \operatorname{var}\{\tilde{\xi}(x)\}=1$ ，并且 $σ~(y~(x))=std?{z~(x)}\tilde{\sigma}(\tilde{y}(x))=\operatorname{std}\{\tilde{z}(x)\}$ ，但是需要特别注意的是Clipping后果的数据与没有Clipping的数据间存在如下差异：
$y~(x)=E{z~(x)}≠E{z(x)}=y(x)(y~(x))=std?{z~(x)}≠std?{z(x)}=σ(y(x))(20)\tilde{y}(x)=E\{\tilde{z}(x)\} \neq E\{z(x)\}=y(x)\\ (\tilde{y}(x))=\operatorname{std}\{\tilde{z}(x)\} \neq \operatorname{std}\{z(x)\}=\sigma(y(x))\tag{20}$
特别需要注意的是，即使 $var?{ξ~(x)}=var?{ξ(x)}=1\operatorname{var}\{\tilde{\xi}(x)\}=\operatorname{var}\{\xi(x)\}=1$ ， $ξ~(x)\tilde{\xi}(x)$ 与 $ξ(x)\xi(x)$ 也并不是同一分布。再回顾上面给出过的Fig 1中的虚线部分，这一部分与原分布曲线出现较大差异的原因就是Clipping造成的，由此也可以清晰地知道，Clipping影响最为严重的是原信号接近0或1处，由此，我们得出一个经验性的总结：

①当原始信号 $y→0y\to0$ ，由于噪声服从异方差的正态分布，则 $z < 0$ 的概率远大于 $z > 1$ ，此时发生的Clipping为 $z~=max(0,z)\tilde{z}=max(0,z)$

②当原始信号 $y→1y\to1$ ，由于噪声服从异方差的正态分布，则 $z > 1$ 的概率远大于 $z < 0$ ，此时发生的Clipping为 $z~=min(z,1)\tilde{z}=min(z,1)$

③当原始信号 $0 < < y < < 1$ 时，可以认为发生Clipping的概率很小，但并不为0

针对①、②两种Clipping情况，先侧重分析Clipping至0的情况，首先，由于 $z~=max(0,z)\tilde{z}=max(0,z)$ ，则此时观测数据的期望为：
$E{z~}≥E{z}=y(21)E\{\tilde{z}\} \geq E\{z\}=y\tag{21}$
将含噪信号看做如下随机变量 $ν?N(μ,1)\nu \sim \mathcal{N}(\mu, 1)$ ，其观测值 $v~=max(v,0)\tilde{v}=max(v,0)$ ，则此时 $v~\tilde{v}$ 的概率密度函数为：
$fν~(t)={?(t?μ)+Φ(?μ)δ0(t)t≥00t<0(22)f_{\tilde{\nu}}(t)= \begin{cases}\phi(t-\mu)+\Phi(-\mu) \delta_{0}(t) & t \geq 0 \\ 0 & t<0\end{cases}\tag{22}$
其中 $δ0\delta_{0}$ 为狄拉克函数， $?\phi$ 为 $N(0,1)\mathcal{N}(0,1)$ 的概率密度函数， $Φ\Phi$ 为 $N(0,1)\mathcal{N}(0,1)$ 累积分布函数， $fν~(t)f_{\tilde{\nu}}(t)$ 的具体表现形式如下：
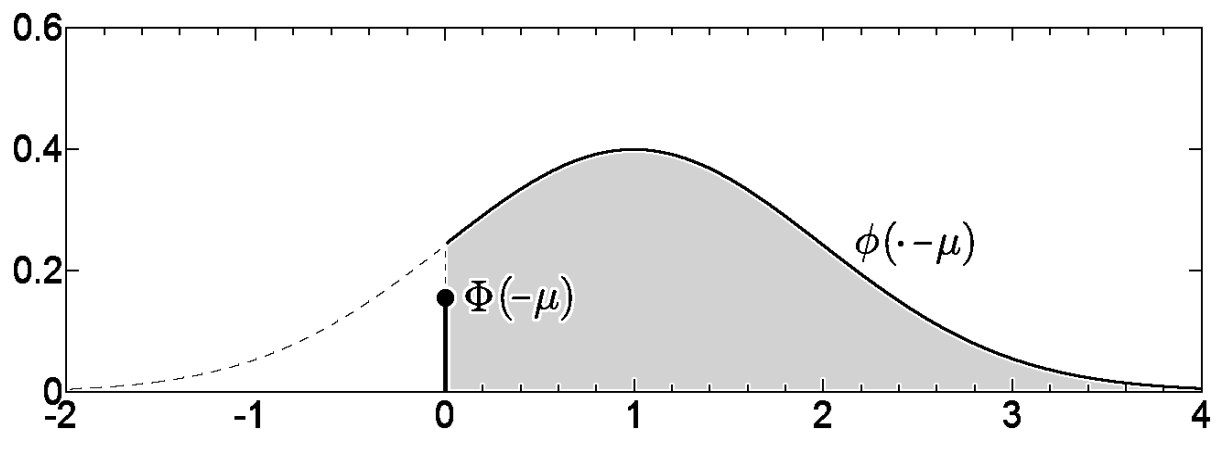
噪声：Practical Poissonian-Gaussian noise modeling and fitting for single-image raw-data
此时计算观测值 $v~\tilde{v}$ 的期望与方差如下：
$E{ν~}=Φ(μ)μ+?(μ)var?{ν~}=Φ(μ)+?(μ)μ??2(μ)++Φ(μ)μ(μ?Φ(μ)μ?2?(μ))(23)\begin{aligned} E\{\tilde{\nu}\} &=\Phi(\mu) \mu+\phi(\mu) \\ \operatorname{var}\{\tilde{\nu}\} &=\Phi(\mu)+\phi(\mu) \mu-\phi^{2}(\mu)++\Phi(\mu) \mu(\mu-\Phi(\mu) \mu-2 \phi(\mu)) \end{aligned}\tag{23}$
其中 $μ=E{ν}\mu=E\{\nu\}$ ，此时观测数据 $v~\tilde{v}$ 的期望与 $E\{v\}$ 间的关系表示为 $Em\mathcal{E}_{m}$ ，观测数据 $v~\tilde{v}$ 的方差与 $E\{v\}$ 间的关系表示为 $Sm\mathcal{S}_{m}$ ，如下图：
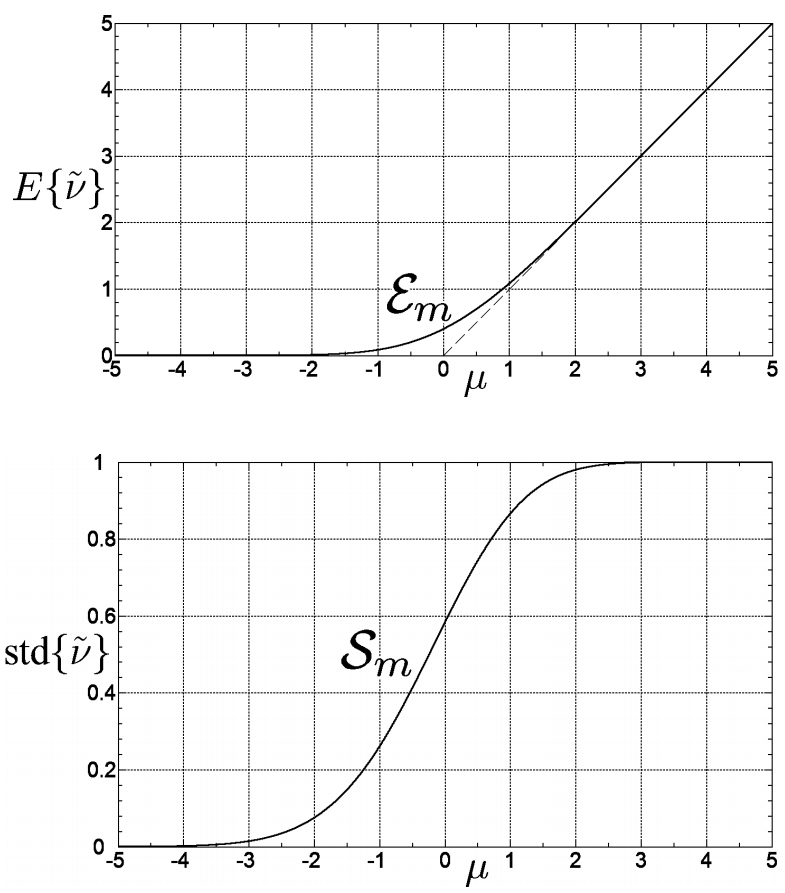
噪声：Practical Poissonian-Gaussian noise modeling and fitting for single-image raw-data

即是 $μ\mu$ 为负数， $E{v~}E\{\tilde{v}\}$ 依旧为正，当 $μ→?∞\mu \rightarrow-\infty$ 时， $E{v~}→0，std{v~}→0E\{\tilde{v}\} \to0，std\{\tilde{v}\}\to0$ ；当 $μ→+∞\mu \rightarrow+\infty$ 时， $E{v~}→μ，std{v~}→1E\{\tilde{v}\} \to \mu，std\{\tilde{v}\}\to1$ ，很容易扩展为由异方差噪声造成的Clipping与原始信号间的关为：
$y~(x)=E{z~(x)}=σ(y)E{ν~}std?{z~}=σ(y)std?{ν~}(24)\tilde{y}(x)=E\{\tilde{z}(x)\}=\sigma(y) E\{\tilde{\nu}\}\\ \operatorname{std}\{\tilde{z}\}=\sigma(y) \operatorname{std}\{\tilde{\nu}\}\tag{24}$
可以简单地将服从异方差正态分布的随机变量 $\sim \mathcal{N}\left(y, \sigma^{2}(y)\right)$ 重新标准化为一个方差为1的随机变量 $zσ(y)?N(yσ(y),1)\frac{z}{\sigma(y)} \sim \mathcal{N}\left(\frac{y}{\sigma(y)}, 1\right)$ ，由此，可以将 $y~、σ~\tilde{y}、\tilde{\sigma}$ 与 $y、σy、\sigma$ 联系起来：
$y~=σ(y)Em(yσ(y))σ~(y~)=σ(y)Sm(yσ(y))(25)\begin{aligned} \tilde{y} &=\sigma(y) \mathcal{E}_{m}\left(\frac{y}{\sigma(y)}\right)\\ \tilde{\sigma}(\tilde{y}) &=\sigma(y) \mathcal{S}_{m}\left(\frac{y}{\sigma(y)}\right) \end{aligned}\tag{25}$
如果用 $Se\mathcal{S}_{e}$ 来表示上图中 $Em、Sm\mathcal{E}_{m}、\mathcal{S}_{m}$ 间的关系，如下图：
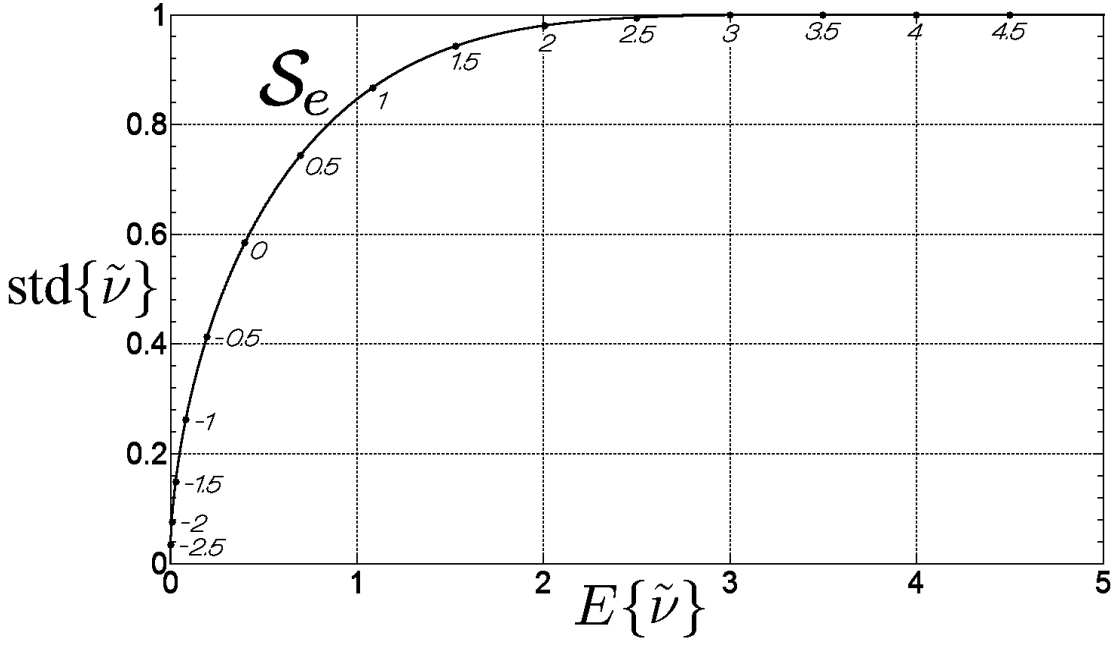
噪声：Practical Poissonian-Gaussian noise modeling and fitting for single-image raw-data
则可将 $y~、σ~\tilde{y}、\tilde{\sigma}$ 联系起来：
$σ~(y~)=σ(y)Se(y~σ(y))(26)\tilde{\sigma}(\tilde{y})=\sigma(y) \mathcal{S}_{e}\left(\frac{\tilde{y}}{\sigma(y)}\right)\tag{26}$
接下来分析Clipping至1的情况，由正态分布的对称性，可以将Clipping至1的情形做如下等价：
$y?1?y,z?1?zy~?1?y~,z~?1?z~\begin{array}{l} y\quad\longleftrightarrow \quad 1-y, \quad z \longleftrightarrow 1-z\\ \tilde y\quad\longleftrightarrow \quad 1-\tilde y, \quad \tilde z \longleftrightarrow 1-\tilde z\\ \end{array}$
即有：
$y~=1?σ(y)Em(1?yσ(y))σ~(y~)=σ(y)Sm(1?yσ(y))=σ(y)Se(1?y~σ(y))\begin{aligned} \tilde{y} &=1-\sigma(y) \mathcal{E}_{m}\left(\frac{1-y}{\sigma(y)}\right) \\ \tilde{\sigma}(\tilde{y}) &=\sigma(y) \mathcal{S}_{m}\left(\frac{1-y}{\sigma(y)}\right)=\sigma(y) \mathcal{S}_{e}\left(\frac{1-\tilde{y}}{\sigma(y)}\right) \end{aligned}$
由此可以从Clipping的数据的分布中恢复出原噪声分布，其恢复结果如下：
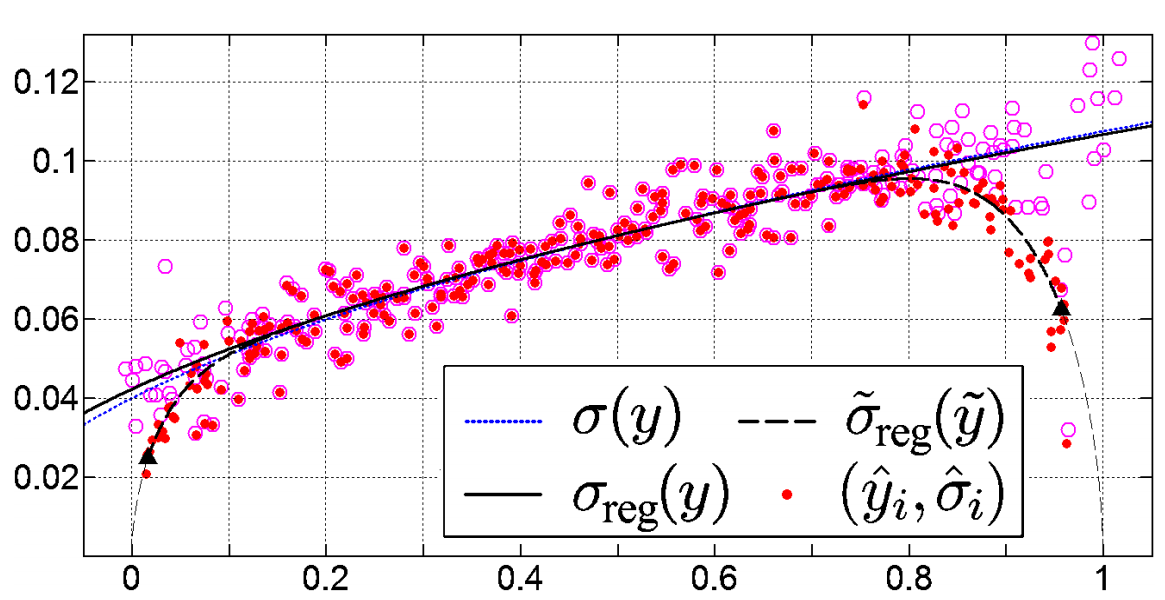
噪声：Practical Poissonian-Gaussian noise modeling and fitting for single-image raw-data
本文提及的对Clipping数据的校正方法虽然应用在对噪声分布的校正当中，此方法也是将Clipping数据复原的方法，可以直接用于Clipping数据的复原当中。