定义
- 最短路径:在一幅加权有向图中,从顶点s到顶点v的最短路径指的是所有s到t中路径权重的最小者。
- 最短路径树:包含起点s到所有可达顶点的最短路径,s为根节点,树中的每条路径都是一条最短路径。
最短路径的性质
- 路径是定向的。 最短的路径必须遵循其边缘的方向。 权重不一定是距离。 几何直觉可能会有所帮助,但是边缘权重权重可能代表时间或成本。
- 并非所有顶点都需要可达。 如果t不能从s到达,则根本没有路径,因此从s到t没有最短的路径。 负权重会带来并发症。
- 假设边缘权重为正(或为零)。 最短路径通常很简单。 我们的算法忽略了形成循环的零权重边缘,因此它们找到的最短路径没有循环。
- 最短路径不一定是唯一的。 从一个顶点到另一个顶点可能有多个权重最低的路径;我们满足于找到其中任何一个。 可能存在平行边缘和自环。
- 假设不存在平行边,并使用符号v-> w来指代从v到w的边,但是我们的代码可以轻松地处理它们。
摘自《算法 第四版》
最短路径API

数据结构:
- 父亲数组
edgeTo[],edgeTo[v]为s到v的最短路径上的最后一条边。 - 距离数组
distTo[v],s到v的最短路径的长度 - 约定:设起点为
s,初始化edgeTo[s]为null,dsitTo[s]为0,其他元素的值初始化为不可达【起点s不可达的距离设为浮点数最大值DBL_MAX】。
边的松弛
- 什么是松弛?
两颗钉子间拉着一条橡皮筋,紧绷绷的。现在,找一个更近的钉子,当把橡皮筋一端换到这里时,缓解了橡皮筋的压力。
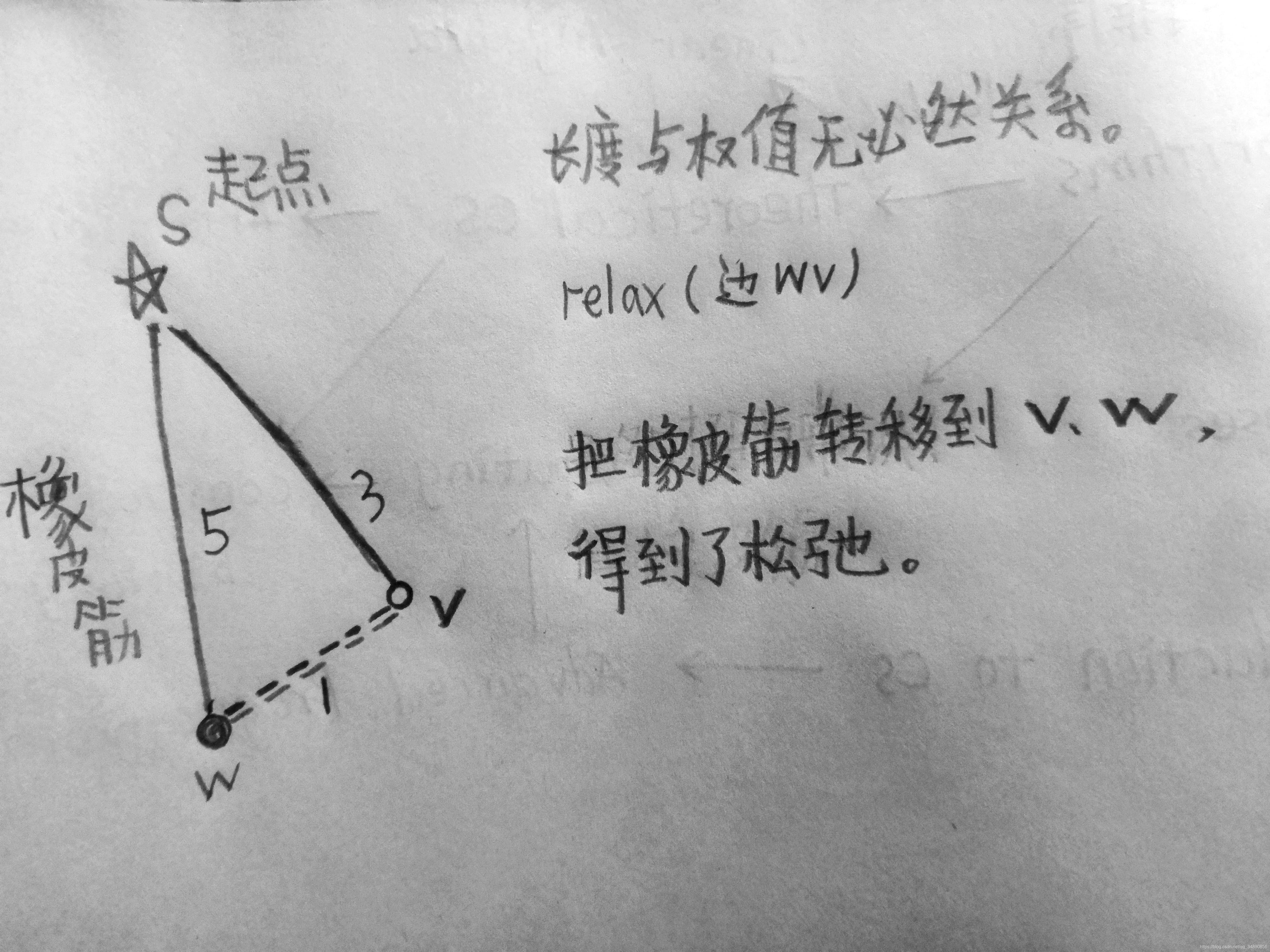
- 代码描述
void relax(DirectedEdge &e){
int v=e.from(),w=e.to();if(distTo[w]>distTo[v]+e.weight()){
distTo[w]=distTo[v]+e.weight();//换到更近的钉子上,橡皮筋成功松弛edgeTo[w]=e;}
}
- 图示说明
左边松弛失败,右边松弛成功
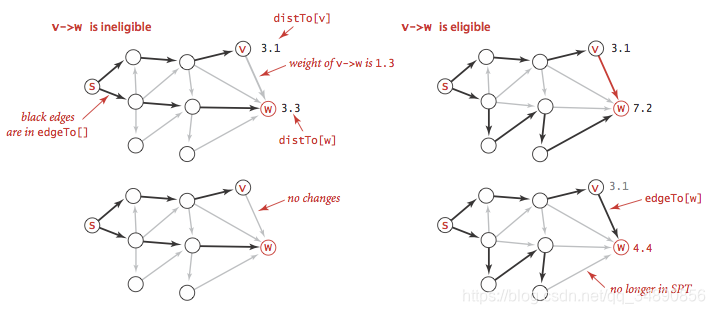
顶点的松弛
放松从一个给定顶点指出的所有边。
注意,从任意distTo[v]【起点s到v的距离】为有限值的顶点v到distTo[]为无穷的顶点的边都是有效的。如果v被放松,那么这些有效边都会被加到edgeTo[]。显然某条从起点指出的边将会是第一条被加入到edgeTo[]中的边。
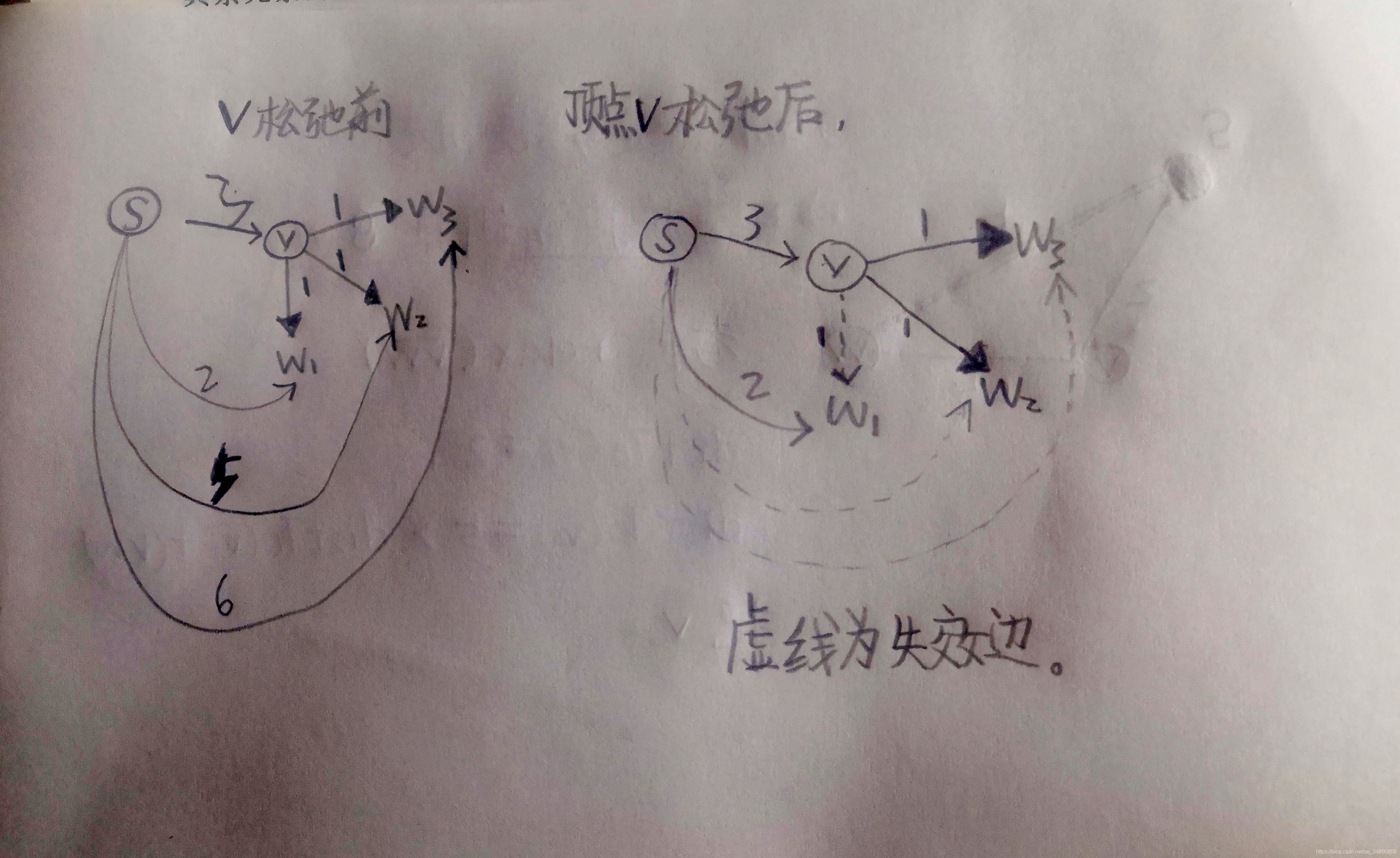
代码描述:
void relax(EdgeWeightedDigraph G,int v){
for(DirectedEdge e: G.adj(v)){
//检查v的所有邻接点int w=e.to();if(distTo[w]>distTo[v]+e.weight()){
distTo[w]=distTo[v]+e.weight();edgeTo[w]=e;//起点指向w最短路径的最后一条边}}
}
命题P(最短路径的最优性条件)
令G是一幅加权有向图,顶点s是G中的起点,distTo[]是一个由顶点索引的数组,保存的是G中的路径长度。
对于从s可达的所有顶点v,distTo[v]的值是s到v的某条路径的长度,对于从s不可达的所有顶点v,该值为无穷大。
当且仅当对于v到w的任意一条边e,这些值都满足distTo[w] <= distTo[v]+e.weight()时(换句话说,不存在有效边时),他们是最短路径长度。
关于证明:

通用的最短路径算法
将distTo[s]初始化为0,其他distTo[]初始化为无穷大,继续如下操作
放松G中的任意边,直到不存在有效边为止。
对于任意从s到w的顶点,distTo[w]的值就是起点s到w的最短路径的长度,且edgeTo[w]为该路径上的最后一条边。