一、LSTM神经网络
1、关于传统RNN网络梯度消失的问题
https://blog.csdn.net/dchen1993/article/details/53885490
http://www.cnetnews.com.cn/2017/1118/3100705.shtml
其中涉及到softmax函数的求导:https://blog.csdn.net/u014313009/article/details/51045303
传统RNN网络梯度消失主要是因为,在往回求导时,St和St-1...S1,S0都有联系,因此都需要对它们求导,所以:
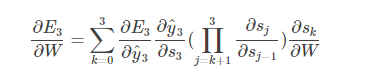



如果我们使用标准化初始w,那么各个层次的相乘都是0-1之间的小数,而激活函数f的导数也是0-1之间的数,其连乘后,结果会变的很小,导致梯度消失。若我们初始化的w是很大的数,w大到乘以激活函数的导数都大于1,那么连乘后,可能会导致求导的结果很大,形成梯度爆炸。 https://www.cnblogs.com/pinking/p/9418280.html
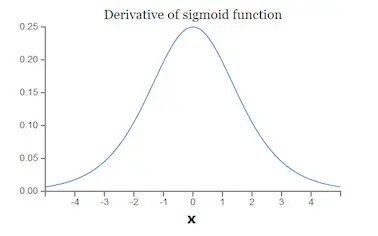

梯度消失和梯度爆炸本质上是一样的,都是因为网络层数太深而引发的梯度反向传播中的连乘效应。
RNN中的损失函数 :
https://www.cnblogs.com/wuxiangli/p/7096392.html
https://www.cnblogs.com/puheng/p/9379730.html
2、RNN中梯度消失的解决方案
①ReLU激活函数+合适的参数初始化 ②LSTM或GRU ③梯度裁剪(Clipping Gradient)
①ReLU激活函数+合适的参数初始化
换成ReLU在一定程度上可以解决梯度消失的问题,但是:
那为什么同样的方法在RNN中不奏效呢?其实这一点Hinton在它的IRNN论文里面(arxiv:[1504.00941] A Simple Way to Initialize Recurrent Networks of Rectified Linear Units)是很明确的提到的:
也就是说在RNN中直接把激活函数换成ReLU会导致非常大的输出值。
一方面,将tanh换成ReLU,最后前向传播时计算的结果会变成多个W连乘:
假设采用ReLU替代传统RNN中的激活函数,并且假设ReLU函数一直处于激活区域(即输入大于0),
则有: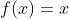 ;
; 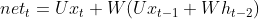 .
.
将其继续展开,![]() 中最终将包含t个W连成。如果W不是单位举证,则
中最终将包含t个W连成。如果W不是单位举证,则![]() 的结果最终将趋于0或者无穷大,引发严重的数值问题。
的结果最终将趋于0或者无穷大,引发严重的数值问题。
同时,假设采用ReLU激活函数,且一开始所有的神经元都处于激活状态,在梯度传递了n层之后,有: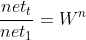
可以看到,只要W不是单位矩阵,梯度还是会出现消失或者爆炸的问题。
综上所述,当采用ReLU作为激活函数时,只有当W的取值在单位矩阵附近的时候,才能取得比较好的效果。
②LSTM或GRU
LSTM或GRU通过门控机制使梯度的乘法变成了加法。
https://www.cnblogs.com/wuxiangli/p/7096392.html
③梯度裁剪
既然在BP过程中会产生梯度消失(就是偏导无限接近0,导致长时记忆无法更新),那么最简单粗暴的方法,设定阈值,当梯度小于阈值时,更新的梯度为阈值,如下图所示: 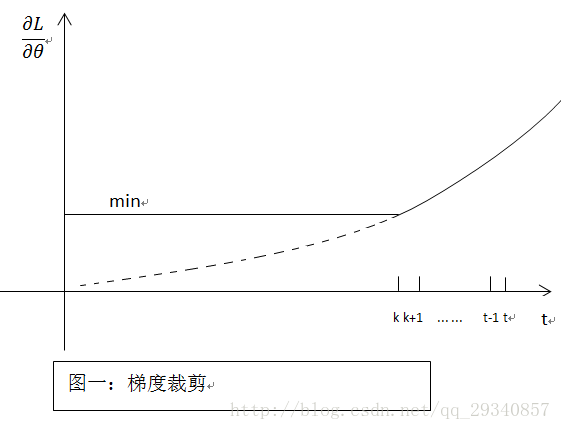
优点:简单粗暴
缺点:很难找到满意的阈值
以上的梯度裁剪的方法一般是用来解决梯度爆炸问题的,用于解决梯度消失的问题还有待查阅。。。
3、LSTM神经网络为什么可以解决传统RNN网络梯度消失的问题
LSTM或GRU通过门控机制使梯度反向传播时由乘法变成了加法。
https://zhuanlan.zhihu.com/p/28749444 这里写的很好!
https://www.cnblogs.com/wuxiangli/p/7096392.html 这篇文章对RNN中的很多问题都进行了详细的介绍。值得一看
4、LSTM神经网络和GRU联系和区别
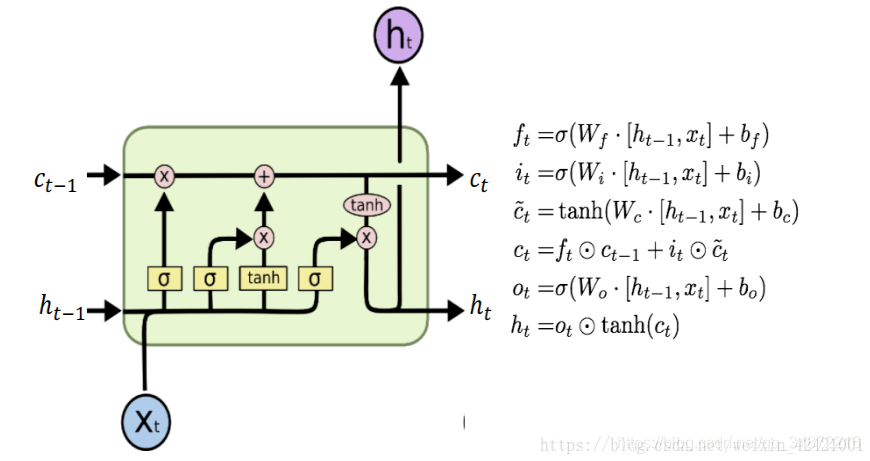
遗忘门:
作用对象:上一个时间步的记忆单元Ct-1
作用:将上一个时间步的记忆单元中的信息选择性的遗忘
输入门:
作用对象:当前计算得到的新状态
作用:将新的信息选择性的记录到细胞状态中
输出门:
作用对象:当前的记忆单元Ct
输出门用来控制当前的记忆单元Ct 有多少被过滤掉。
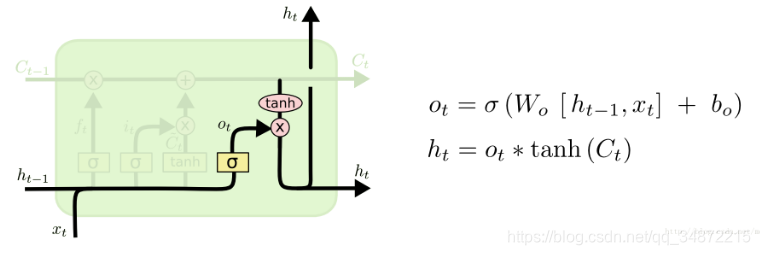
GRU不像LSTM的三门控,它虽然也有门,但是只有两个,分别叫做重置门(reset gate),和更新门(update gate)。重置门顾名思义,控制着是否重置,也就是说多大程度上擦除以前的状态state;更新门则表示,多大程度上要用candidate 来更新当前的hidden layer。下面是另一种示意图,以及它的公式:
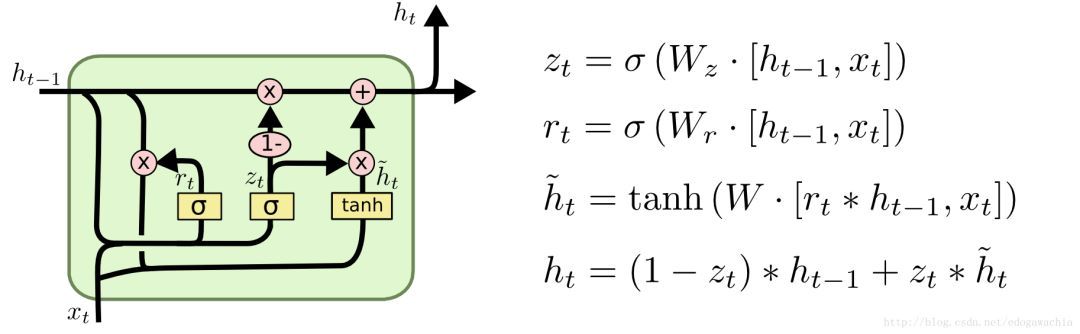
从这个图的公式来看,r和z就是两个门,分别表示reset和update。(此图的公式和论文Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation 中的公式略有出入,见下图,个人以为此图更好,因为逻辑上讲update越大应该更新的内容,也就是选择的candidate的内容越多)
GRU的基本原理是,首先,用x(t)和h(t-1)生成两个门,然后用reset门乘以上一时刻的状态,看看是否要reset或者reset多大程度,然后,和新输入的x拼接,过网络并用tanh激活,形成candidate的隐含变量hat{h_t},然后,将上一时刻的h和candidate的h做一个线性组合,两者的权重和为1,candidate的权重就是update门的输出,表征更新强度多大。
要注意的是,h只是一个变量,因此在每个时刻,包括最后的线性组合,h都是在用以前的自己和当前的备选答案更新自己。举例来说,这一个变量好比一杯酒,每次我们要把一部分酒倒出去,并把倒出去的酒和新加入的原料混合,然后在倒回来,这里的reset控制的就是要倒出去的,并且混合好之后再倒回来的酒的比例,而update控制的则是用多大的比例混合新原料和倒出来的之前调制好的酒。同理,也可以以此理解LSTM,LSTM的遗忘门功能上和reset相似,而输入门与update相似,不同之处在于LSTM还控制了当前状态的exposure,也就是输出门的功能,这是GRU所没有的。
GRU参数少,好训练,结构相对简单一些。对于上图展示的GRU公式,如果reset = 1,update = 1,那么就变成了一个plain RNN。实际上,有测试表明,RNN各种变体之间性能上相差不大,基本相同。
与lstm相比,从直观上我们可以看到“门”由三个变为两个,论文中称为重置门和更新门。同时,也少了ct这个状态变量。
gru中通过1-zt倍的ht-1选择记住部分过去信息,通过zt倍的ht(~)选择记住部分当前信息,相加为当前step的输出信息。与lstm的核心原理相同,gru也是选择记住一定比例的过去的信息和一定比例的现在的信息,但在比例的选择上呈现差异,lstm对过去和现在的信息选择相同的比例输出,而gru对过去和现在的信息输出的比例和为1,对输出的过去信息和现在信息有一种权重的作用。
核心区别在于gru在计算当前state信息时对过去信息有一种选择性,即当前信息的产生是否受过去信息的影响。

