CF1581B Diameter of Graph（思维，构造，树）

原题链接

题意

给 $n$ 个点，$m$ 条边，要求你这样构成一个无向连通图，使任意两点之间的最短距离小于 $k?1$。

思路

分类讨论。

小于 $k?1$ 实际上就是 小于等于 $k?2$。

1. 如果 n == 1，m == 0 时是 YES，同时还要满足 $k>=2$，因为距离如果小于 $0$ 的话，就不合理了。

2. 要想构成一个无向连通图，那么边数至少需要 $n?1$ 条， 可以发现有 $n?1$ 条边时，任意两点最短距离的长度已经是 $2$ 了。此时 $k$ 的取值范围可以是 $k>=4$。

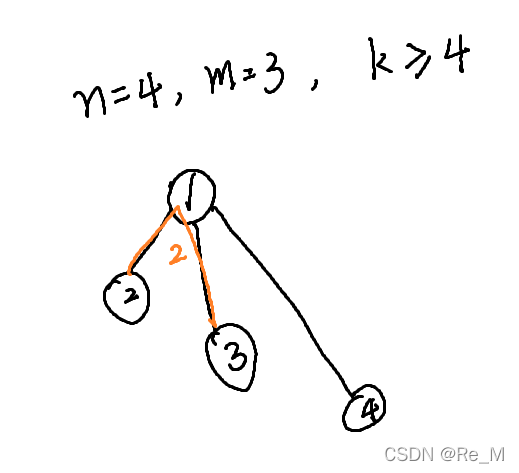
3. 要想任意两点长度为最短的 $1$，需要继续加边。可以发现再每两点之间都连一条边可以实现，那么共有 $(1+n?1)?(n?1)/2$ 条边，此时的 $k$ 的取值范围就是 $k>=3$。

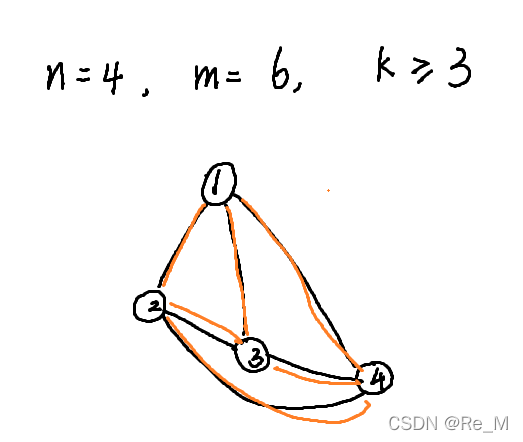
4. 这个无向连通图不能有重边和自环，那么最多就只能有上图那么多条边，也就是 $(1+n?1)?(n?1)/2$ 条边。所以边数大于 $(1+n?1)?(n?1)/2$ 的都是错的。
5. 其余情况就都是错的。

代码

#include<bits/stdc++.h> 
#define int long long
using namespace std;
signed main()
{
    int t;cin >> t;while (t -- ){
    int n, m, k;cin >> n >> m >> k;bool f = 0;if (n == 1 && m == 0 && k >= 2) f = 1;if (m < (1 + n - 1) * (n - 1) / 2 && m >= n - 1 && k >= 4) f = 1;if (m == (1 + n - 1) * (n - 1) / 2 && k >= 3) f = 1;if (f) cout << "YES" << endl;else cout << "NO" << endl;}return 0;
}

总结

本题难点：

1. 读懂题目
2. 判断出每种情况。

勤加练习，提升思维能力！