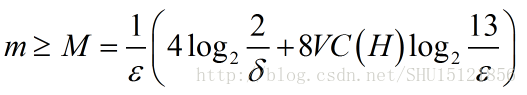PAC的意思
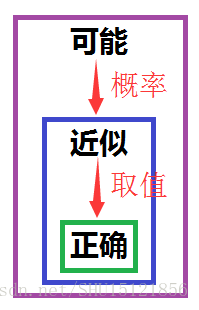
Probably Approximate Correct直译过来就是”可能近似正确”,这里面用了两个描述”正确”的词,可能和近似。
“近似”是在取值上,只要和真实值的偏差小于一个足够小的值就认为”近似正确”;”可能”是在概率上,即只要”近似正确”的概率足够大就认为”可能近似正确”。
泛化误差随学习复杂性变大
上节查漏补缺中了解到了,如果训练集不是很大,也就是用来给学习机器学习的样本数量比较有限的情况下,如果过于追求让经验风险小,学习复杂性太高,会导致过学习现象,也就是学习出来的模型的推广能力变差,这可以用泛化误差变大来表征。
机器学习所做的事情
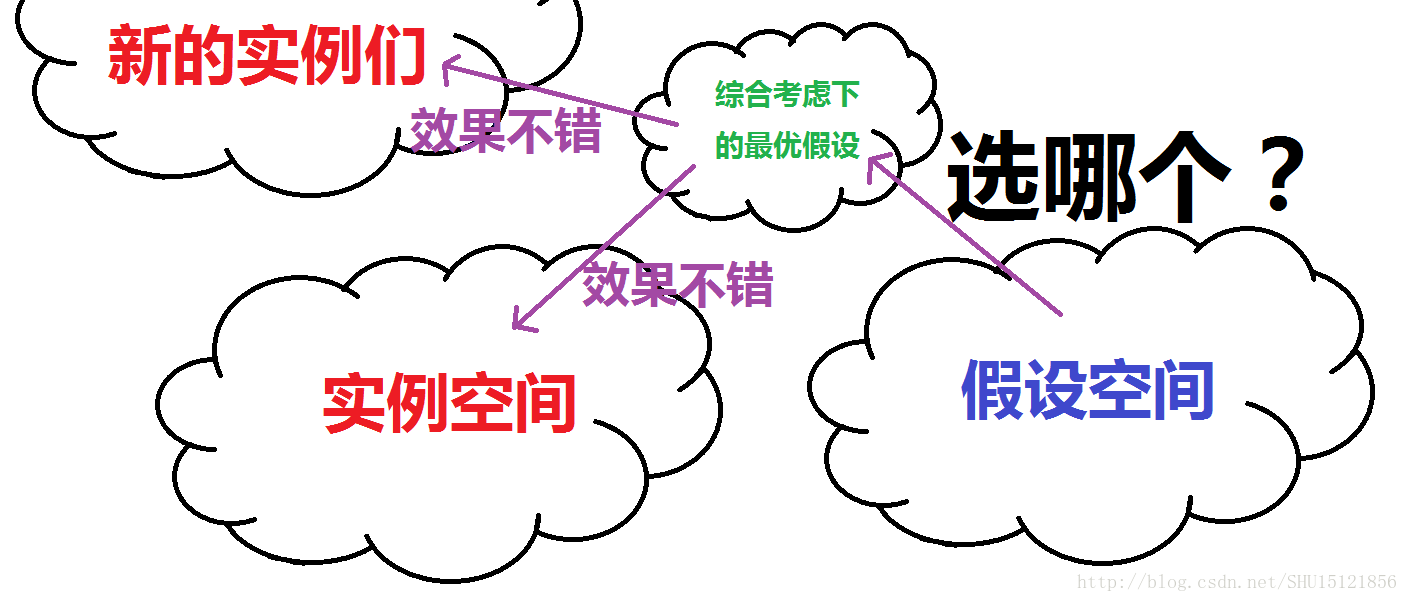
先看看到现在为止理解的,机器学习所做的事情是,从假设空间(暂时理解成要选择的函数集/模型集)中选取一个假设(暂时理解成函数/模型),对于训练集中的样本能较好的完成任务,并且对于外来的样本,也能较好的完成任务(泛化误差较小)。这样学习到的学习机器才是一个有效的模型。
PAC所做的事情
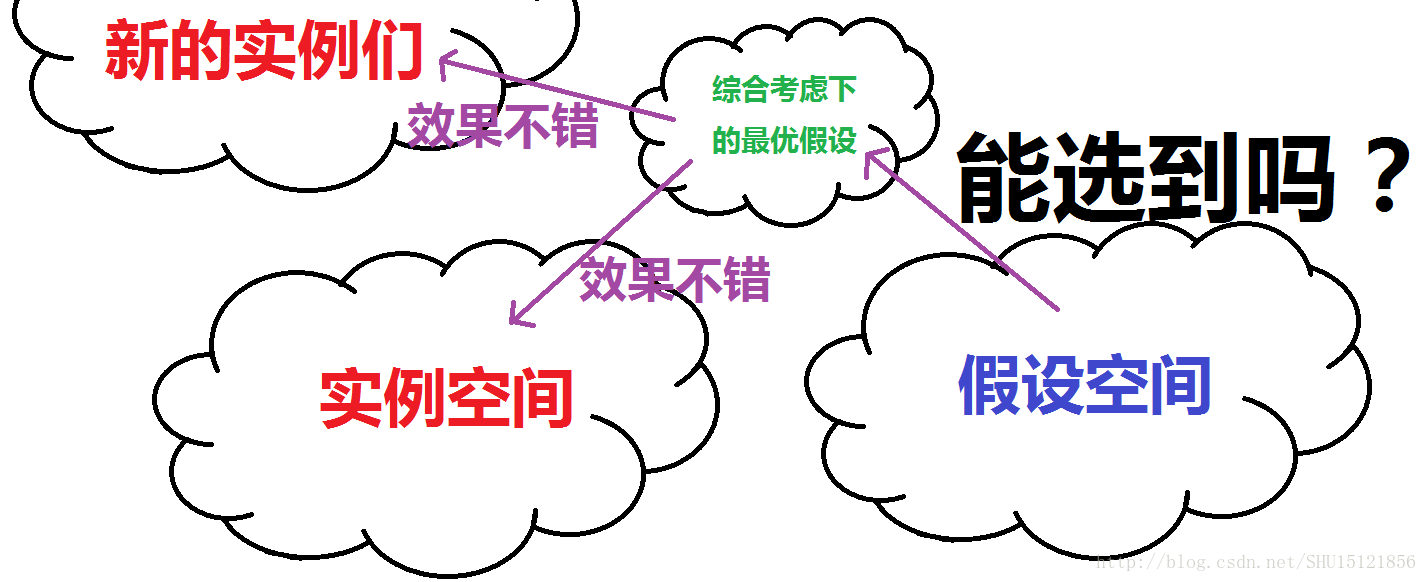
上面那张图能看出来,机器学习关心的是从假设空间中以什么样的方式选出的假设才是最优的,也就是选哪个。而PAC关心的是能不能从假设空间空选出一个最优的假设,也就是说在这样有限的训练集下,能不能在假设空间中找到一个好的假设来完成任务。也就是说PAC可以用来判断达没达到可以选择出足够好的假设来解决问题的下限。
以近似正确(AC)代替正确(C)
如果是完全意义上的正确,那么肯定是对实例空间里的样本经验风险为0,同时又对外来的实例泛化误差为0,这显然是不可能的。而且经验风险太小也不是一件好事(过学习从而推广能力下降),所以只要设定一个阈值,只要选取出的假设h的泛化误差E(h)不超过这个值(即近似正确)就认为是”正确”的了,而不是去追求完全的”正确”。
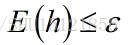
以可能近似正确(PAC)代替近似正确(AC)
实际上,对于所有外来的实例,假设h都能做到”近似正确”,这也几乎是不可能的一件事。只要对于多数的外来实例,都能做到”近似正确”,也就是说设定一个概率的阈值,只要”近似正确”的频率不小于这个概率阈值(即可能近似正确),就认为是”近似正确”的了,而不是去追求对所有训练集外的实例都”近似正确”。
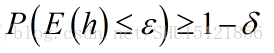
这里常常给出显著性水平,也就是说只要机器学习对外来的随机样本失败的频率被限定在这个值以内。用总的概率1减去它就是置信度,作为判断”可能近似正确”的阈值。
PAC可学习
如果学习机器在短时间(多项式级别)内根据少量的(多项式级别)的训练集样本m,能够找到一个好的假设h,满足上面的那个式子,那么就说这个问题是PAC可学习的。
一般理论边界
显然在给定的泛化误差和显著性水平,一个PAC可学习的问题也必须要有足够多的样本m才能完成任务,而这个样本数m有一个一般理论边界M,如果m大于M那么就足以在预期的泛化误差和显著性水平下用机器学习找到的最优的假设h解决问题。
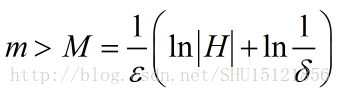
这里|H|表示假设空间的大小。这个式子的意思可以这样理解,在这个问题下训练样例的数目如果是m,足以保证机器学习得到的最优假设h是可能(置信度是1-δ)近似(泛化误差是ε)正确的。
一般理论边界的局限性
这个式子局限性还很大,一方面M只是m的一个上界,而且可能还比较宽松,对于m<=M也不见得PAC不可学习;另一方面|H|是假设空间的大小,单纯地用它刻画样本复杂度不够合理(显然样本复杂度凭什么随着假设空间的大小线性增长呢),对于无限假设空间的情形显然这个式子完全失效。
函数集的VC维
这里的指示函数可以理解成能指示这个结果属于哪个类别的函数,比如结果为0或1表示两个类别。如果是有界的实函数,可以设定一个阈值,那么就可以根据函数结果转换成二分类的指示函数。
如果问题给的实例只要分成2类,那么对于一个指示函数集H,如果m个样本能被H中的函数按照所有可能的2^m种方式区分开,那么就说这个函数集能把m个样本打散。
函数集H的VC维VC(H)也就是它所能打散的最大样本数目。很显然对于有限的函数集H,VC维有界:
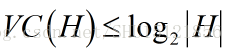
这很好理解,试想这|H|个函数每个都能产生一种互异的二分类方式,也就有了|H|种二分类方式,而有|H|种二分类方式的样本最多也就是以2为底|H|的对数这么多个了,所以VC(H)绝不会超过它。
一个用烂了的例子
目前没有通用的关于任意函数VC维计算的方法,对一些特殊的函数知道其VC维。这个平面上的点被线性决策线二分类的例子到处都是,可以用来理解一下VC维。
假如函数集H是平面上的所有线性决策线(其实也就是直线,但是根据把点分成两边能做二分类所以叫线性决策线),显然|H|=+∞。给定的实例是平面上的点,现在用线性决策线尝试把给定的一些点打散。
对于3个以内的点,还是能打散的:
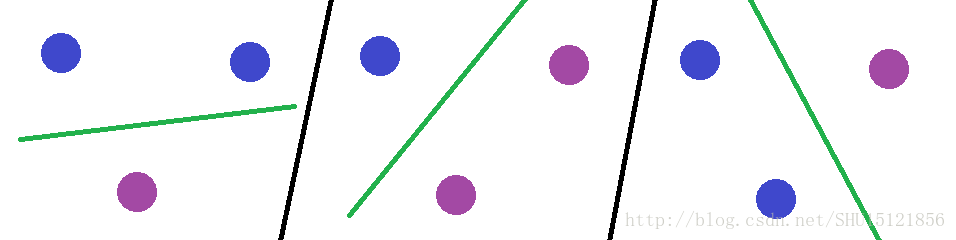
而对于4个样本点,就不能打散了,试想要把下图中的两个紫色点分到一起,线性决策线做不到:

所以这个问题的VC维VC(H)=3。
VC维衡量假设空间复杂度
用VC维代替前面的|H|来刻画假设空间下的样本复杂度,不仅能够把边界M做的更紧凑,而且可以去刻画无限假设空间下的样本复杂度。这时候新的PAC可学习边界: