算法
所谓 算法 (algorithm)就是定义良好的计算过程,它取一个或一组值作为 输入 ,并产生出一个或一组值作为 输出 。亦即,算法就是一系列的计算步骤,用来将输入数据转换成输出结果。我们还可以将算法看作是一种工具,用来解决一个具有良好规范说明的 计算问题 。
例如,假设要将一列数按非降顺序进行排列,下面是有关该排序问题的形式化定义:
输入 :由 n 个数构成的一个序列<a1, a2, …, an>
输出 :对输入序列的一个排列(重排)<a1 ', a2 ', …, an '>使得a1 ' <= a2 ' <= … <= an '
插入排序
插入排序 算法是一个对少量元素进行排序的有效算法。它的伪码是以一个过程的形式给出的,称为 INSERTION-SORT ,它的参数是一个数组 A [ 1 .. n ],包含了 n 个待排数字。(在伪码中, A 中元素的个数 n 用 A.length 来表示。)输入的各个数字是 原地排序 的(sorted in place),就是说这些数字是在数组 A 中进行重新排序的,在任何时刻,至多只有其中的常数个数字是存储在数组之外的。当过程 INSERTION-SORT 执行完毕后,输入数组 A 中就包含了已排好序的输出序列。
INSERTION-SORT(A) 1 for j = 2 to A.length 2 key = A[j] 3 // Insert A[j] into the sorted sequence A[1 .. j - 1] 4 i = j - 1 5 while i > 0 and A[i] > key 6 A[i + 1] = A[i] 7 i = i - 1 8 A[i + 1] = key
插入排序算法的简单Java实现:
/*** 插入排序** @param array*/
public static void insertionSort(int[] array) {int key, j;for (int i = 1; i < array.length; i++) {key = array[i];j = i - 1;while (j >= 0 && array[j] > key) {array[j + 1] = array[j];j--;}array[j + 1] = key;}
}
循环不变式与插入算法的正确性
下图给出了这个算法在数组 A = <5, 2, 4, 6, 1, 3>上的工作过程。下标 j 指示了待插入的元素。在外层 for 循环的每一轮迭代开始时,包含元素 A [ 1 .. j - 1 ]的子数组就已经是排好序的了。
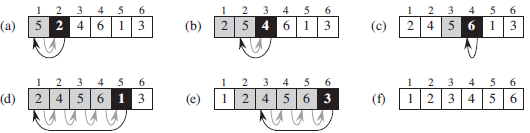
循环不变式 主要用来帮助我们理解算法的正确性。对于循环不变式,必须证明它的三个性质:
初始化(Initialization):
它在循环的第一轮迭代开始之前,应该是正确的。
保持(Maintenance):
如果在循环的某一次迭代开始之前它是正确的,那么,在下一次迭代开始之前,它也应该保持正确。
终止(Termination):
当循环结束时,不变式给了我们一个有用的性质,它有助于表明算法是正确的。
算法分析
算法分析 是指对一个算法所需要的资源进行预测。内存,通信带宽或计算机硬件等资源偶尔会是我们主要关心的,但通常,资源是指我们希望测度的计算时间。
插入排序算法的分析
INSERTION-SORT 过程的时间开销与输入有关。此外,即使排序两个相同长度的输入序列,所需的时间也可能不同。这取决于它们已排序的程度。一般来说,算法所需的时间是与输入规模同步增长的,因而常常将一个程序的运行时间表示为其输入的函数。这里就涉及到两个名词“运行时间”和“输入规模”。
输入规模 的概念与具体问题有关,最自然的度量标准是输入中的元素个数。
算法的 运行时间 是指在特定输入时,所执行的基本操作数(或步数)。这里我们假设每次执行第 i 行所花的时间都是常量 ci 。
首先给出 INSERTION-SORT 过程中,每一条指令的执行时间及执行次数。对 j = 2, 3, …, n , n = A.length ,设 tj 为第5行 while 循环所做的测试次数。当 for 或 while 循环以通常方式退出时,测试要比循环体多执行1次。另外,假定注释部分不可执行。

该算法总的运行时间是每一条语句执行时间之和。为计算总运行时间 T = [ n ],对每一对 cost 和 times 之积求和。得:

即使是对给定规模的输入,一个算法的运行时间也可能要依赖于给定的是该规模下的哪种输入。例如,在 INSERTION-SORT 中,如果输入数组已经是排好序的,那就会出现最佳情况。对 j = 2, 3, …, n 中的每一个值,都有 tj = 1,则最佳运行时间为:
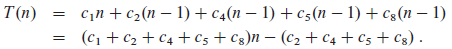
这一运行时间可以表示成 a n + b ,常量 a 和 b 依赖于语句的代价 ci ;因此,它是 n 的一个 线性函数 。
如果输入数组是按照逆序排序的,那么就会出现最坏情况。我们必须将每个元素 A [ j ]与整个已排序的子数组 A [ 1 .. j - 1 ]中的每一个元素进行比较,因而,对 j = 2, 3, …, n ,有 tj = j 。则最坏运行时间为:
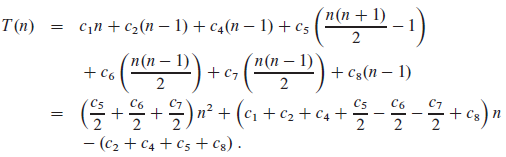
这一最坏情况运行时间可以表示为 a n2 + b n + c ,常量 a , b 和 c 仍依赖于语句的代价 ci ;因而,这是一个关于 n 的 二次函数 。
练习
2.1-2
重写过程 INSERTION-SORT ,使之按非升序排序。
INSERTION-SORT(A) 1 for j = 2 to A.length 2 key = A[j] 3 // Insert A[j] into the sorted sequence A[1 .. j - 1] 4 i = j - 1 5 while i > 0 and A[i] < key 6 A[i + 1] = A[i] 7 i = i - 1 8 A[i + 1] = key
2.1-3
考虑下面的查找问题:
输入 :一列数 A = <a1, a2, …, an>和一个值/v/ 。
输出 :下标 i ,使得 v = A [ i ],或当 v 不在 A 中时为 NIL 。
写出线性查找的伪码:
LINEAR-SEARCH(A, v) 1 for j = 1 to A.length 2 if A[j] == v 3 return j 4 return NIL
2.1-4
将两个各存放在数组 A 和 数组 B 中的 n 位二进制整数相加。和以二进制形式存放在具有 n + 1个元素的数组 C 中。
ADD-BINARY-ARRAY(A, B) 1 let C[1 .. A.length + 1] be new arrays 2 flag = 0 3 for i = 1 to A.length 4 key = A[i] + B[i] + flag 5 C[i] = key mod 2 6 if key > 1 7 flag = 1 8 else 9 flag = 0 10 C[i] = flag
2.2-2
选择排序 伪码:
SELECT-SORT(A) 1 for i = 1 to A.length - 1 2 index = i 3 for j = i + 1 to A.length 4 if A[index] > A[j] 5 index = j 6 exchange A[index] with A[i]