1.①张量
在某些情况下,我们会讨论坐标超过两维的数组。一般地,一个数组中的元素分布在若干维坐标的规则网格中,我们称之为张量。
②矩阵乘积运算
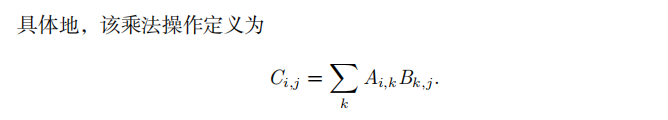
为 元素对应乘积(element-wise product)或者 Hadamard 乘积(Hadamard product),记为 A ⊙ B
一个列向量线性相关的方阵被称为 奇异的(singular)。
2.范数
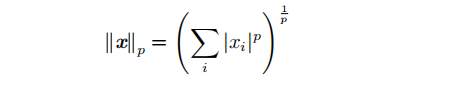
范数(包括 Lp 范数)是将向量映射到非负值的函数。直观上来说,向量 x 的范数衡量从原点到点 x 的距离。更严格地说,范数是满足下列性质的任意函数:




3.对角矩阵的性质
对角矩阵受到关注的部分原因是对角矩阵的乘法计算很高效。计算乘法 diag(v)x,![]()
![]() (矩阵求逆矩阵)
(矩阵求逆矩阵)
特殊的性质;
矩阵之间的正交性 ;标准正交(单位长为1);正交矩阵的求逆运算(直接求转置,计算代价小)
4.特征向量

假设矩阵 A 有 n 个线性无关的特征向量 {v(1), . . . , v(n)},对应着特征值{λ1, . . . , λn}。我们将特征向量连接成一个矩阵,使得每一列是一个特征向量:
