基础知识
条件概率(Conditional Probability)


相互独立时,p(A | B) = p(A)
贝叶斯规则
贝叶斯网络(Bayesian Network)定了一个独立的结构:一个节点的概率仅依赖于它的父节点。贝叶斯网络适用于稀疏模型,即大部分节点之间不存在任何直接的依赖关系。
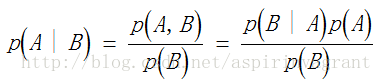

联合概率(Joint Probability),表示所有节点共同发生的概率,将所有条件概率相乘:
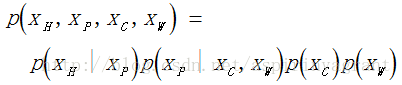
我们最终的目标是计算准确的边缘概率(Marginal Probability),比如计算Hangover的概率,边缘概率为各种状态下所有其他节点对本节点影响的概率的和。
边缘概率(Marginal Probability):即某个事件发生的概率,而与其它事件无关。边缘概率是这样计算的:在联合概率中,把最终结果中不需要的那些事件合并成其事件的全概率而消失(在两个离散随机变量的条件下,对于其中任一行或任一列求和,得到的概率就是边缘概率)。在本例中,针对不同的Hangover进行求和,得到的就是Hangover的边缘概率:
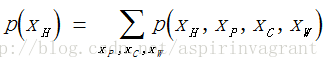
优化
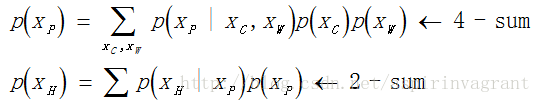
接下来就是要获得观测变量 xh 的估计,需要使 p(xh)的值最大, 即:
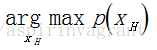
如果贝叶斯网络比较小,我们可以很简单的做边缘求和运算,但是如果问题规模较大,整个运算复杂度和数据将会以指数级增长。而利用BP算法去计算这样的网络问题,可以使得运算复杂度只和节点数线性相关。在这种意义上,BP算法在大型贝叶斯网络推断问题中扮演着越来越重要的作用。
马尔科夫随机场(Markov Random Field,MRF)
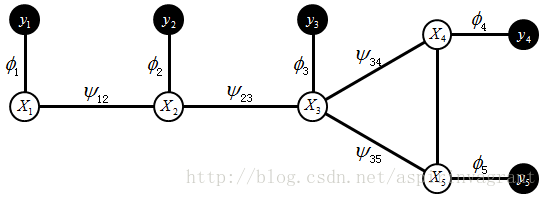
在概率图模型中,每个结点表示一个随机变量,结点之间的边表示这些随机变量之间的概率关系。在概率图模型中,所有随机变量的联合概率分布可以表示成若干随机变量子集的乘积。典型的概率图模型包括贝叶斯网和马尔科夫网。贝叶斯网是有向图模型,用于表示随机变量之间的因果关系,而马尔科夫网是无向图模型,用于表示随机变量的概率分布和概率推理,或者说是随机变量之间的软约束关系。
BP算法的基础就是建立于MRF上,MRF是一种条件概率模型,它可以被认为是马尔科夫链的一种推广,其对于场内所有节点的相关性都能很有效的描述。
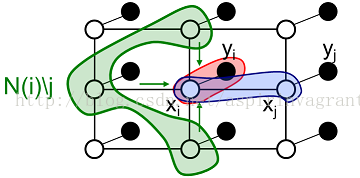
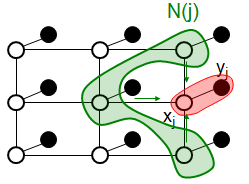
假设我们观察到yi的一些信息,需要利用这些已知信息去推断关于隐含的场景xi的另外一些信息。每个顶点i都有一个状态值xi和一个观测值yi,每个状态值和观测值之间的似然函数为Фi(xi,yi),反映了i处的 xi和 yi存在统计依赖性,表示节点i的联合相容度,相邻邻居节点之间的势能量为Ψij(xi,xj),Ψij(xi,xj)也称为相邻节点之间的不连续代价,反映了节点变量 xi 和 xj 之间的相容性,体现了随机场自身具备的约束条件。
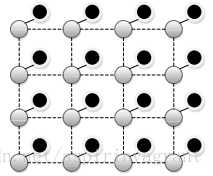
灰色点表示隐含节点xi,黑色点表示显式节点yi,实线表示存在似然函数Фi,虚线表示存在一对势函数Ψij和Ψji。
联合概率为:

其中,Z 是一个归一化常数。
边缘概率为:
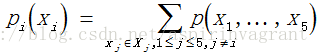
马尔科夫随机场被认为是成对的,正是因为隐含节点和显式节点的成对性,而每一对节点中的隐含节点的似然函数只受其对应的显式节点所影响。成对的MRF相比较与贝叶斯网络来说它是非直接的。同样的,直接计算边缘概率同样也会导致时间上的指数级增长。
置信度传播(Belief Propagation,BP)
置信度传播算法利用结点与结点之间相互传递信息而更新当前整个MRF的标记状态,是基于MRF的一种近似计算。该算法是一种迭代的方法,可以解决概率图模型概率推断问题,而且所有信息的传播可以并行实现。经过多次迭代后,所有结点的信度不再发生变化,就称此时每一个结点的标记即为最优标记,MRF也达到了收敛状态。对于无环环路的MRF,BP算法可以收敛到其最优解。
BP算法的两个关键过程:(1)通过加权乘积计算所有的局部消息;(2)节点之间概率消息在随机场中的传递。

置信度替换为概率:
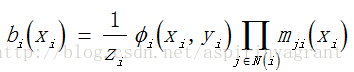
bi(xi)为节点i的联合概率分布,其中mji(xi)代表隐含节点j传递给隐含节点i的消息,表明了隐含节点i对隐含节点j当前状态的影响。Фi(xi,yi) 表示节点i的局部证据,表示节点i的联合相容度。节点i的置信度bi(xi)与 i 的邻域向 i 传递的所有消息的乘积成正比,同时也正比于Фi(xi,yi) ,1/zi为归一化常数,可使置信度的和为1,N(i) 为节点i的MRF一阶邻域。
消息传播的信息:
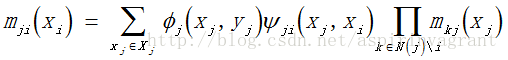
包含所有其他传入节点i的消息乘积,N(j)\i表示节点j的MRF一阶邻域中排除掉目标节点i的邻域。
有了消息更新规则以及置信度计算公式,就可以先任意初始化每个bi(xi),然后迭代的求解mij和bi(xi)直至收敛,也就是说mij不再发生变化。也就是说首先对一些初始节点的消息赋初值,然后多次迭代消息传播和置信度更新直到它们稳定,最后就能从置信度中获取相应的概率。
置信度传播算法中迭代运算步骤可以表示如下:
(1)随机选择相邻的隐含节点xi,xj
(2)从xi向xj发送消息mij
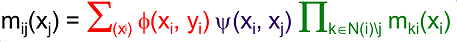
(3)更新节点xj的置信度
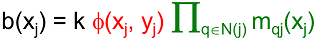
(4)跳至步骤(1),直到算法收敛
在以此为规则的计算中,从无环图的边缘节点开始传播,然后如果一个节点所有相邻节点的消息都已经计算出来,则计算该节点的消息。易得整个无环图仅仅只需计算一遍就可以得到所有隐含节点的边缘概率分布。可以看出,BP 算法相对于一般的算法,时间复杂度上是大幅下降的。
标准最大乘置信度传播算法

举例:
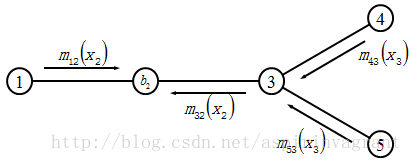
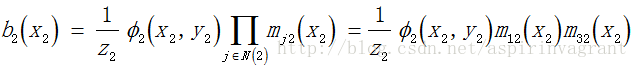
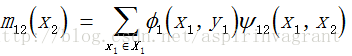
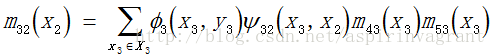
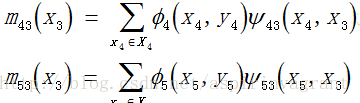
通过整理上述公式,就可以得到节点2的置信度,正好就是节点2的边缘概率:b2(x2)= p2(x2)。
参考资料:
Understanding Belief Propagation and itsGeneralizations
CRF - Conditional Random Fields
Structured Belief Propagation for NLP