文章目录
-
- 摘要
- 引言
- 具体方法介绍
-
- 参数定义:
- sentence encoder
- Selective Attention over Instances
- 总结
摘要
现存问题:远程监督会出现一些错误标注的问题
解决方法:使用卷积神经网络映射句子语义,使用attention机制减少噪声 数据的权重。
实验证明和意义:模型可以利用句子的所有信息,并且减少错误样本的影响。
引言
现状:
针对KB,现有实体跟现实世界的实体差很远很远。因此自动的关系抽取很重要(因为可以不依赖现有实体去做)。
介绍他人工作:
目前大多数关系抽取都是基于大量的人工标注有监督学习。
其基于以下假设(也是远程监督的定义):
如果两个实体在KB中某关系,那么所有的包含该实体对的句子都表达这该关系
显然,很容易出现反例。传统方法的缺陷在于它不是一个end-to-end的系统,它总依赖于tag,pos等一系列的操作。误差就会由此传播。
引入深度学习的概念,其中最接近的一篇工作的思想是:
至少存在一个包含那些实体的句子会表现出它们的关系。然后为每个实体对只选择最有可能的句子来进行训练和预测
显然只选择最有可能的句子,会丢失其他句子的意义
自己的工作:
-
提出基于距离的卷积神经网络(CNN),用于远程监控关系的提取。
-
在多个实例上建立了句子级别的关注(动态减少那些噪声实例的权重)。
-
利用句子层次的注意力机制,提取与关系向量的关系。
具体方法介绍
参数定义:
word:x={w1,w2..wm}x=\{w_1,w_2..w_m\}x={
w1?,w2?..wm?}(一个句子含有m个词)
sentence:{x1,x2,x3...}\{x_1,x_2,x_3...\}{
x1?,x2?,x3?...}
relation:r
vocabulary size:V
词嵌入的维度:a
位置距离的维度:b
词向量维度:d
句子向量维度:dcd^cdc
卷积窗口长度:l
卷积核:WjW_jWj?
句子全集:S
sentence encoder
word representation
- word embeddings: 普通的词嵌入模型
- position embeddings:帮助CNN keep trace每个词离前后实体的位置(2个实数,前和后)
因此最终word vector(这里还是词不是句子):
wi∈Rd(d=da+db×2)w_i\in R^d(d=d^a+d^b\times2)wi?∈Rd(d=da+db×2)
其中a是词嵌入的维度,b是位置距离的维度
Convolution,Max-pooling and Non-linear layers
引入卷积和max-pooling的作用(跟该任务其实无关,这跟当初为什么NLP引入卷积有关,这是一个通用的作用)。
维度解释很重要
卷积核:W∈Rdc×(l×d)W\in R^{d^c\times (l \times d)}W∈Rdc×(l×d)
卷积窗口:qi=Rl×dq_i=R^{l\times d}qi?=Rl×d
qi=wi?l+1:iq_i=w_{i-l+1:i}qi?=wi?l+1:i?
就是l窗口内,由上一步得到的各个词的向量拼接(水平)
因此第i个滤波器对应的feature map是:
pi=[Wq+b]ip_i=[Wq+b]_ipi?=[Wq+b]i?
注意这里q没有下标,实际上应该是(dc×l×d)X(l×d×m)(d_c \times l\times d)X(l \times d \times m)(dc?×l×d)X(l×d×m),这个m就是窗口的数量,跟句子的词数长度成正比。
因此就需要进行池化:
[x]i=max(pi)[x]_i=max(p_i)[x]i?=max(pi?)
最后接一个非线性函数tanh,relu之类的在输出处。
具体的过程就如下:
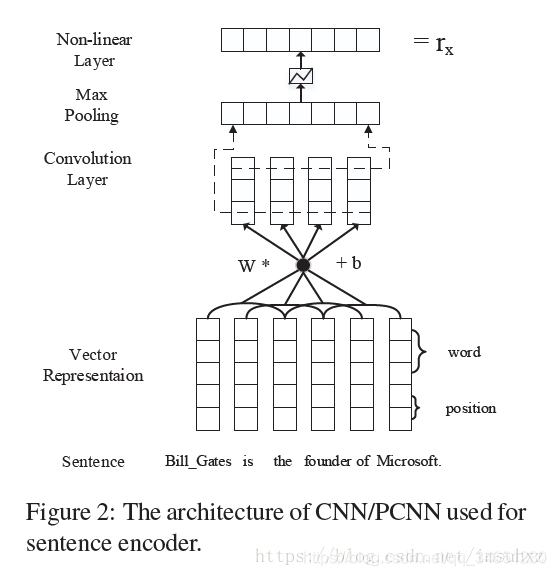
Selective Attention over Instances
输入:
- 包含特定实体的句子集合S
- 该句子集合经过第一部分得到向量表示。S={x1,x2,x3}\{x_1,x_2,x_3\}{ x1?,x2?,x3?}
小目标:希望得到得分概率表示P(r∣S,θ)P(r|S,\theta)P(r∣S,θ)(即在S实体对下,r的得分)
因此就需要对集合S进行整合为a real-valued vector s :
- 采用平均权重
- 采用注意力机制
过程:
ei=xiAre_i=x_iArei?=xi?Ar
αi=exp(ei)∑kexp(ek)\alpha_i=\frac{exp(e_i)}{\sum_k exp(e_k)}αi?=∑k?exp(ek?)exp(ei?)?
s=∑iαixis=\sum_i \alpha_ix_is=i∑?αi?xi?
o=Ms+do=Ms+do=Ms+d
P(r∣S,θ)=exp(or)∑k=1nrexp(ok)P(r|S,\theta)=\frac{exp(o_r)}{\sum_{k=1}^{n_r}exp(o_k)}P(r∣S,θ)=∑k=1nr??exp(ok?)exp(or?)?
其中,A是一个权重对角矩阵,r是代表着该关系的向量,e实际上就是注意力评分函数,与该实体关系更加密切的句子可以取得更大的取值。
总结
这篇文章的贡献在于传统观点,认为两个实体存在某种关系,那么所有包含该实体对的句子都表示这种关系,但是存在噪声,文章利用注意力机制对包含该实体对的各个句子进行权重的学习,使得其更好的表现该关系。