目录
标量、向量、矩阵、张量的关系
Scalar(标量)
Vector(向量)
Matrix(矩阵)
Tensor(张量)
Array(数组)
标量、向量、矩阵、张量的关系
先上几张图感受下,Scalar - Vector - Matrix - Tensor其实就是数据维度逐渐上升的过程。

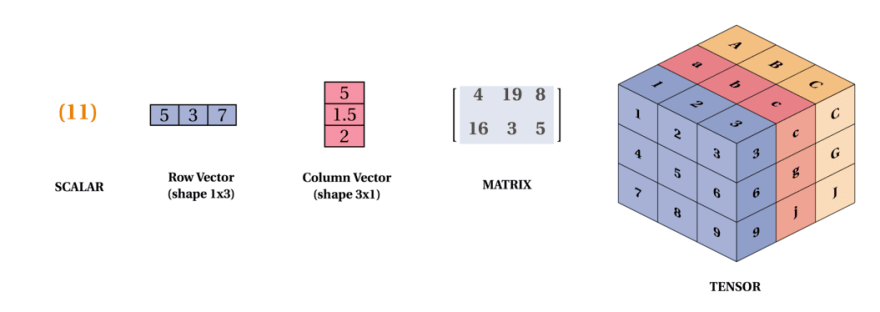
点——标量(scalar)
线——向量(vector)
面——矩阵(matrix)
体——张量(tensor)
Scalar(标量)
标量只有大小概念,没有方向的概念。通过一个具体的数值就能表达完整。
比如:重量、温度、长度、提及、时间、热量等都数据标量。
Vector(向量)
物理学上也叫矢量,指由大小和方向共同决定的量(跟「标量」相区别)。如力、速度等。
向量主要有2个维度:大小、方向。
大小:箭头的长度表示大小;
方向:箭头所指的方向表示方向。
Matrix(矩阵)
矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合,元素是实数的矩阵称为实矩阵,元素是复数的矩阵称为复矩阵。
而行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵。
由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵,简称m × n矩阵。记作:

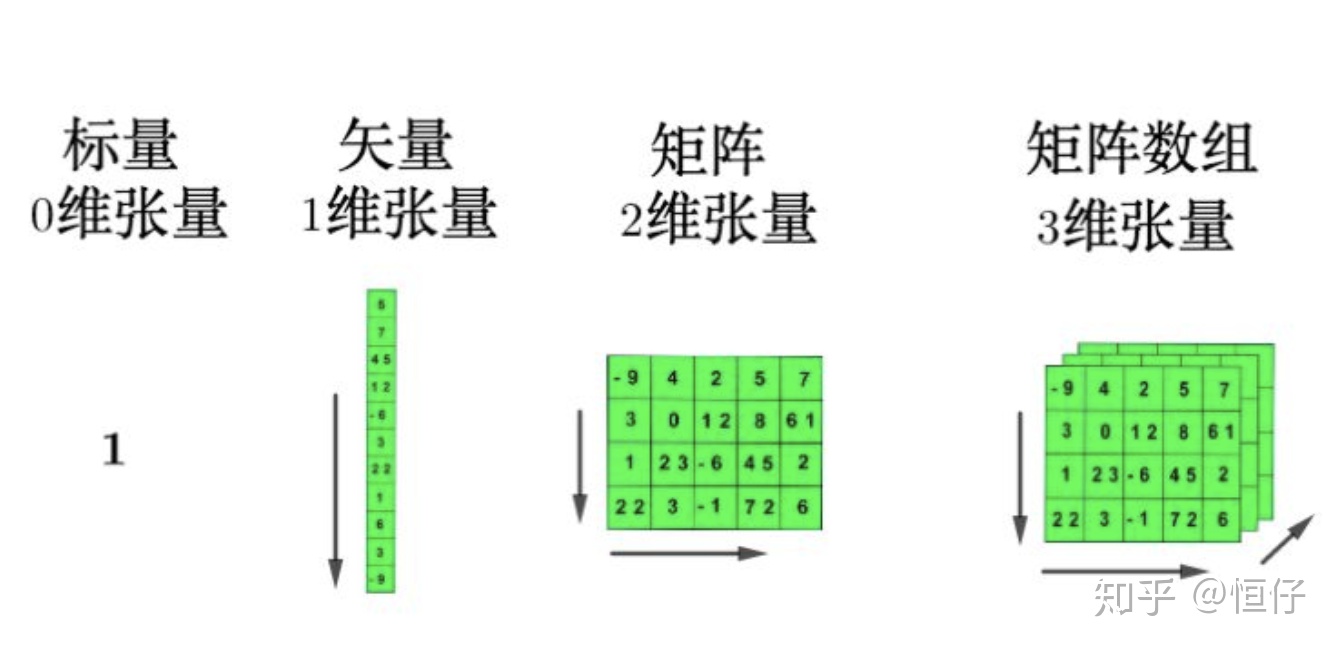
Tensor(张量)
A tensor is a generalization of vectors and matrices to potentially higher dimensions.
Tensor实际上就是一个多维数组(multidimensional array),其目的是能够创造更高维度的矩阵、向量。
Tensor对象的3个属性:
- rank:number of dimensions 维度
- shape: number of rows and columns 行列数
- type: data type of tensor's elements 元素类型
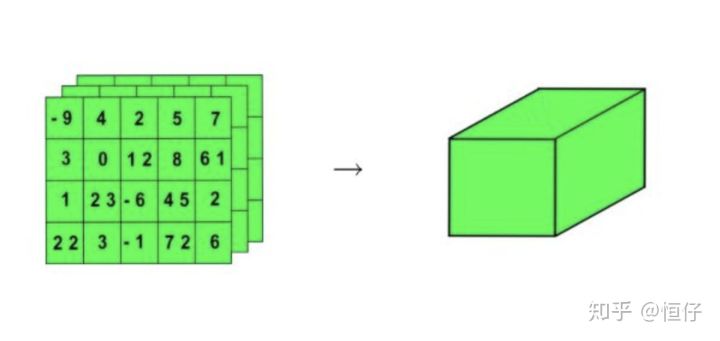
现在将三维的张量用一个正方体来表示
一个量, 在不同的参考系下按照某种特定的法则进行变换, 就是张量。
额外补充:Array(数组)
数组是类似于列表的高阶对象,是有序的元素序列。我们经常在Numpy里对数组进行运算。
Python也有数组,为什么要用Numpy?
- Python中提供了list容器,可以当作数组使用。但列表中的元素可以是任何对象,因此列表中保存的是对象的指针,这样一来,为了保存一个简单的列表[1,2,3]。就需要三个指针和三个整数对象。对于数值运算来说,这种结构显然不够高效。
- Python虽然也提供了array模块,但其只支持一维数组,不支持多维数组,也没有各种运算函数。因而不适合数值运算。
- Numpy内置丰富的方法,能更加轻松高效地进行科学计算。