NYOJ - 301 - 递推求值 ( 递推+矩阵快速幂 )

给你一个递推公式：

f(x)=a*f(x-2)+b*f(x-1)+c

并给你f(1),f(2)的值，请求出f(n)的值，由于f(n)的值可能过大，求出f(n)对1000007取模后的值。

注意:-1对3取模后等于2

输入

第一行是一个整数T,表示测试数据的组数(T<=10000)
随后每行有六个整数，分别表示f(1),f(2),a,b,c,n的值。
其中0<=f(1),f(2)<100,-100<=a,b,c<=100,1<=n<=100000000 (10^9)

输出

输出f(n)对1000007取模后的值

样例输入

2
1 1 1 1 0 5
1 1 -1 -10 -100 3

样例输出

5
999896

矩阵递推式（不唯一）：

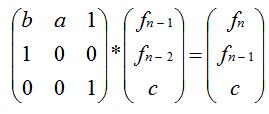
矩阵T是左边3*3的矩阵，矩阵A是左边3*1的矩阵，由递推矩阵可以看出 f n可以通过 矩阵 T 乘以 矩阵 A 获得 

如果 给出 f1 和 f2 乘以一次矩阵T 求出的是 f3 

所以当要求fn 的时候  求的是 T^(n-2) * A ;

#include<cstdio>
#include<cstring>
#define LL long long 
#define MOD 1000007
using namespace std;int t ;
LL k,a,b,c,f1,f2;
struct Matrix{LL v[3][3];Matrix(){memset(v,0,sizeof(v));}
}; //乘法 
Matrix mul(Matrix x,Matrix y){Matrix ans;for(int i=0 ;i<3 ;i++){for(int j=0 ;j<3 ;j++){for(int k=0 ;k<3 ;k++){ans.v[i][j] =  (ans.v[i][j]+x.v[i][k]*y.v[k][j])%MOD;}}}return ans;
} //快速幂
Matrix q_pow(Matrix m,LL k){//单位矩阵初始化 Matrix ans;ans.v[0][0] = 1; ans.v[0][1] = 0; ans.v[0][2] = 0;ans.v[1][0] = 0; ans.v[1][1] = 1; ans.v[1][2] = 0;ans.v[2][0] = 0; ans.v[2][1] = 0; ans.v[2][2] = 1;while(k){if(k&1) ans = mul(ans,m);m = mul(m,m);k >>= 1;}return ans;
} int main(){scanf("%d",&t);while(t--){scanf("%lld%lld%lld%lld%lld%lld",&f1,&f2,&a,&b,&c,&k);if(k==1){printf("%lld\n",(f1+MOD)%MOD);}else if(k==2){printf("%lld\n",(f2+MOD)%MOD);}else{// 初始化要进行幂运算的矩阵 Matrix m1;m1.v[0][0] = b; m1.v[0][1] = a; m1.v[0][2] = 1;m1.v[1][0] = 1; m1.v[1][1] = 0; m1.v[1][2] = 0;m1.v[2][0] = 0; m1.v[2][1] = 0; m1.v[2][2] = 1;Matrix ans;ans = q_pow(m1,k-2);LL res = (ans.v[0][0]*f2+ans.v[0][1]*f1+ans.v[0][2]*c)%MOD;printf("%lld\n",(res+MOD)%MOD);}}return 0;
}