Description
相信大家都玩过“俄罗斯方块”游戏吧,“俄罗斯方块”是一个有趣的电脑小游戏,现有一个有C列、行不受限定游戏平台,每一次下落的方块是下列的7个图形的一种: 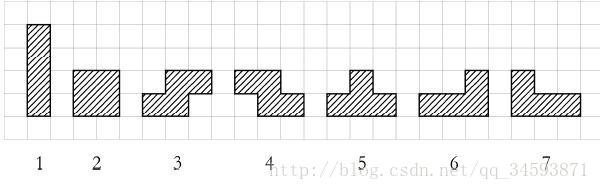
现给出每一列的初始高度和下落方块的形状,请你编写一个程序,求出落地的方法总数,也就是落地后,地表面形成的不同的形状总数。
Input
第一行为二个整数C和P,1 ≤ C ≤ 100, 1 ≤ P ≤ 7,表示列数和下落方块的编号 第二行共有用一个空隔隔开的C个整数,每一个数字在 0 到 100,之间(包含0和100),表示每一列的初始高度
Output
输出为一个整数,表示落地的方法总数
Sample Input
Input1
6 5
2 1 1 1 0 1
Input2
5 1
0 0 0 0 0
Input3
9 4
4 3 5 4 6 5 7 6 6
Sample Output
Output1
5
Output2
7
Output3
1
算法讨论
模拟
varn,m,i,j,k,l,sum:longint;a:array[1..500] of longint;
beginreadln(n,m);for i:=1 to n doread(a[i]);if m=1 thenbeginsum:=sum+n;for i:=1 to n-3 doif (a[i]=a[i+1])and(a[i]=a[i+2])and(a[i]=a[i+3]) theninc(sum);end;if m=2 thenfor i:=1 to n-1 doif a[i]=a[i+1] theninc(sum);if m=3 thenfor i:=1 to n-2 dobeginif (a[i]=a[i+1])and(a[i]+1=a[i+2]) theninc(sum);if a[i]-1=a[i+1] theninc(sum);end;if m=4 thenfor i:=1 to n-2 dobeginif (a[i+1]=a[i+2])and(a[i]-1=a[i+2]) theninc(sum);if a[i]+1=a[i+1] theninc(sum);end;if m=5 thenbeginfor i:=1 to n-2 doif (a[i]=a[i+1])and(a[i+1]=a[i+2])or(a[i]-1=a[i+1])and(a[i]=a[i+2]) theninc(sum);for i:=1 to n-1 doif (a[i]-1=a[i+1])or(a[i]+1=a[i+1]) theninc(sum);end;if m=6 thenbeginfor i:=1 to n-2 doif (a[i]=a[i+1])and(a[i]=a[i+2]) theninc(sum);for i:=1 to n-1 doif a[i]=a[i+1] then inc(sum);for i:=1 to n-1 doif a[i]=a[i+1]+2 then inc(sum);for i:=1 to n-2 doif (a[i+2]=a[i+1])and(a[i]=a[i+2]-1) then inc(sum);end;if m=7 thenbeginfor i:=1 to n-2 doif (a[i]=a[i+1])and(a[i]=a[i+2]) theninc(sum);for i:=1 to n-1 doif a[i]=a[i+1] then inc(sum);for i:=1 to n-1 doif a[i]=a[i+1]-2 then inc(sum);for i:=1 to n-2 doif (a[i]=a[i+1])and(a[i]=a[i+2]+1) then inc(sum);end;writeln(sum);
end.