【机器学习3】通过excel，python-矩阵求解法，python-sklearn 三种方法做重回归分析

1.Excel做重回归分析

1.直接把数据粘贴进去
(其中一列全为1，是为了方便用矩阵求偏回归系数)

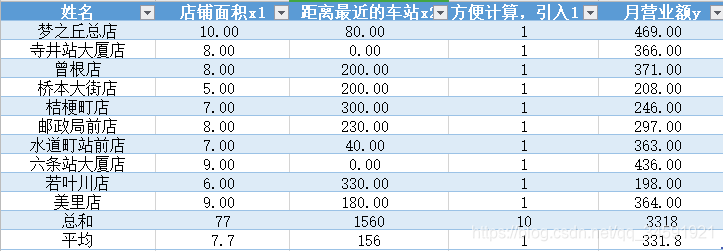
2.利用插入散点图工具画出散点图
(可以发现，两个变量都会影响到营业额)

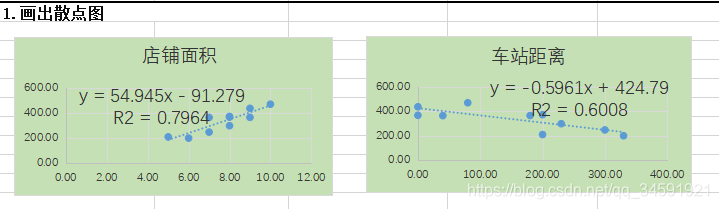
3.借助矩阵求偏回归系数

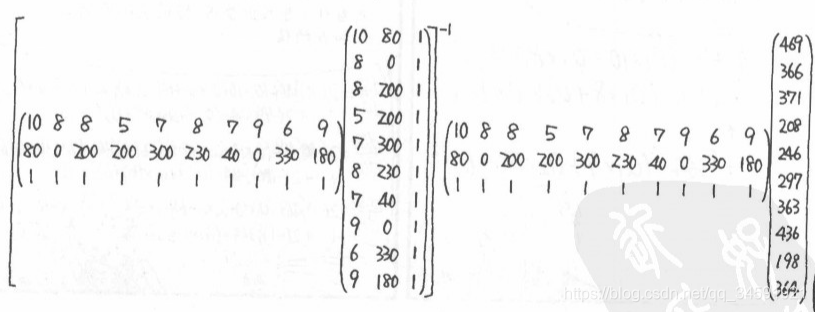
当然，这样复杂的计算我们交给excel去做，上图的矩阵乘法我们转化成excel里面的计算函数就是：

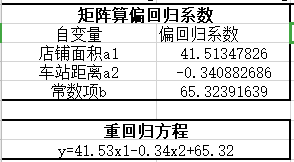
求出矩阵的偏回归系数，然后就可以书写出冲回归方程：

4.确认重回归方程的精度

当然，这里我们也可以用excel来算，把上面公式转换成excel计算函数就是：

直接得到R和R?：

2.python-矩阵求解法做重回归分析

直接上代码：

#利用线性代数的矩阵求解法求解多元线性回归方程的系数
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline
data = np.genfromtxt("/myjupyter\漫画数据1.csv",delimiter=",")
X1=data[1:11,1]#自变量温度
X2=data[1:11,2]#因变量销售量
Y=data[1:11,4]#自变量温度
#将因变量赋值给矩阵Y1
Y1=np.array([Y]).T
#为自变量系数矩阵X赋值
X11=np.array([X1]).T
X22=np.array([X2]).T
A=np.array([[1],[1],[1],[1],[1],[1],[1],[1],[1],[1]])#创建系数矩阵
B=np.hstack((A,X11))#将矩阵a与矩阵X11合并为矩阵b
X=np.hstack((B,X22))#将矩阵b与矩阵X22合并为矩阵X
#求矩阵X的转置矩阵
X_=X.T
#求矩阵X与他的转置矩阵的X_的乘积
X_X=np.dot(X_,X)
#求矩阵X与他的转置矩阵的X_的乘积的逆矩阵
X_X_=np.linalg.inv(X_X)
#求解系数矩阵W，分别对应截距b、a1、和a2
W=np.dot(np.dot((X_X_),(X_)),Y1)
b=W[0][0]
a1=W[1][0]
a2=W[2][0]
print("系数a1=",a1)
print("系数a2=",a2)
print("截距为=",b)
print("多元线性回归方程为:y=",a1,"X1+",a2,"X2+",b)
#画出线性回归分析图
data1=pd.read_excel('/myjupyter\漫画数据1.xls')
sns.pairplot(data1, x_vars=['areax1','disx2'], y_vars='gety', height=3, aspect=0.8, kind='reg')  
plt.show() 
#求月销售量Y的和以及平均值y1
sumy=0#因变量的和
y1=0#因变量的平均值
for i in range(0,len(Y)):sumy=sumy+Y[i]
y1=sumy/len(Y)
#求月销售额y-他的平均值的和
y_y1=0#y-y1的值的和
for i in range(0,len(Y)):y_y1=y_y1+(Y[i]-y1)
print("销售量-销售量平均值的和为:",y_y1)
#求预测值sales1
sales1=[]
for i in range(0,len(Y)):sales1.append(a1*X1[i]+a2*X2[i]+b)
#求预测值的平均值y2
y2=0
sumy2=0
for i in range(len(sales1)):sumy2=sumy2+sales1[i]
y2=sumy2/len(sales1)
#求预测值-平均值的和y11_y2
y11_y2=0
for i in range(0,len(sales1)):y11_y2=y11_y2+(sales1[i]-y2)
print("预测销售值-预测销售平均值的和为:",y11_y2)
#求月销售额y-他的平均值的平方和
Syy=0#y-y1的值的平方和
for i in range(0,len(Y)):Syy=Syy+((Y[i]-y1)*(Y[i]-y1))
print("Syy=",Syy)
#求y1-y1平均的平方和
Sy1y1=0
for i in range(0,len(sales1)):Sy1y1=Sy1y1+((sales1[i]-y2)*(sales1[i]-y2))
print("Sy1y1=",Sy1y1)
#（y1-y1平均）*（y-y平均）
Syy1=0
for i in range(0,len(sales1)):Syy1=Syy1+((Y[i]-y1)*(sales1[i]-y2))
print("Syy1=",Syy1)
#求R
R=Syy1/((Syy*Sy1y1)**0.5)
R2=R*R
print("判定系数R2=",R2)

结果如图：

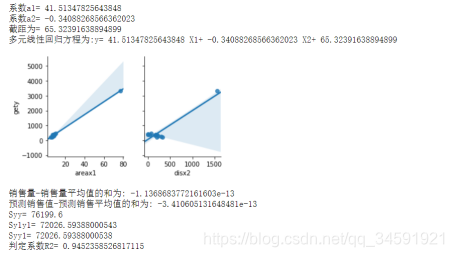
3.python借助sklearn做重回归分析

直接上代码：

import pandas as pd
import seaborn as sns  
import matplotlib.pyplot as plt
from sklearn import linear_model
%matplotlib inline
data=pd.read_excel('/myjupyter\漫画数据1.xls')
#print(data.head())
#print(data.tail()) 
X=data[['areax1','disx2']]   
y=data['gety']    
y=data.gety   
model = linear_model.LinearRegression()
model.fit(X,y)
print("X1=",model.coef_[0])
print("X2=",model.coef_[1])
print("截距为=",model.intercept_)
print("多元线性回归方程为:y=",model.coef_[0],"X1+",model.coef_[1],"X2+",model.intercept_)
sns.pairplot(data, x_vars=['areax1','disx2'], y_vars='gety', height=3, aspect=0.8, kind='reg')  
plt.show()  

结果如图：

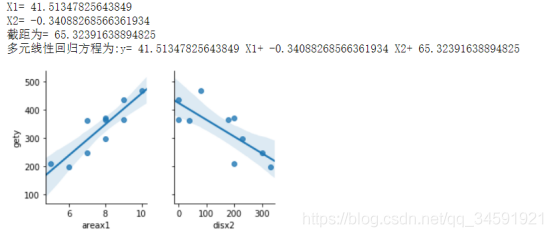
4.三种结果对比

①Excel

y=41.53x1-0.34x2+65.32
R?=0.945235213

②自行推断

y=41.51X1-0.34X2+ 65.32
R2= 0.94523585

③借助sklearn

y= 41.51X1-0.34X2+ 65.32

参考链接：https://blog.csdn.net/qq_42451251/article/details/105019128
参考链接：https://blog.csdn.net/qq_42451251/article/details/104974718