目录
1、算法性能
2、选择排序
2.1、描述
2.2、特点
2.3、代码实现
3、插入排序
3.1、描述
3.2、特点
3.3、代码实现
4、插入排序的优化
4.1、优化方案
4.2、输出结果
1、算法性能
评估一个算法的性能我们首先计算该算法执行语句的次数(包括比较、交换、读写数组的次数),同样我们还需要考虑算法的内存开销,排序算法一般分为两类:除了函数调用所需的栈和固定数目的实例变量之外无需额外内存的原地排序算法,以及需要额外内存空间来存储另 一份数组副本的其他排序算法。
2、选择排序
2.1、描述
在长度为N的无序数组中,第一次遍历n-1个数,找到最小的数值与第一个元素交换;
第二次遍历n-2个数,找到最小的数值与第二个元素交换;
。。。
第n-1次遍历,找到最小的数值与第n-1个元素交换,排序完成。
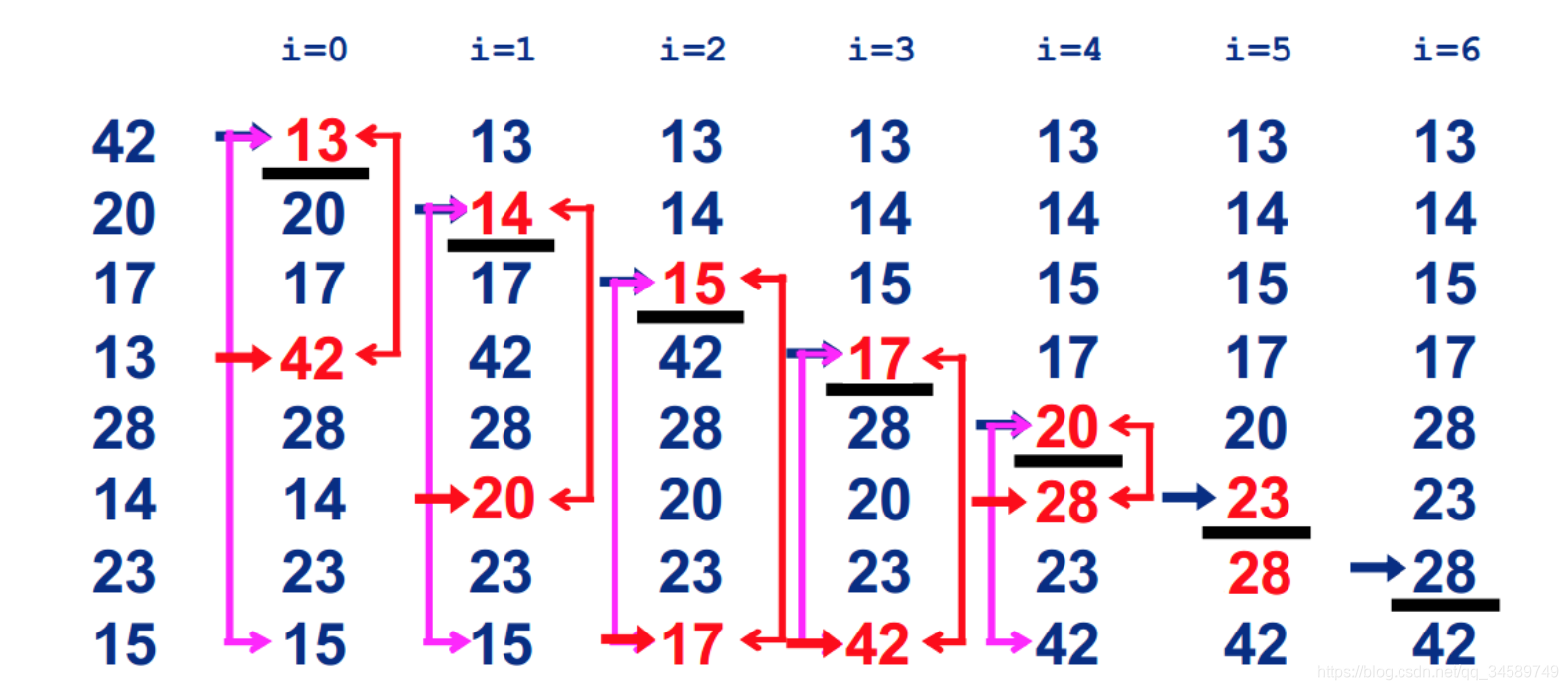
2.2、特点
- 时间复杂度为O(N^2) ~(N-1)+(N-2)+...+2+1=N(N-1)/2 ~ N^2/2
- 运行时间和输入无关(不管输入的是有序或者无序的,排序所需时间相同)
- 数据移动是最少的.(用了N次交换数据)----------------------------------------------------------------------------------------------------------------优势
2.3、代码实现
public class Selection {public static int[] sort(int[] a) {int min;for (int i = 0; i < a.length; i++) {min = i;for (int j = i+1; j < a.length; j++) {if (a[min] > a[j]) {min = j;}}exch(a, i, min);}return a;}private static void exch(int[] a, int i, int j) {int temp = a[i];a[i] = a[j];a[j] = temp;}public static void show(int[] a) {for (int item:a){System.out.print(item+",");}}public static void main(String[] args) {int[] a= {1,3,2,11,22,33,44,55,22,12,11,13,12,15,45,7,8,68,56,43,55,78};int[] result=sort(a);show(result);}
}3、插入排序
3.1、描述
在要排序的一组数中,假定前n-1个数已经排好序,现在将第n个数插到前面的有序数列中,使得这n个数也是排好顺序的。如此反复循环,直到全部排好顺序。
通俗说就是,{1,3,5,2,7,0.....} 假定 1,3,5是排序好的,我们通过将2和这三个数比较,2比5小,和我换一下位置,比3小再换一下位置,直到换到合适的位置。
算法实现里边,我们假定j-1个元素是排序好的,每次拿数组里边的第j(j=i)个元素和j以前的所有元素比较,交换位置,直到换到自己该待的位置。
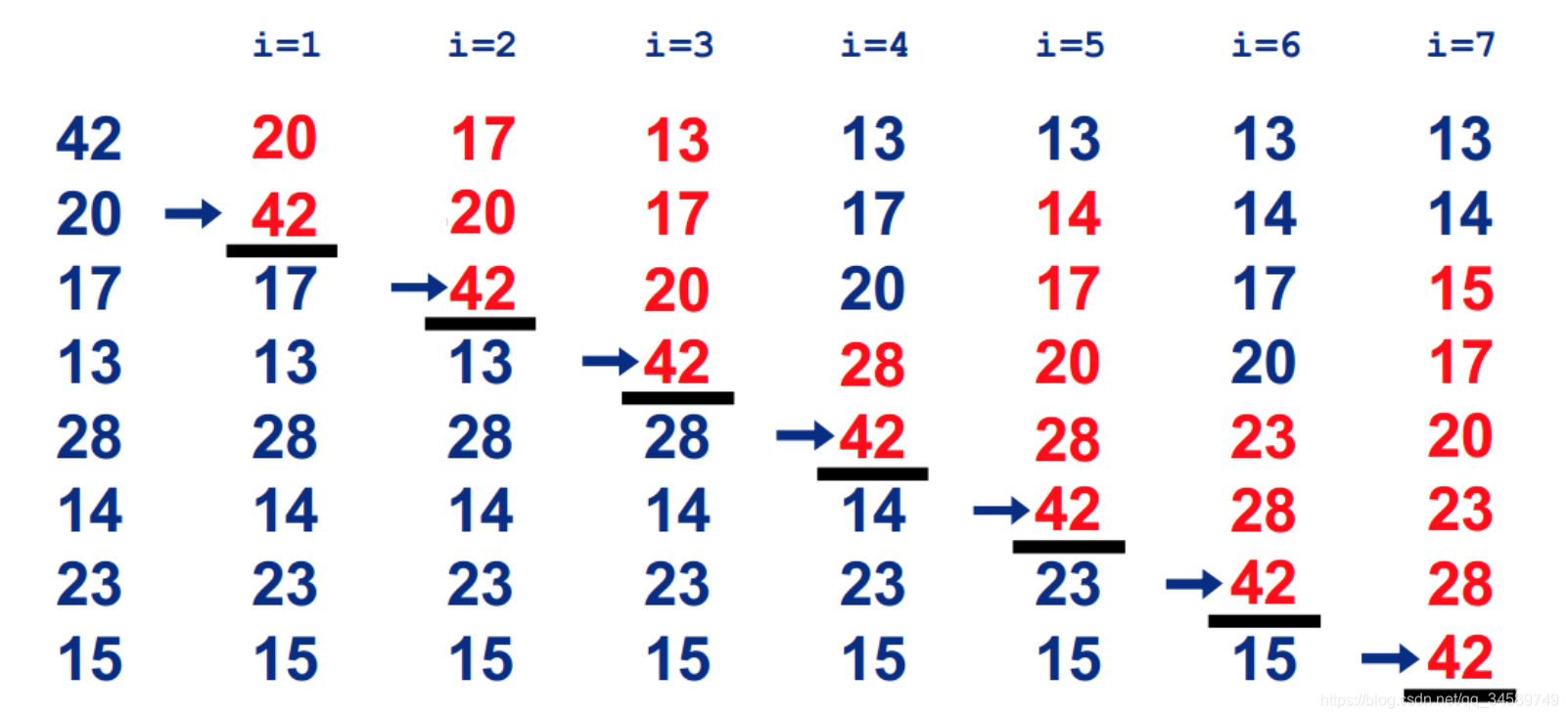
3.2、特点
- 时间复杂度为O(N^2)
- 运行时间与输入数组的初始顺序有关。(对于一些部分有序的数组,该算法有很大的--------------------------------------------优势)
对于随机排列的长度为 N 且主键不重复的数组,平均情况下插入排序需要~ N^2/4 次比 较以及~ N^2/4 次交换。最坏情况下需要~ N^2/2 次比较和~ N^2/2 次交换,最好情况下需要 N-1 次比较和 0 次交换。
倒置:是指数组中两个顺序掉到的元素。比如{1,5,3,2} 中的倒置有三对:5-3、5-2、3-2。
插入排序中需要交换元素的次数和倒置的对数是一样的。需要的比较次数大于等于倒置的 数量,小于等于倒置的数量加上数组的大小再减一。
3.3、代码实现
public class Insertion {private static int[] sort(int[] a) {for (int i = 1; i < a.length; i++) {for (int j = i; j >0; j--) {if (a[j] < a[j-1]) {exch(a,j,j-1);}else {break;}}}return a;}private static void exch(int[] a, int i, int j) {int temp = a[i];a[i] = a[j];a[j] = temp;}private static void show(int[] a) {for (int item:a){System.out.print(item+",");}}public static void main(String[] args) {int[] a= {1,3,2,11,22,33,44,55,22,12,11,13,12,15,45,7,8,68,56,43,55,78};int[] result=sort(a);show(result);}
}
4、插入排序的优化
4.1、优化方案
原始方案:{1,3,5,2,7,0.....} 假定 1,3,5是排序好的,我们通过将2和这三个数比较,2比5小,和我换一下位置,比3小再换一下位置,直到换到合适的位置。
优化方案X:{1,3,5,2,7,0.....} 假定1,3,5还是排序好的,我们通过将2和这三个数比较,如果2比5小,5后移到2的位置,2比3小,3后移到原来5的位置,最后,3的位置就空给2 了,最后再把2赋值到3原来的位置上。
优化方案Y:{1,3,5,2,7,0.....} 先把遍历一边数组,把最小的元素0一道第一的位置,得到的数组{0,1,3,5,2,7,.....} ,然后再在这个基础上进行原始方案的排序。
public class Insertion {static int count = 0;static int countX = 0;static int countY = 0;private static void sort(int[] a) {for (int i = 1; i < a.length; i++) {for (int j = i; j > 0; j--) {if (a[j] < a[j - 1]) {count++;exch(a, j, j - 1);} else {break;}}show(a);}}private static void sortX(int[] a) {int N = a.length;for (int i = 1; i < N; i++) {int temp = a[i];int j = i;for (; j > 0; j--) {if (temp < a[j - 1]) {countX++;a[j] = a[j - 1];} else {break;}}a[j] = temp;show(a);}}public static void sortY(int[] a) {int N = a.length;boolean isExchanged = false;for (int i = N - 1; i > 0; i--) {if (a[i]<a[i - 1]) {exch(a, i, i - 1);countY++;isExchanged = true;}}show(a);if (!isExchanged) {return;}for (int i = 2; i < N; i++) {for (int j = i; a[j]<a[j - 1]; j--) {exch(a, j, j - 1);countY++;}show(a);}}private static void exch(int[] a, int i, int j) {int temp = a[i];a[i] = a[j];a[j] = temp;}private static void show(int[] a) {System.out.println("\n");for (int item : a) {System.out.print(item + ",");}}public static void main(String[] args) {int[] a = { 6,4,2,3,1,9,8,7};show(a);sort(a);System.out.println("\n-------------------------");int[] b = { 6,4,2,3,1,9,8,7};show(b);sortX(b);System.out.println("\n-------------------------");int[] c = { 6,4,2,3,1,9,8,7};show(c);sortY(c);System.out.println("\n-------------------------");System.out.println("\ncount=" + count);System.out.println("\ncountX=" + countX);System.out.println("\ncountY=" + countY);}}4.2、输出结果
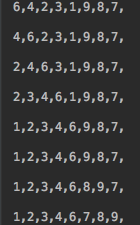
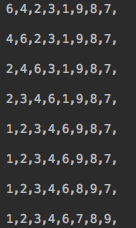
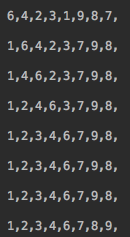
sort sortX sortY
前面两种数据的变化是一样的,最后一种的变化只是先将1移到了第一的位置,其余的是一样的,对这三种方法进行万级的数组测试的话,sortX能比sort快1.7倍左右,sortY比sort快1.5倍作用。变化不是很大, 他们的时间复杂度都是O(N^2)。
本文内容部分来之于《算法》和菜鸟教程,本文主要目的是自己的学习笔记和技术分享。