【Codejam2008_Round1C】C:Increasing Speed Limits

题目大意：

给出一个长度为n(n<=500000)数字串a，求这个串中严格递增的序列个数，序列长度可为1

分析：

什么鬼！上升序列？？相比做的前两场的C题，这次的C题在题目类型上就比较温和了，毕竟是很熟悉的DP模型。不难想到，设$dp[i]$为以i为末尾的严格上升序列的个数。
转移就很容易想到了，

$$dp[i]=\sum_{j=1}^{i-1}dp[j](a[j]<a[i])$$

这样的复杂度很显然是$O(n^2)$，不炸完才怪咧
这种情况下，暂时不要放弃DP，考虑考虑优化是比较合理的。（当然，对于这道题似乎不用DP也有其他做法）
状态已经是一维，再压缩已不现实，考虑转移优化。
观察转移式，区间求和。。。赤裸裸地告诉你是线段树优化。
然而这个转移式还是有条件的，要求$a[j]<a[i]$，判定条件对数据结构是不友好的（因为要你根据条件手动改写数据结构），但对于这种比较基础的判定条件，还是可以做的。
不难想到根据a的值排一次序，在线段树中按照排序后的顺序存储（可能在a中多个位置对应线段树中同一个值）

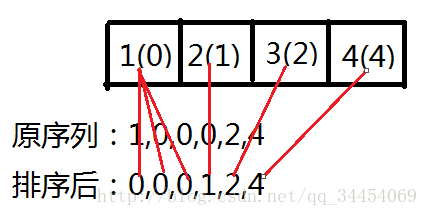
设a序列中每个位置对应的线段树中的位置为b[i]
线段树中每个区间存储一个区间和。每次转移就可以直接从1-b[i]-1求一个区间和就可以了，我们从前往后依次枚举，转移完就把当前位置的dp值更改到线段树中，这样做就不用担心把i之后的dp值选用了。
注：代码被学校的增霸卡刷掉了。。。正在补中。。。