【枚举】hihocoder1646 Rikka with String II

描述

众所周知，萌萌哒六花不擅长数学，所以勇太给了她一些数学问题做练习，其中有一道是这样的：

对于 n 个 01 字符串 si，定义他们的权值是这 n个 si 的串插入一个空的 Trie 树后得到的结果 Trie 中的节点个数。例如 [“01”,”00”] 的权值是4，[“010”,”1”] 的权值是5。

现在勇太给出了 n 个只包含 01? 的字符串 si。其中 ? 表示既有可能是 0 也有可能是 1。显然，如果有 K 个 ?，那么一共有 2K 个可能的字符串集合。

现在勇太想要知道对于这 2K 种状态，权值的和是多少。

当然，这个问题对于萌萌哒六花来说实在是太难了，你可以帮帮她吗？

分析

对于每一种方案而言，其节点总数其实就是所有不重复的公共前缀数。
这里需要用的容斥原理：
即

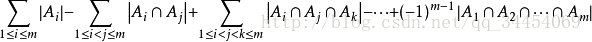
具体的证明在baidu上还是比较清晰的

因为最多只有20个数列，所以我们可以暴力枚举其中的一个子集，再$O（|S|）$的复杂度来求出当前子集在所有方案中的前缀总数，设这个值为$f(S)$

那么答案就是

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
#define SF scanf
#define PF printf
#define MOD 998244353
#define MAXN 25
#define MAXL 55
using namespace std;
int n,tot,sum;
char s[MAXN][MAXL];
long long slen,ans1,pw[MAXN*MAXL];
vector<int> a;
int main(){SF("%d",&n);for(int i=0;i<n;i++){SF("%s",s[i]);int len=strlen(s[i]);slen+=len;}for(int i=0;i<n;i++){int len=strlen(s[i]);for(int j=0;j<len;j++)if(s[i][j]=='?')tot++;}pw[0]=1;for(int i=1;i<=tot;i++)pw[i]=(pw[i-1]<<1ll)%MOD;slen=(pw[tot]*slen)%MOD;for(int s1=1;s1<(1<<n);s1++){int len=MAXL,pre=0;sum=tot;long long ans=0;a.clear();for(int i=0;i<n;i++)if(s1&(1<<i))a.push_back(i);for(int i=0;i<a.size();i++){int len1=strlen(s[a[i]]);len=min(len1,len);}int j;for(j=0;j<len;j++){int flag=-1;int nowl=0;for(int i=0;i<a.size();i++)if(s[a[i]][j]=='?'){nowl++;}else if(s[a[i]][j]=='0'){if(flag==1){flag=2;break;}elseflag=0;}else if(s[a[i]][j]=='1'){if(flag==0){flag=2;break;}elseflag=1;}sum-=nowl;if(flag==2){break;}else if(flag==-1){pre++;}ans=(ans+pw[pre+sum])%MOD;}if(a.size()%2==1)ans1=(ans1+ans)%MOD;elseans1=(ans1+MOD-ans)%MOD;}PF("%lld",(ans1+pw[tot])%MOD);}

说来也惭愧。。可能是当时因为感冒发烧，脑子不好使，这么简单一道水题居然看了半天。。题解都看了好久才看懂。。。OIers一定要注意身体啊。。