【数据结构】【线段树并查集栈】CF500E New Year Domino

题意：

给出N个多米诺骨牌（均位于一条数轴上），每个骨牌有一个高度与坐标，现在有Q次询问，
每次询问给出$L与R$,现在推倒第$L$个骨牌，我们可以给某些骨牌临时增加高度（仅用于此次询问），每增加1高度，需要1的代价，现在要使第$R$个骨牌倒下，求最小的代价。

分析：

首先，我们有一个直观的想法：我们将每个骨牌延长，使得它倒下后能碰到它后面一个骨牌。
然而，有一种情况，使得这个算法失败：

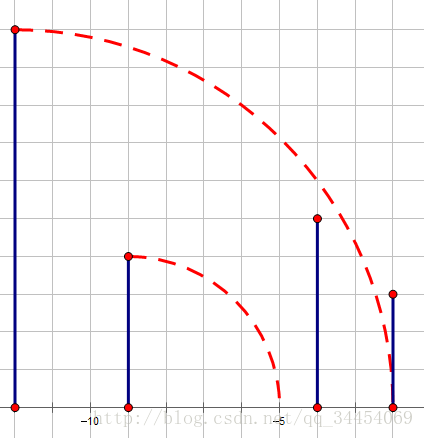
靠前的一个骨牌可能会相当的长，以至于它倒下后，能够超过它后面的一个骨牌倒下后达到的最远距离。这样如果询问包括了这个靠前的骨牌，那么中间那个骨牌就没必要延长了。

所以我们试图排除之前的骨牌对后面骨牌的影响：
离线操作，将询问按照L从大到小排序，同时从后往前插入骨牌，一直插入到L为止。
然后询问的时候，就不需要考虑未插入骨牌，对已插入骨牌的影响。

现在的目标是，如何插入一个骨牌？

我们将问题转化一下，如果我们把每个骨牌看作一个点，要求如果一个骨牌倒下，那么它能够压倒的骨牌与它在同一个联通块。这样一来，我们可以把问题转化成如下形式：

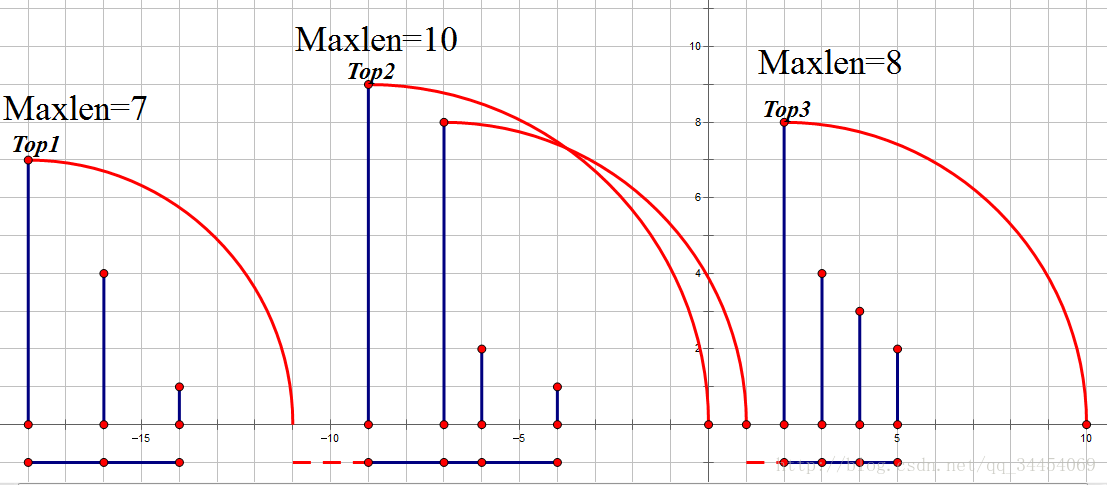
同一个联通块内部，当第一个倒下后，全部都不需要任何代价可以倒下，我们处理询问时，只需要计算不同联通块之间的代价即可。

我们现在来看插入一个骨牌的具体操作：

假设我们现在要插入F：
首先，我们用栈来存储每个联通块的第一个位置：
现在我们的栈内的元素是：
G,H

首先，求出F倒下后能够到达的位置，我们从栈顶依次判断：
G的位置在F倒下的范围内，G加入F的联通块（用并查集维护），$val_G$改为0
更新当前联通块能够到达的最远距离：
因为：$Lenmax(F)<Lenmax(G)$,所以$Lenmax(F)=Lenmax(G)$
栈中弹出G
H的位置不在F倒下的范围内，H不加入联通快。
将F压如栈，$val_F$为$Pos(H)-Lenmax(F)-Pos(F)=1$
同时，将$val_{F+1}...val_G$都修改为0
这样，我们就完成了一次插入

询问时，我们求出$\sum_{i=l}^{i<=fa[r]-1}val_i$即可（fa[r]表示r所在的并查集的根）
所以我们需要线段树来存储val数组。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<stack>
#define SF scanf
#define PF printf
#define MAXN 200010
using namespace std;
int blo[MAXN],n,m,x,y;
long long tree[MAXN*4],tag[MAXN*4],p[MAXN],l[MAXN],ans[MAXN];
struct node{int l,r,id;
}q[MAXN];
stack<int> s;
int fa[MAXN];
int get_fa(int x){if(fa[x]==0)return x;fa[x]=get_fa(fa[x]);return fa[x];
}
void Add(int l,int r,int id,int x,int val,bool flag){if(l==r){tree[id]+=val;if(flag==1)tree[id]=0;return ;}int mid=(l+r)>>1;if(x<=mid)Add(l,mid,id*2,x,val,flag);elseAdd(mid+1,r,id*2+1,x,val,flag);tree[id]=tree[id*2]+tree[id*2+1];
}
long long Query(int l,int r,int id,int l1,int r1){if(l1<=l&&r<=r1)return tree[id];int mid=(l+r)>>1;long long res=0;if(l1<=mid)res+=Query(l,mid,id*2,l1,r1);if(r1>mid)res+=Query(mid+1,r,id*2+1,l1,r1);return res;
}
void Add(int x){long long maxl=0;while(!s.empty()&&p[s.top()]<=l[x]){maxl=max(l[s.top()],maxl);fa[s.top()]=x;Add(1,n,1,s.top(),0,1);s.pop();}l[x]=max(l[x],maxl);if(!s.empty())Add(1,n,1,x,max(0ll,p[s.top()]-l[x]),0);s.push(x);
}
bool cmp(node a,node b){if(a.l!=b.l)return a.l>b.l;return a.r<b.r;
}
int main(){SF("%d",&n);for(int i=1;i<=n;i++){SF("%I64d%I64d",&p[i],&l[i]);l[i]+=p[i];}SF("%d",&m);for(int i=1;i<=m;i++){SF("%d%d",&q[i].l,&q[i].r);q[i].id=i;}sort(q+1,q+1+m,cmp);int now=n;for(int i=1;i<=m;i++){while(now>=q[i].l)Add(now--);if(now<get_fa(q[i].r)-1)ans[q[i].id]=Query(1,n,1,now+1,get_fa(q[i].r)-1);}for(int i=1;i<=m;i++)PF("%I64d\n",ans[i]);
}