【数论】【图论】【Exgcd】【LCA】Codeforces500G

题意：

给出一棵树，有m组询问，每组询问包含2对点(u,v)和(x,y)。现在一个人从u出发，在u和v之间的路径上来回移动，一个人从x出发，在x和y上的路径来回移动，求什么时候两人能刚好出现在一个点上。如果不能输出-1

分析

非常棒的一道题啊。。。

首先，要把这个在图上的问题转化成数论问题：

对于每次询问，我们找到以下信息：
两条路径各自的长度，相交部分的长度，相交部分的两个端点。

当然，这一堆看似复杂的东西都可以简单地利用lca求出

首先求出这两对点的lca中，深度较大的一个，设为p，如果存在相交部分，那一定是p的子节点。这应该比较显然。因为在路径(u,v)上的点一定是lca(u,v)的子节点，对(x,y)同理，因为公共部分既在(u,v)上，又在(x,y)上，所以一定两个都得满足。

现在反过来，求在路径(u,v)上但不在(x,y)上的点，其必然是路径(u,x)与(u,y)的相交部分。以及(v,x)与(v,y)的相交部分。

所以：
求lca(u,x)，lca(u,y)中深度较大的一个，设为a。
求lca(v,x)，lca(v,y)中深度较大的一个，设为b。

我们要求的相交部分，就是从a和b向上走，直到p之前的点。

现在问题转化为：

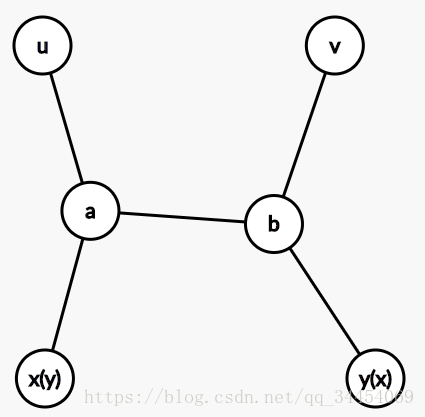
一个人在u,v之间来回鬼畜，一个人在x,y之间来回鬼畜。

求第一次相遇的时间。

分为两种情况讨论：
相遇时是从同一个方向，不同的方向。
同一个方向比较容易，设最终是经过x步到达，那么满足条件：
$dist(u,a)+A*dist(u,v)=dist(x,a)+B*dist(x,y)$
移一下项，就变成exgcd的问题了。

不同的方向比较麻烦，因为满足的不再是等式了

它变为求
$dist(u,a)+A*dist(u,v)+T=dist(a,b)-T+dist(x,b)+B*dist(x,y)(T\leq dist(a,b))$
这个T变量的存在使得无法使用exgcd。

这里官方题解讲得很清楚，我就不再写了
http://codeforces.com/blog/entry/15488

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
#define SF scanf
#define PF printf
#define MAXN 200010
#define INF 100000000000000000ll
using namespace std;
typedef long long ll;
int fa[MAXN][20],dep[MAXN];
vector<int> a[MAXN];
int n,q;
void dfs(int x,int f){fa[x][0]=f;dep[x]=dep[f]+1;for(int i=0;i<a[x].size();i++){int u=a[x][i];if(u==f)continue;dfs(u,x);   }
}
int lca(int u,int v){if(dep[u]<dep[v])swap(u,v);for(int i=19;i>=0;i--)if(dep[fa[u][i]]>=dep[v])u=fa[u][i];if(u==v)return u;for(int i=19;i>=0;i--)if(fa[u][i]!=fa[v][i]){u=fa[u][i];v=fa[v][i];}return fa[u][0];
}
int lower(int x,int y){if(dep[x]<dep[y])return y;return x;
}
int dist(int x,int y){int l=lca(x,y);return dep[x]+dep[y]-2*dep[l];  
}
int gcd(int x,int y){if(y==0)return x;return gcd(y,x%y);  
}
ll exgcd(ll x,ll y,ll g){if(g==0)return 0;ll t=exgcd(y%x,x,g%x);t=(g-t*y)/x;if(t<0){t+=(-t)/y*y;t+=y;}return t%y;
}
ll Samedir(ll t1,ll d1,ll t2,ll d2,ll l){ll g=(gcd(t1,t2)),m=d2-d1;ll tt=t1;if(m<0)m+=t2;if(m%g)return INF;t1/=g,m/=g,t2/=g;return exgcd(t1,t2,m)*tt+d1;
}
ll G(ll x,ll y,ll l,ll r){x%=y;if(x*2>y)   return G(y-x,y,y-r,y-l);ll t=l/x,rest=y%x;ll a,b;if(l==t*x)return t;if((t+1ll)*x<=r)return t+1ll;a=G(x-rest,x,l%x,r%x);a=(a*y-1ll)/x+1ll;b=a*x%y;a+=(r-b)/x;return a;
}
ll D(ll x,ll y,ll l,ll r){ll res=INF,g=gcd(x,y);if(l==0){res=y/g;l=1;}if((l-1)/g>=r/g)return INF;return min(res,G(x,y,l,r));
}
ll Diffdir(ll t1,ll d1,ll t2,ll d2,ll l){ll bg=d2-d1-l,ed=d2-d1+l;   ll p;if(bg<0)bg+=(-bg)/t2*t2;if(ed<0)ed+=(-ed)/t2*t2;bg=(bg+t2)%t2;ed=(ed+t2)%t2;if(ed%2ll)return INF;if(t2==l*2){return d1+ed/2ll;}if(bg>ed||bg==0)return d1+ed/2ll;p=D(t1,t2,bg,ed);if(p==INF)return INF;return t1*p+d1+l-(p*t1%t2-bg)/2ll;
}
ll Query(int u,int v,int x,int y){int p1=lca(u,v),p2=lca(x,y);int p3=lca(u,x),p4=lca(v,x);int p5=lca(u,y),p6=lca(v,y);int p,a,b;p=lower(p1,p2);a=lower(p3,p5);b=lower(p4,p6);if(dep[a]<dep[p]&&dep[b]<dep[p])return -1;if(dep[a]<dep[p])a=p;if(dep[b]<dep[p])b=p;int d1=dist(u,v)*2,d4=dist(x,y)*2;int d2=dist(u,a),d3=dist(u,b);int d5=dist(x,a),d6=dist(x,b);int d=dist(a,b);if(d2<=d3)d3=d1-d3;elsed2=d1-d2;if(d5<=d6)d6=d4-d6;elsed5=d4-d5;return min(min(Samedir(d1,d2,d4,d5,d),Samedir(d1,d3,d4,d6,d)),min(Diffdir(d1,d2,d4,d6,d),Diffdir(d1,d3,d4,d5,d)));
}
int main(){SF("%d",&n);int u,v;for(int i=1;i<n;i++){SF("%d%d",&u,&v);a[u].push_back(v);a[v].push_back(u);}dfs(1,0);for(int j=1;j<20;j++)for(int i=1;i<=n;i++)fa[i][j]=fa[fa[i][j-1]][j-1];SF("%d",&q);int x,y;for(int i=1;i<=q;i++){SF("%d%d%d%d",&u,&v,&x,&y);ll res=Query(u,v,x,y);if(res==INF)PF("-1\n");elsePF("%I64d\n",Query(u,v,x,y));}
}