题意:
给出N个数,两人依次选择一种操作:
1、删去最大的一个数
2、所有数-1
不能走的算获胜,求谁必胜。
分析:
有趣。。。这题真心有趣。。。
首先,把这N个数从大到小排序,画成一个图:
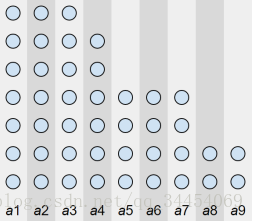
每种操作就相当于:删去最左边一列,或删去最下面一行。
然后观察剩余部分的左下角坐标:发现它是从(0,0)出发,每次向上走(删去最下面一行),向右走(删去最左边一列),最终到达边界的一条路径。

所以就可以把每个点存一个NP状态。
边界的都为必胜,然后按照NP状态的定义进行转移。
但就这么转移肯定会T
然后可以把NP状态画一下,发现:每一个斜对角线(除去边界)NP状态都是一样的
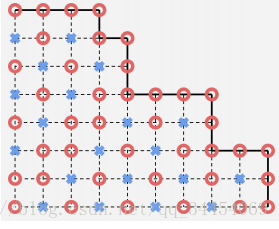
证明很简单:
如果点(x,y)是必胜,那么(x+1,y)或(x,y+1)是必败,但无论谁是哪个必败,都必须使(x+1,y+1)必胜,因为(x+1,y)可以向右走到达(x+1,y+1),(x,y+1)可以向上走到达(x+1,y+1)。
如果点(x,y)是必败,那么(x+1,y)与(x,y+1)都为必胜,根据上面所证明的,则(x+2,y+1),(x+1,y+2)均为必胜,那么(x+1,y+1)则为必败。
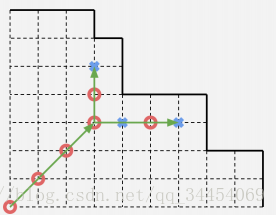
所以就可以直接根据(0,0)所在的斜对角线,求出其对应的未到达边界的最高的一个点,然后从那个点出发,观察其上方还剩多少个点,右方还剩多少个点,当且仅当两者均为奇数时,答案为必败,否则为必胜
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#define SF scanf
#define PF printf
#define MAXN 100010
using namespace std;
int a[MAXN];
bool cmp(int x,int y){return x>y;
}
int main(){int n,m,q;SF("%d",&n);for(int i=1;i<=n;i++)SF("%d",&a[i]);sort(a+1,a+1+n,cmp);a[0]=a[1];for(int i=0;;i++)if(i+2>a[i+2]){int x=i;int len1=a[i+1]-x;int len2=1;for(;a[i+len2+1]>x;len2++);if(len1%2==1&&len2%2==1)PF("Second");elsePF("First");break;}
}