【枚举】AGC030 B Tree Burning

题意：

给出一个环，从0位置出发，每次顺时针/逆时针走，直到第一个被标记的点，然后消除其标记，再选一个方向继续走。求消去所有标记后，能走的最长长度。

分析：

听说这题把TLY大佬卡住了。。。

估计他睡着了？

这题其实还是挺水的。

很显然，可以枚举最终停在哪个位置。然后，之前走的方式一定是来回鬼畜：

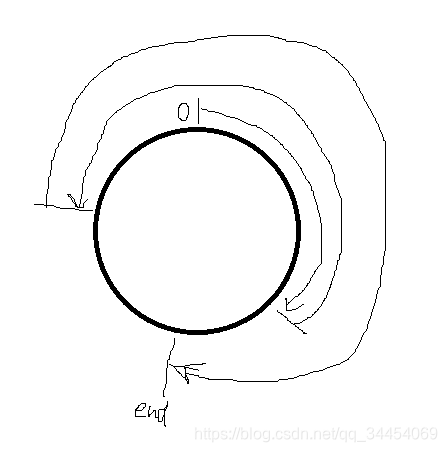
很显然，设$num=min(n?i,i?1)$，那么在两侧各会鬼畜num次，而最后一步的方向若是顺时针，则逆时针左边可以多鬼畜一次；最后一步是逆时针，则右边可以多鬼畜一次。

然后就直接沿顺时针/逆时针方向，暴枚任意一个点作为结束点即可。

#include<cstdio>
#include<cstring>
#include<cmath>
#include<vector>
#define SF scanf
#define PF printf
#define MAXN 200010
using namespace std;
typedef long long ll;
int n;
ll ans,a[MAXN],L,lft,rit,nstl,nstr,num;
int main(){
    SF("%lld%d",&L,&n);for(int i=1;i<=n;i++)SF("%lld",&a[i]);ans=a[n];nstl=n;nstr=n+1;for(int i=n;i>=1;i--){
    //block between i and i-1num=min(n-i,i-1);rit-=a[i];while(i-nstr<num&&nstr>1){
    nstr--;rit+=(a[nstr]);	}while(nstl-i>num&&nstl>0){
    lft-=(L-a[nstl]);nstl--;}
// PF("[%d %lld %lld %lld]\n",i,lft,rit,(lft+rit)*2+max(L-a[i],a[i]));int lastl,lastr;if(nstl==n)lastl=0;elselastl=(L-a[nstl+1])*2;if(nstr==0)lastr=0;elselastr=a[nstr-1]*2;ans=max(ans,(lft+rit)*2+max(a[i]+lastl,L-a[i]+lastr));lft+=(L-a[i]);}PF("%lld",ans);
}