KNN算法说明以及sklearn 中 neighbors.KNeighborsClassifier参数说明_综合

文章目录

:rose:KNN
:rose: sklearn 中 neighbors.KNeighborsClassifier参数说明

?KNN

概念

k-近邻算法（k-Nearest Neighbour algorithm），又称为KNN算法，是数据挖掘技术中原理最简单的算法。KNN的工作原理：给定一个已知标签类别的训练数据集，输入没有标签的新数据后，在训练数据集中找到与新数据最邻近的k个实例，如果这k个实例的多数属于某个类别，那么新数据就属于这个类别。可以简单理解为：由那些离X最近的k个点来投票决定X归为哪一类。

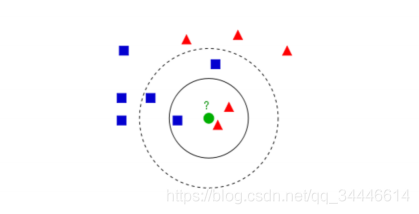
有红色三角和蓝色方块两种类别，我们现在需要判断绿色圆点属于哪种类别
当k=3时，绿色圆点属于红色三角这种类别；
当k=5时，绿色圆点属于蓝色方块这种类别。
k-近邻算法步骤

(1) 计算已知类别数据集中的点与当前点之间的距离；
(2) 按照距离递增次序排序；
(3) 选取与当前点距离最小的k个点；
(4) 确定前k个点所在类别的出现频率；
(5) 返回前k个点出现频率最高的类别作为当前点的预测类别。

KNN的工作原理

存在一个训练样本集合A，在给定测试样本b时，基于某种距离度量，找出训练集A中与测试样本b最靠近的k个训练样本（通常k≤20且为整数），之后，基于这k个训练样本的信息来预测种类或值。
其中，在分类问题中，KNN用来预测种类。一般使用“投票法”，选择这k个样本中出现最多的类别来作为测试样本的类别。
在回归问题中，KNN预测一个值。使用“平均法”，将k个样本的实值输出的平均值作为测试样本的输出。

一般情况下，距离度量选择欧式距离。距离公式：

二维
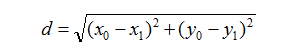
三维

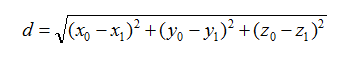
多维类推…

优缺点
- 优点
  
  简单好用，容易理解，精度高，理论成熟，既可以用来做分类也可以用来做回归
  可用于数值型数据和离散型数据
  无数据输入假定
  适合对稀有事件进行分类
- 缺点
  
  计算复杂性高；空间复杂性高；
  计算量太大，所以一般数值很大的时候不用这个，但是单个样本又不能太少，否则容易发生误分
  样本不平衡问题（即有些类别的样本数量很多，而其它样本的数量很少）
  可理解性比较差，无法给出数据的内在含义

? sklearn 中 neighbors.KNeighborsClassifier参数说明

KNeighborsClassifier(n_neighbors=5,weights=’uniform’,algorithm=’auto’,leaf_size=30,p=2,metric=’minkowski’,metric_params=None,n_jobs=1,**kwargs)
参数说明：

n_neighbors: int, 可选参数(默认为 5)用于kneighbors查询的默认邻居的数量

weights（权重）: str or callable(自定义类型), 可选参数(默认为 ‘uniform’)

用于预测的权重函数。可选参数如下:

‘uniform’ : 统一的权重. 在每一个邻居区域里的点的权重都是一样的。

‘distance’ : 权重点等于他们距离的倒数。使用此函数，更近的邻居对于所预测的点的影响更大。

[callable] : 一个用户自定义的方法，此方法接收一个距离的数组，然后返回一个相同形状并且包含权重的数组。

algorithm（算法）: {‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}, 可选参数（默认为 ‘auto’）

计算最近邻居用的算法：

‘ball_tree’ 是为了克服kd树高纬失效而发明的，其构造过程是以质心C和半径r分割样本空间，每个节点是一个超球体。

‘kd_tree’ 构造kd树存储数据以便对其进行快速检索的树形数据结构，kd树也就是数据结构中的二叉树。以中值切分构造的树，每个结点是一个超矩形，在维数小于20时效率高。

‘brute’ 使用暴力搜索.也就是线性扫描，当训练集很大时，计算非常耗时

‘auto’ 会基于传入fit方法的内容，选择最合适的算法。

leaf_size（叶子数量）: int, 可选参数(默认为 30)

传入BallTree或者KDTree算法的叶子数量。此参数会影响构建、查询BallTree或者KDTree的速度，以及存储BallTree或者KDTree所需要的内存大小。此可选参数根据是否是问题所需选择性使用。

p: integer, 可选参数(默认为 2)

用于Minkowski metric（闵可夫斯基空间）的超参数。p = 1, 相当于使用曼哈顿距离 (l1)，p = 2, 相当于使用欧几里得距离(l2) 对于任何 p ，使用的是闵可夫斯基空间(l_p)

metric（矩阵）: string or callable, 默认为 ‘minkowski’

用于树的距离矩阵。默认为闵可夫斯基空间，如果和p=2一块使用相当于使用标准欧几里得矩阵. 所有可用的矩阵列表请查询 DistanceMetric 的文档。

metric_params（矩阵参数）: dict, 可选参数(默认为 None)

给矩阵方法使用的其他的关键词参数。

n_jobs: int, 可选参数(默认为 1)

用于搜索邻居的，可并行运行的任务数量。如果为-1, 任务数量设置为CPU核的数量。不会影响fit方法。

方法：

方法名	含义
fit(X, y)	使用X作为训练数据，y作为目标值（类似于标签）来拟合模型。
get_params([deep])	获取估值器的参数。
kneighbors([X, n_neighbors, return_distance])	查找一个或几个点的K个邻居。
kneighbors_graph([X, n_neighbors, mode])	计算在X数组中每个点的k邻居的（权重）图。
predict(X)	给提供的数据预测对应的标签。
predict_proba(X)	返回测试数据X的概率估值。
score(X, y[, sample_weight])	返回给定测试数据和标签的平均准确值。
set_params(**params)	设置估值器的参数。

init(n_neighbors=5,weights=’uniform’,algorithm=’auto’,leaf_size=30,p=2,metric=’minkowski’,metric_params=None,n_jobs=1,*kwargs)
fit(X,y):
- 使用X作为训练数据，y作为目标值（标签）拟合模型
  参数:
  
  X: {类似数组, 稀疏矩阵, BallTree, KDTree}
  
  待训练数据。如果是数组或者矩阵，形状为 [n_samples, n_features]，如果矩阵为’precomputed’, 则形状为[n_samples, n_samples]。
  
  y: {类似数组, 稀疏矩阵}
  
  形状为[n_samples] 或者 [n_samples, n_outputs]的目标值。
get_params(deep=True)
- 获取估值器的参数.
  参数:
  
  deep: boolean, 可选参数
  
  如果为 True, 则返回估值器的参数，以及包含子目标的估值器。
  
  返回值:
  
  params: Mapping string to any
  
  返回Map变量，内容为[参数值: 值, 参数值: 值, …]。
kneighbors(X=None,n_neighbors=None,return_distance=True)[source]
- 查询一个或几个点的K个邻居, 返回每个点的下标和到邻居的距离。
  （重点使用）
  
  参数:
  
  X: 类似数组, 形状(n_query, n_features)或者(n_query, n_indexed) 。
  
  如果矩阵是‘precomputed’，形状为(n_query, n_indexed)带查询的一个或几个点。如果没有提供，则返回每个有下标的点的邻居们。
  
  n_neighbors: int
  
  邻居数量 (默认为调用构造器时设定的n_neighboes的值).
  
  return_distance: boolean, 可选参数. 默认为 True.
  
  如果为 False，则不会返回距离
  
  返回值:
  
  dist: array
  
  当return_distance =True时，返回到每个点的长度。
  
  ind: array
  
  邻居区域里最近的几个点的下标。
  
  例子：
  
  在此案例中, 我们构建了一个NeighborsClassifier类。此类从数组中获取数据，并查询哪个点最接近于[1, 1, 1]
```
samples = [[0., 0., 0.], [0., .5, 0.], [1., 1., .5]]
from sklearn.neighbors import NearestNeighbors
neigh = NearestNeighbors(n_neighbors=1)
neigh.fit(samples)
NearestNeighbors(algorithm='auto', leaf_size=30, ...)
print(neigh.kneighbors([[1., 1., 1.]]))# >> (array([[ 0.5]]), array([[2]]...))""" 如你所见返回值为[[0.5]] 和 [[2]]。意思是此点是距离为0.5并且是样本中的第三个元素 (下标从0开始)。你可以尝试查询多个点： """
X = [[0., 1., 0.], [1., 0., 1.]]
neigh.kneighbors(X, return_distance=False)array([[1], [2]]...)
```
kneighbors_graph(X=None,n_neighbors=None,mode=’connectivity’)[source]
- 计算在X数组中每个点的k邻居的（权重）
  
  参数:
  
  X: 类似数组, 形状(n_query, n_features)。
  
  如果矩阵是‘precomputed’，形状为(n_query, n_indexed)一个或多个待查询点。如果没有提供，则返回每个有下标的点的邻居们。
  
  n_neighbors: int
  
  邻居数量。(默认为调用构造器时设定的n_neighboes的值)。
  
  mode: {‘connectivity’, ‘distance’}, 可选参数
  
  返回矩阵数据类型： ‘connectivity’ 会返回1和0组成的矩阵。 in ‘distance’ 会返回点之间的欧几里得距离。
  
  返回值:
  
  A: CSR格式的稀疏矩阵，形状为 [n_samples, n_samples_fit]
  
  n_samples_fit 是拟合过的数据中样例的数量，其中 A[i, j] 代表i到j的边的权重。
  
  例子：
```
X=[[0], [3], [1]]
from sklearn.neighbors import NearestNeighbors
neigh=NearestNeighbors(n_neighbors=2) neigh.fit(X)
NearestNeighbors(algorithm='auto', leaf_size=30, ...)
A=neigh.kneighbors_graph(X)
A.toarray()
""" array([[ 1., 0., 1.],[ 0., 1., 1.],[ 1., 0., 1.]]) """
```
predict(X)[source]
- 给提供的数据预测相应的类别标签
  
  参数:
  
  X: 类似数组, 形状(n_query, n_features)。
  
  如果矩阵是‘precomputed’，形状为(n_query, n_indexed) 待测试样例。
  
  返回值:
  
  y: 形状为 [n_samples] 或者 [n_samples, n_outputs]的数组
  
  返回每个待测试样例的类别标签。
predict_proba(X)[source]
- 返回测试数据X的概率估值。
  参数:
  
  X: 类似数组, 形状(n_query, n_features)。
  
  如果矩阵是‘precomputed’，形状为(n_query, n_indexed)待测试样例。
  
  返回值:
  
  p: 形状为[n_samples, n_classes]的数组，或者是n_outputs列表
  
  输入样例的类别概率估值。其中类别根据词典顺序排序。
score(X, y, sample_weight=None)[source]
- 返回给定测试数据和标签的平均准确度。在多标签分类中，返回的是各个子集的准确度。
  
  参数:
  
  X : 类似数组，
  
  形状为 (n_samples, n_features)待测试样例
  
  y: 类似数组，
  
  形状为 (n_samples) 或者 (n_samples, n_outputs)X对于的正确标签
  
  sample_weight: 类似数组，
  
  形状为 [n_samples], 可选参数待测试的权重
  
  返回值:
  
  score : float
  
  self.predict(X) 关于y的平均准确率。
set_params(**params)[source]
- 设置估值器的参数。
  
  此方法在单个估值器和嵌套对象（例如管道）中有效。而嵌套对象有着__形式的参数，方便更新各个参数。