题目地址:https://vjudge.net/problem/UVALive-4992
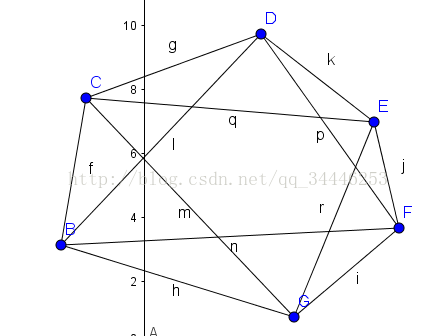
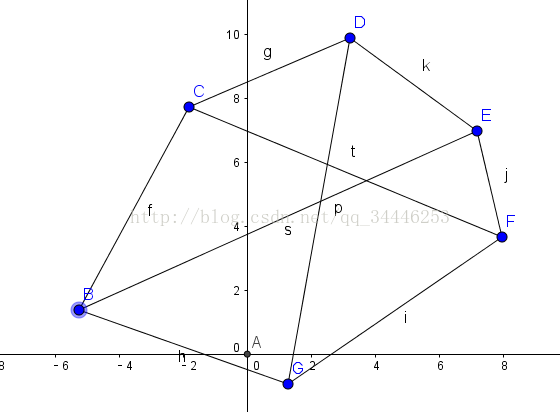
间隔一个点的所有线段连起来求半平面交,
间隔两个点的所有线段连起来求半平面交,
。。。
直到刚好不存在半平面交,就是答案
可以用二分来查找答案
#include <bits/stdc++.h>
using namespace std;
#define REP(i,a,b) for(int i=a;i<=(int)(b);++i)
#define REPD(i,a,b) for(int i=a;i>=(int)(b);--i)
const double PI=acos(-1);
const double EPS=1e-6; //1e-6 WR
int dcmp(double x){if(fabs(x)<EPS) return 0;return x > 0 ? 1 : -1;
}
struct Point{double x,y;Point(double x=0,double y=0):x(x),y(y){}
};
typedef Point Vector;
bool operator < (const Point& p1, const Point& p2){ return p1.x<p2.x || (p1.x==p2.x && p1.y<p2.y) ;}
Vector operator / (const Point& A, double x){ return Vector{A.x/x, A.y/x};}
Vector operator * (const Vector& A, double x){ return Vector{A.x*x, A.y*x};}
Vector operator - (const Vector& A, const Vector& B){ return Vector{A.x-B.x,A.y-B.y};}
Vector operator + (const Point& A, const Vector& v){ return Point{A.x+v.x,A.y+v.y};}
Vector Rotate(const Point& p,double ang){ return Vector{p.x*cos(ang)-p.y*sin(ang),p.x*sin(ang)+p.y*cos(ang)};}
double Cross(const Vector& A, const Vector& B){ return A.x*B.y-A.y*B.x;}
double Dot(Vector A, Vector B){ return A.x*B.x+A.y*B.y;}
double Length(Vector v){ return sqrt(fabs(Dot(v,v)));}
Vector Unit(Vector v){ return v/Length(v);}struct Line
{Point p; Vector v; double ang;Line(){}Line(Point p, Vector v) : p(p),v(v) { ang=atan2(v.y,v.x); }bool operator < (const Line& l) const{return ang < l.ang;}
};
const int maxn=50000+5;
Line L[maxn];
Point p[maxn];
bool OnLeft(Point p, Line L){return dcmp(Cross(L.v, p-L.p)) > 0;
}
Point GetPInter(Line a, Line b){Vector u=a.p-b.p;double t=Cross(u,a.v) / Cross(b.v,a.v);return b.p+b.v*t;
}
bool halfplaneIntersection(Line* A, int n){sort(A,A+n);int i,j;Line* Q = new Line[n];Point* p = new Point[n];Q[i=j=0]=A[0];REP(k,1,n-1) {while(i<j && !OnLeft(p[j-1], A[k])) j--;while(i<j && !OnLeft(p[i], A[k])) i++;Q[++j]=A[k];if(dcmp(Cross(Q[j].v, Q[j-1].v))==0){j--;if(OnLeft(Q[j+1].p, Q[j])) Q[j]=Q[j+1];}if(i<j) p[j-1]=GetPInter(Q[j-1], Q[j]);}while(i<j && !OnLeft(p[j-1], Q[i])) j--;if(j-i<=1) return false; //交集为空,平面就存在两个点以内(线段或点)return true;
}
int main(int argc, char const *argv[])
{// freopen("input.in","r",stdin);int n;while(scanf("%d",&n)==1&&n){REPD(i,n-1,0) scanf("%lf%lf",&p[i].x,&p[i].y);int l=1,r=n;while(r>l){int mid=l+((r-l)>>1);int cnt=0;REP(i,0,n-1) L[cnt++]=Line(p[i],p[(i+mid+1)%n]-p[i]);if(!halfplaneIntersection(L,cnt)) r=mid;else l=mid+1;}printf("%d\n", l);}return 0;
}