一、前言
根据王道讲解和网上资料,总结的红黑树相关知识点和考点。
可能考:红黑树的性质、插入、删除(选择题,代码可能不考,略复杂)
二、红黑树
(一)定义
1. 红黑树是实质上是一棵自平衡的二叉查找树,有时形态不一定是平衡二叉树。
(左子树结点值 < 根结点值 < 右子树结点值)
2. 引入带颜色的节点也是为了方便在进行插入或删除操作时,如果破坏了二叉查找树的平衡性能通过一系列变换保持平衡。
3. 红黑树的查找、插入、删除的时间复杂度均为。
(注意:AVL的查找、插入、删除的时间复杂度也是均为)
4. 适用于频繁插入、删除的场景,实用性更强。(对于平衡二叉树AVL,适用以查找为主,很少插入、删除的场景)
(二)性质(5个)
1. 结点是红色或黑色;
2. 根结点是黑色。
3. 叶子结点(也叫外部结点、NULL结点、失败结点)是黑色。
4. 不存在两个相邻的红结点。(即红结点的父结点和子结点都是黑色的)
5. 从任意结点到可达的叶子结点的每个路径包含相同数目的黑色节点。
(三)结论(2个)
结论1:从根到叶结点的最长路径不大于最短路径的2倍。
结论2:有 n 个内部结点的红黑树的高度
(四)上口诀来理解红黑树的性质
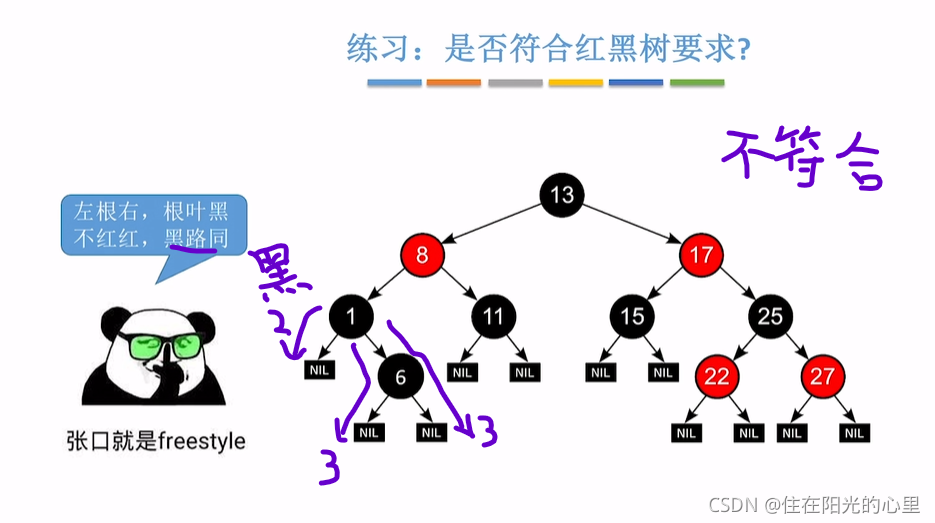
“口诀1”:左根右,根叶黑,不红红,黑路同。(源自王道)
“口诀2”:(这是博主改编的,纯属为了好记,大家可自行选择)
大小左根右,根叶结点黑(性质2+3),父子不红红(性质4),路路同黑数(性质5)。
(注意:选择题若考选择哪一棵树是红黑树,就用口诀查证,看是否条条符合)
加深理解:
“黑路同”:一条路走到黑,从任意的结点出发,到失败结点,都具有相同的黑结点数。
例如:下图中,从结点1出发,到左结点NIL的黑结点个数为2;到右子树的结点NIL的黑结点个数都为3;黑色结点数不相同,所以该树不是红黑树。
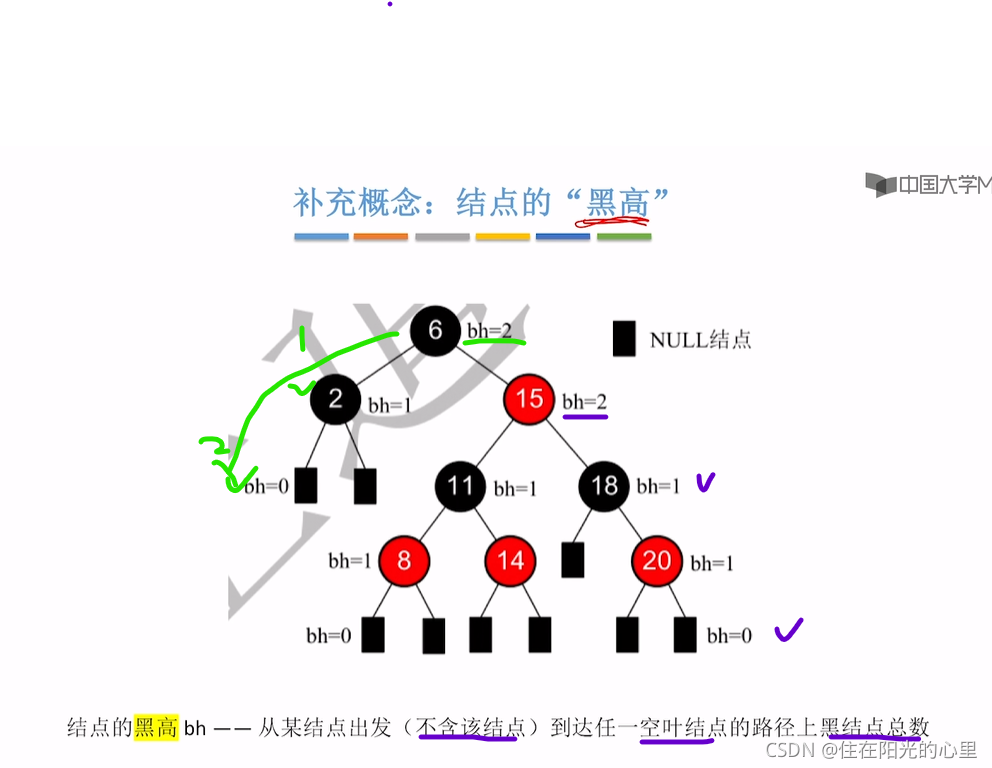
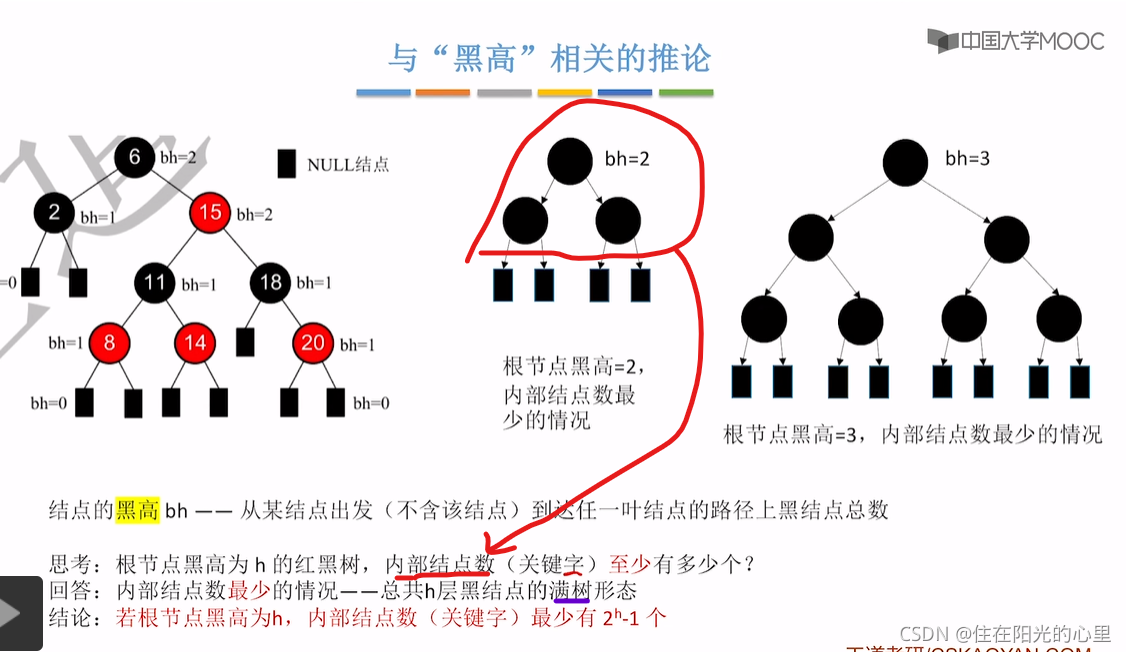
补充:根节点黑高为h的红黑树,内部结点数(关键字)至多有 个。
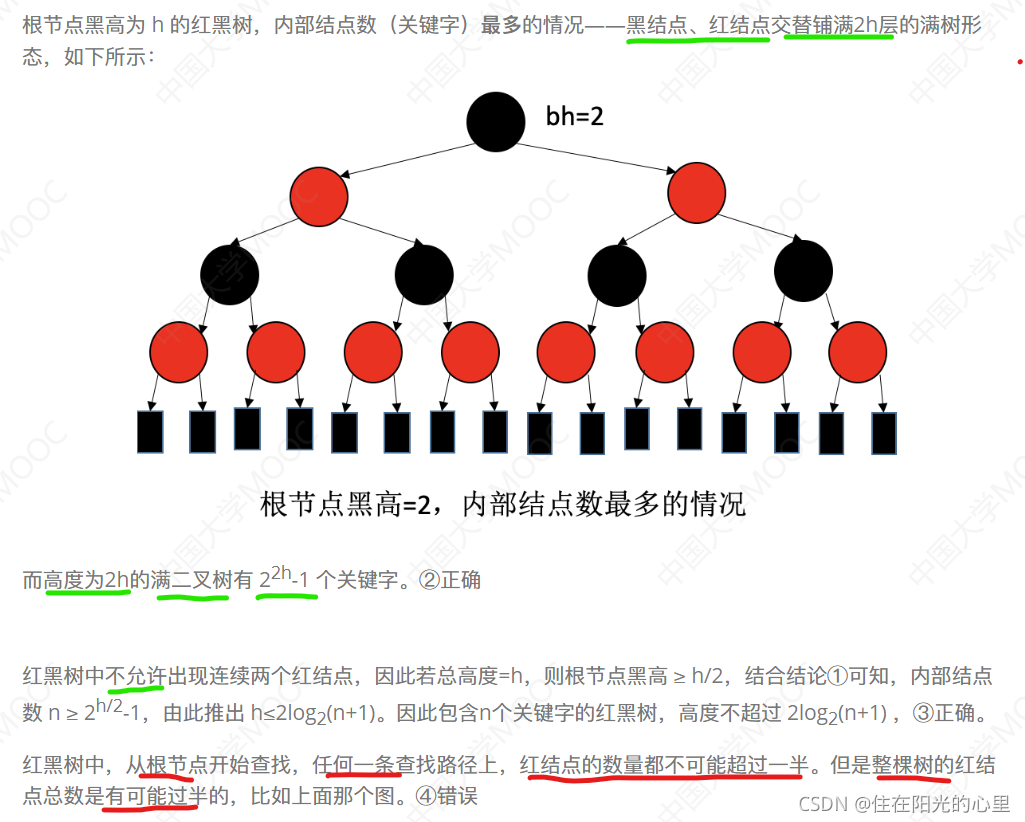

(五)结点定义的代码
// 红黑树的结点定义
struct RBnode{int key; // 关键字的值RBnode *parent; // 父节点的指针RBnode *lChild; // 左孩子的指针RBnoce *rChild; // 右孩子的指针int color; // 结点颜色,如可用 0/1 表示 黑/红。也可用枚举型 enum 表示颜色。
};(六)红黑树的插入
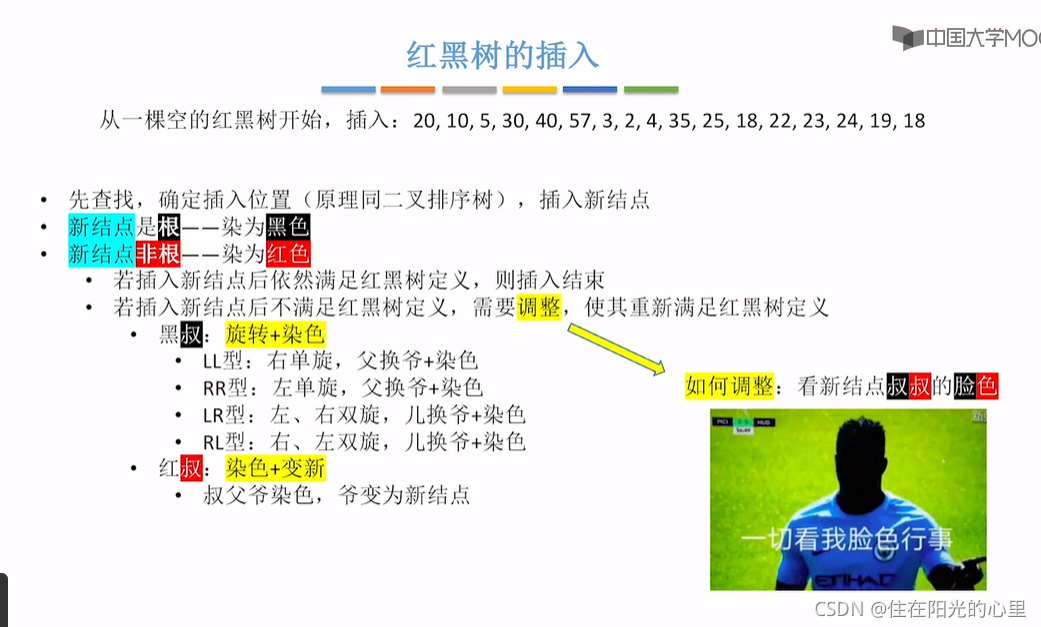
可以结合下面的例子来理解:
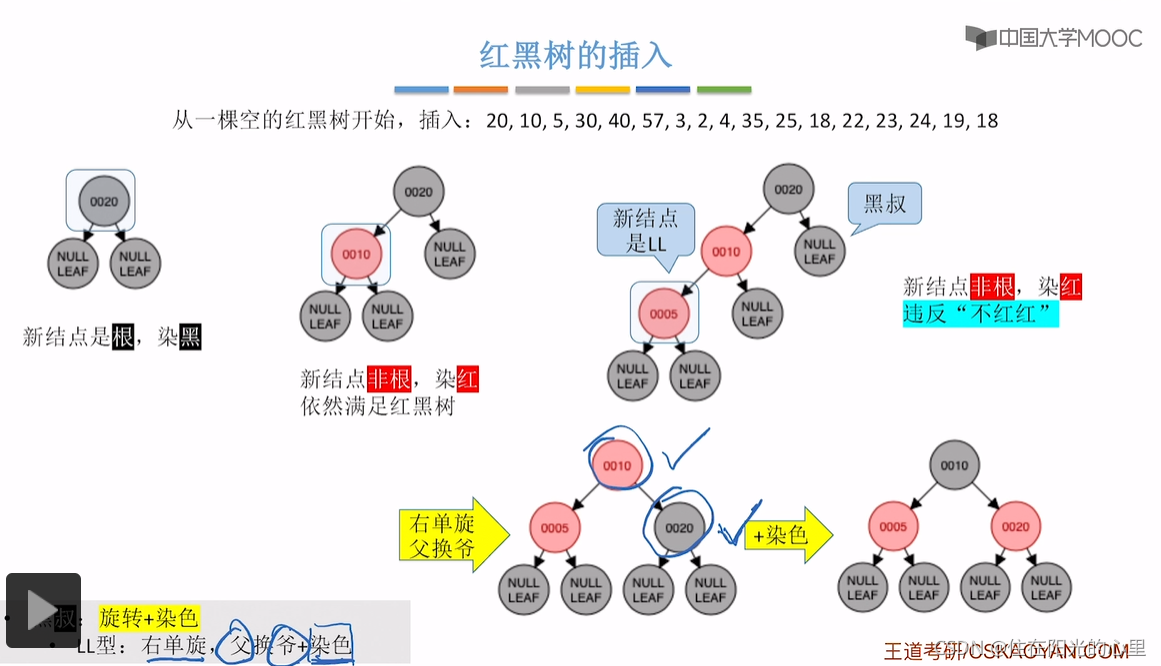
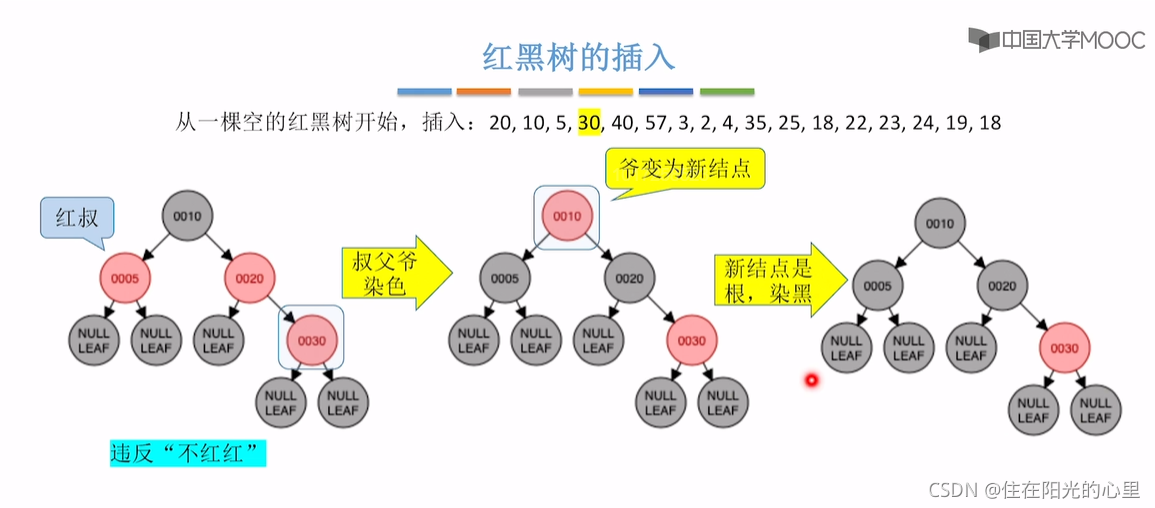
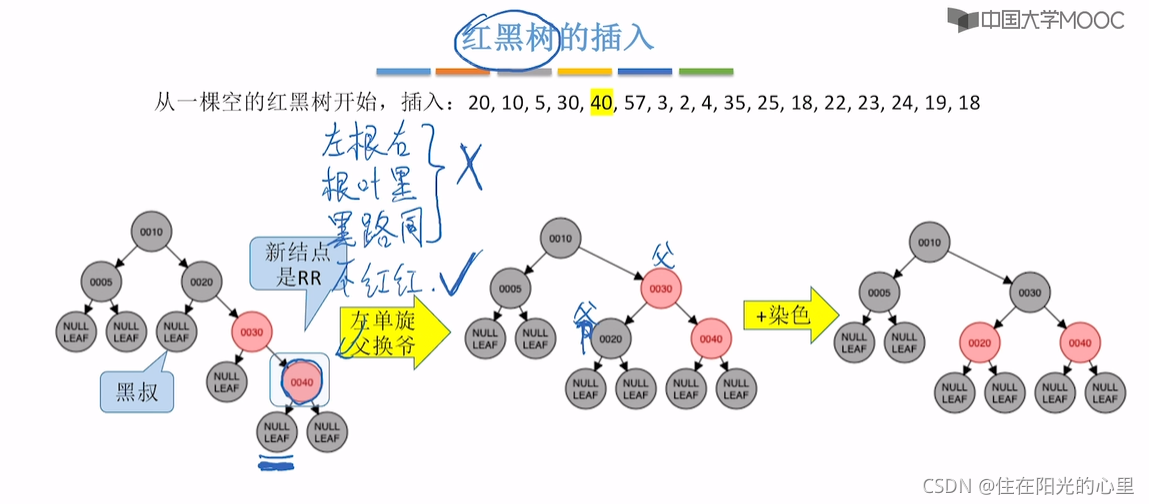
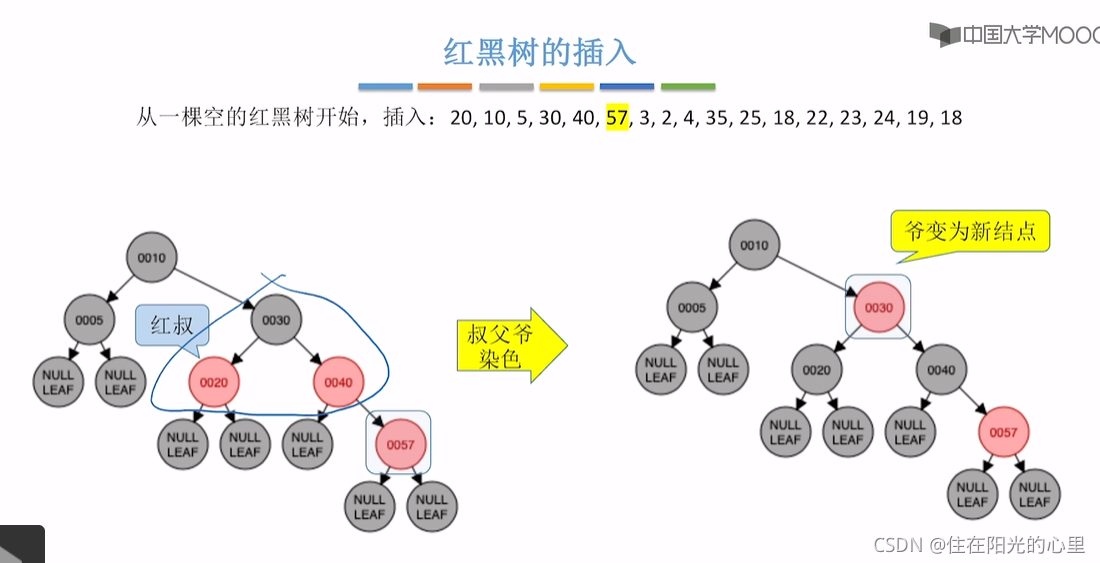
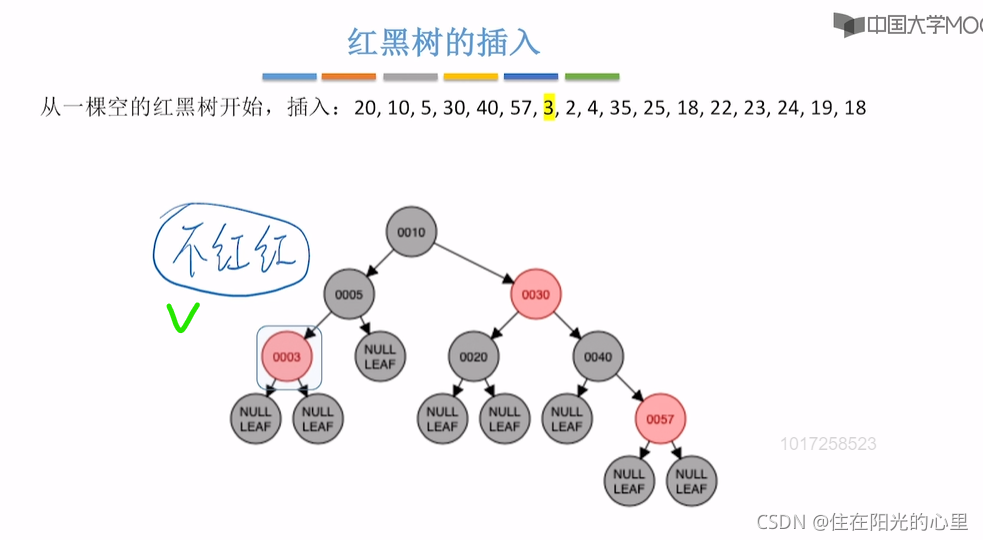
注意:红黑树的插入,并不用考虑是否满足“左根右,根叶黑,黑路同”的条件。 只需考虑是否破坏了“不红红”的特点,如果父子都是红结点,则按“红叔”、“黑叔”的划分进行下一步。
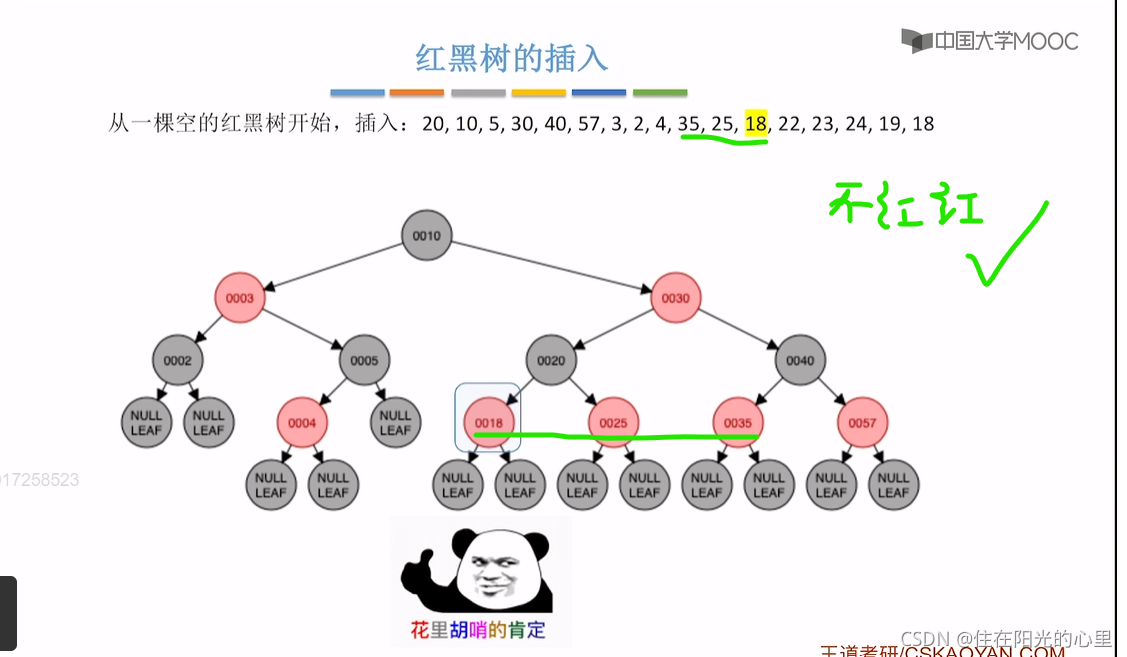
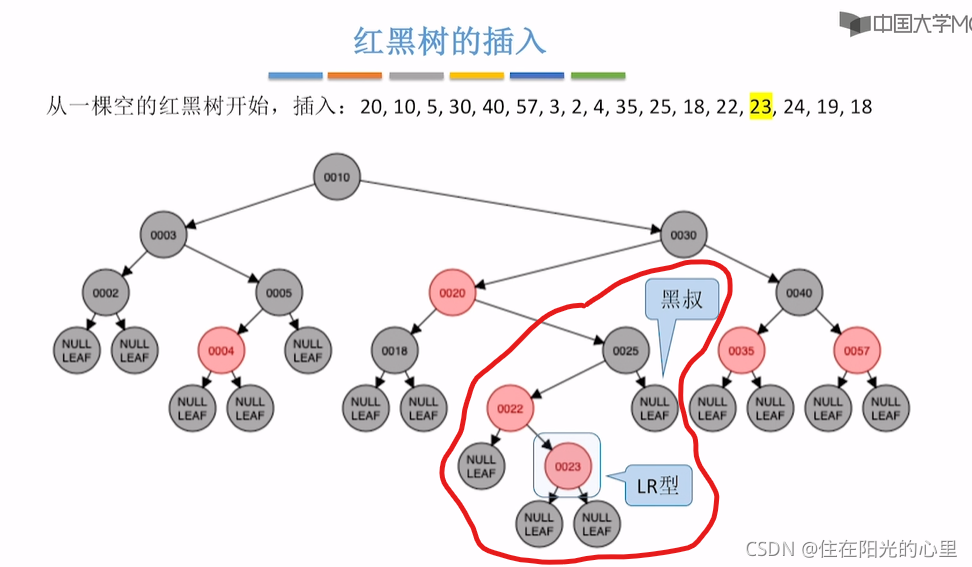
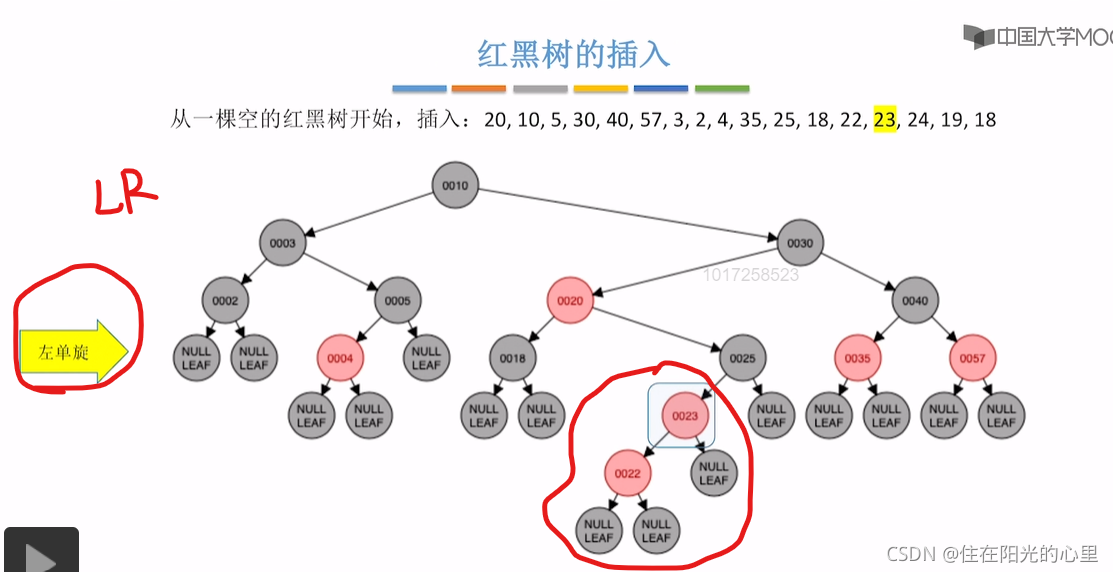
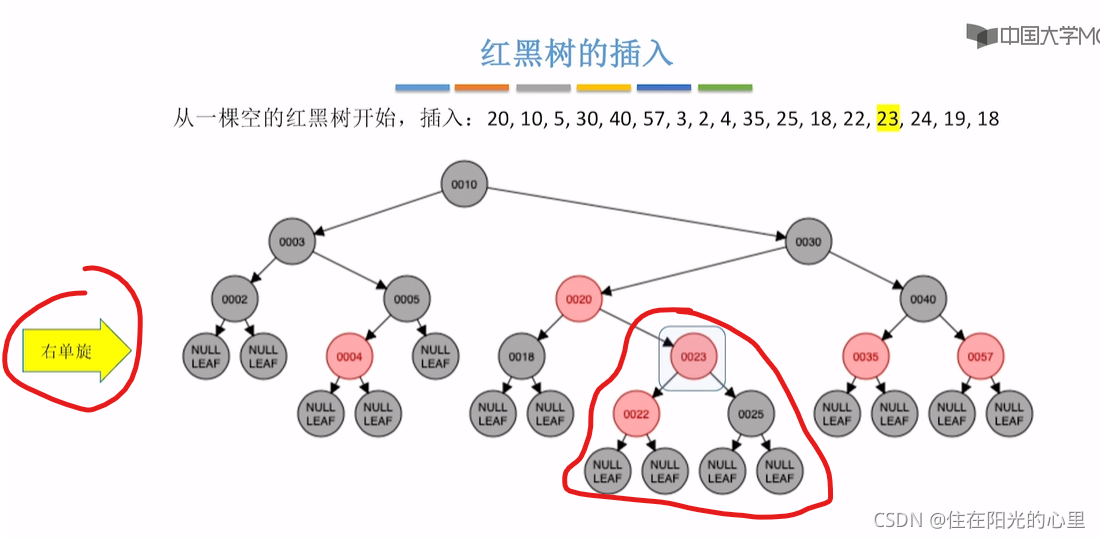
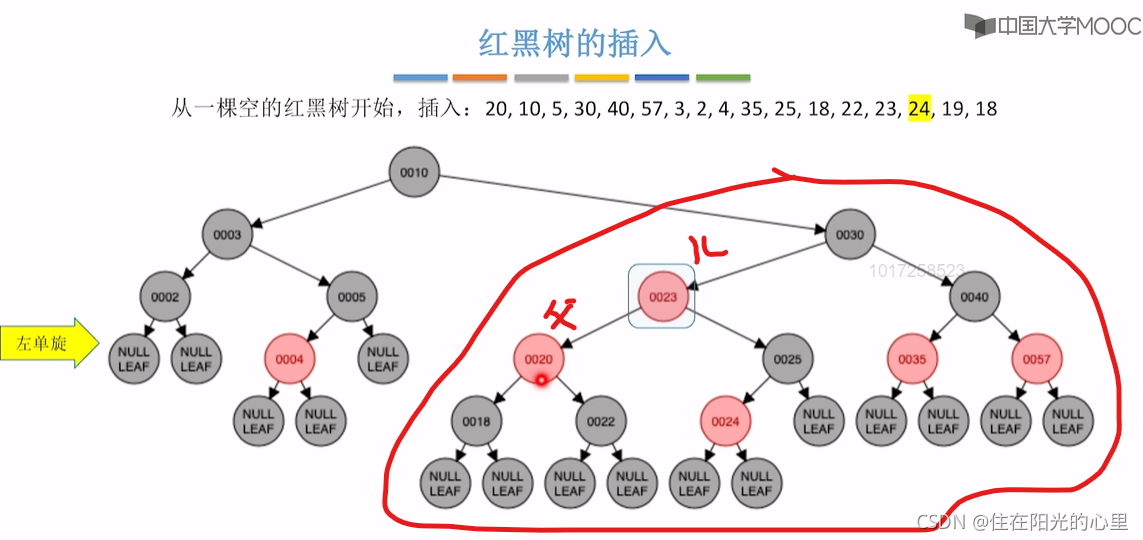
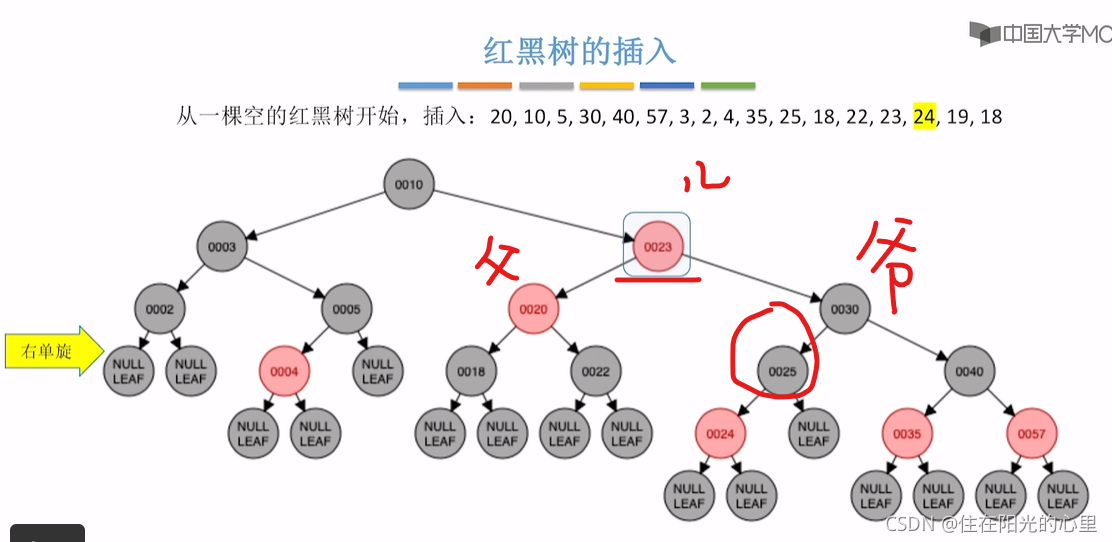
可以看到上图,插入23结点后,违背了“不红红”,结点23的父亲的兄弟结点是黑色,即黑叔。而结点23是“LR”型,则先进行左单旋,再右单旋,再将结点23(儿子)和结点25(爷爷)染色(即23红变黑,25黑变红)。(右单旋的结果:是儿子辈分升高再升高。)
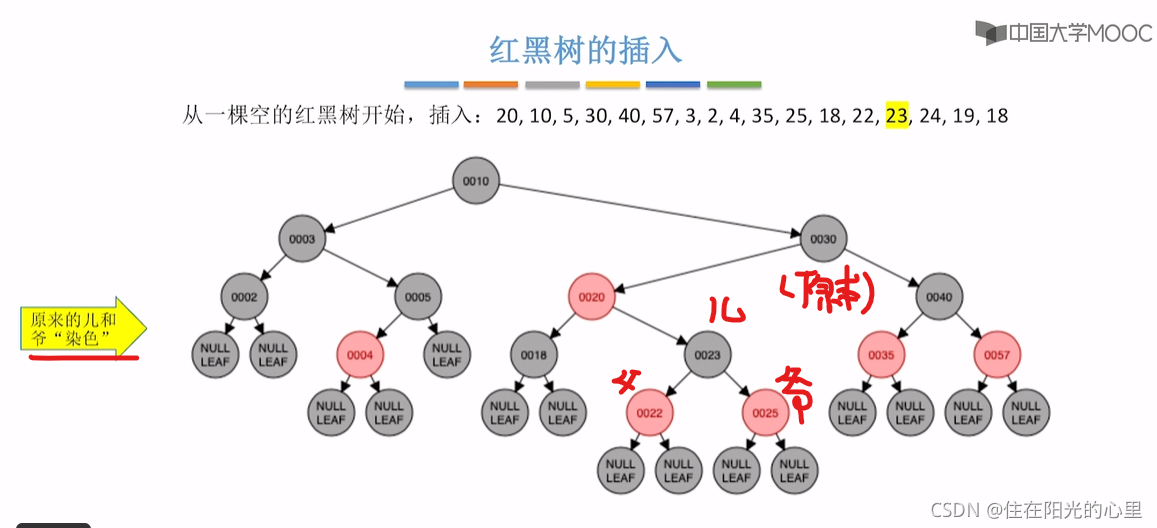
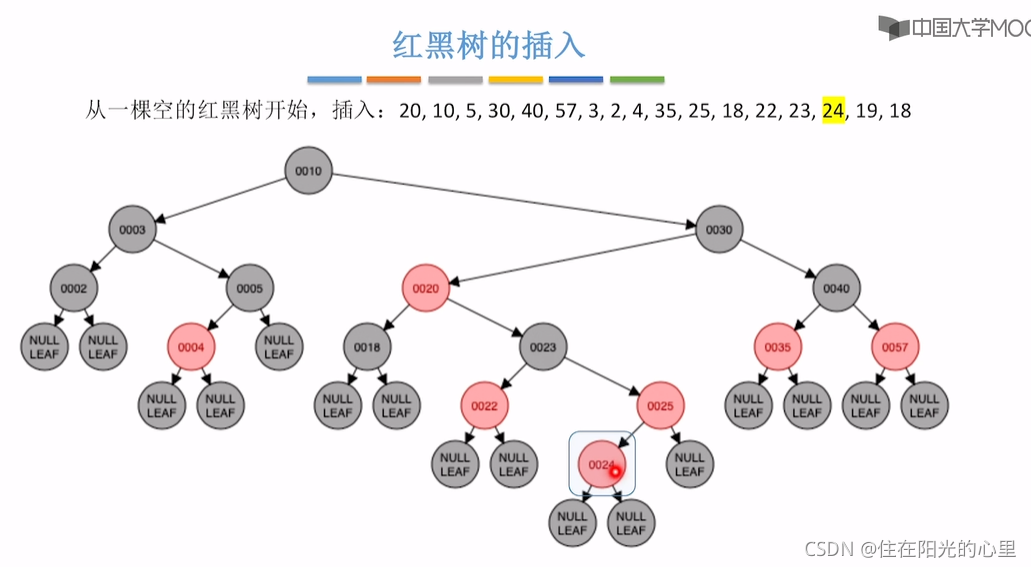
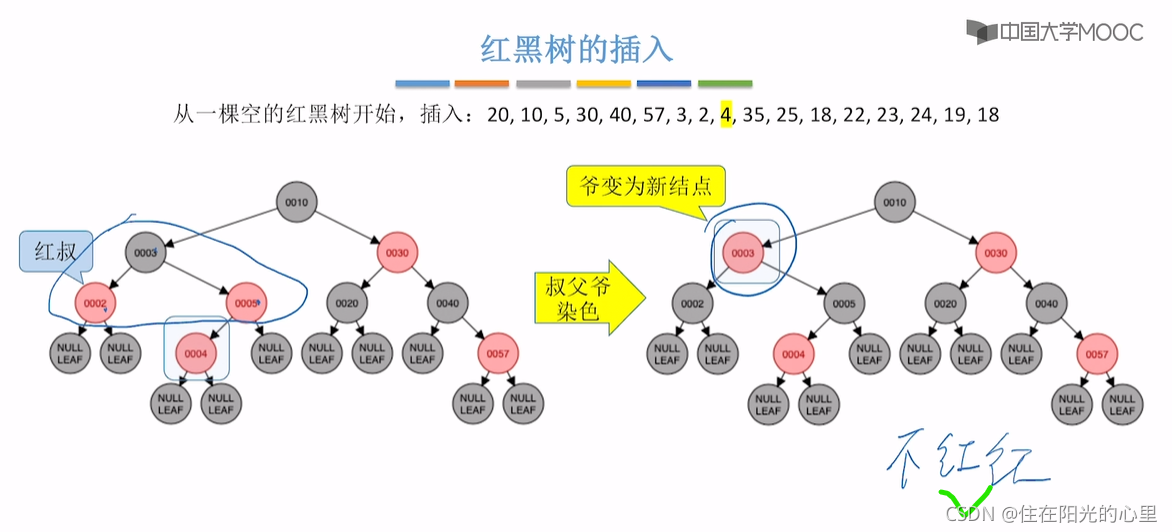
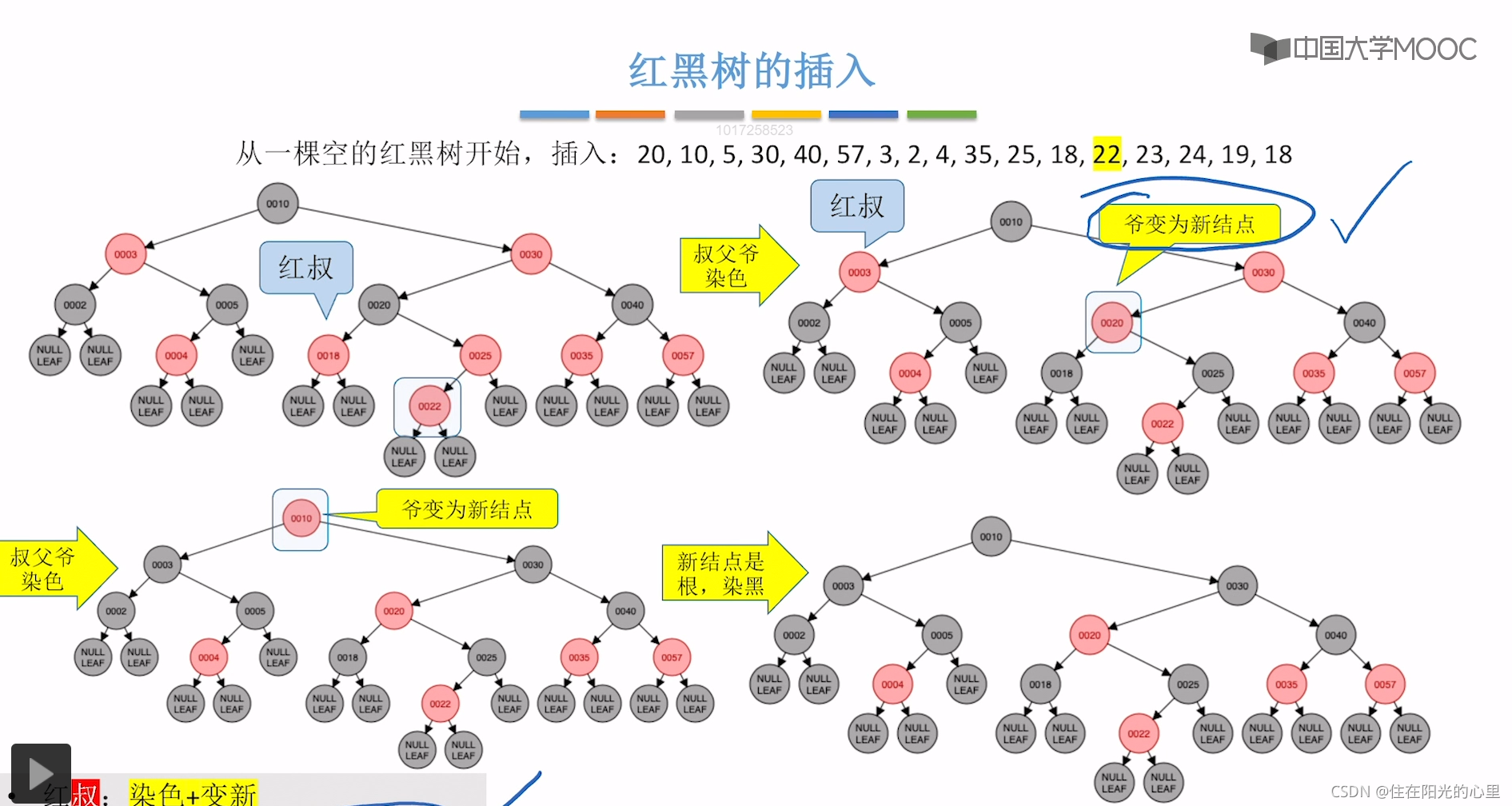
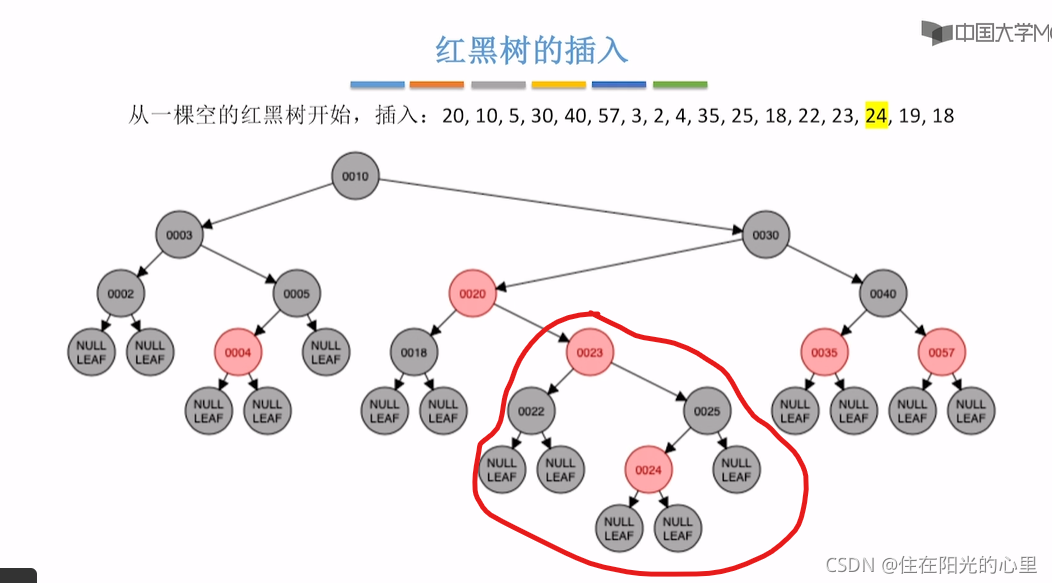
上图插入结点24后,违背“不红红”,则看其叔为结点22,是红色,“红叔”则“染色+变新”,叔父爷染色,爷变新结点。
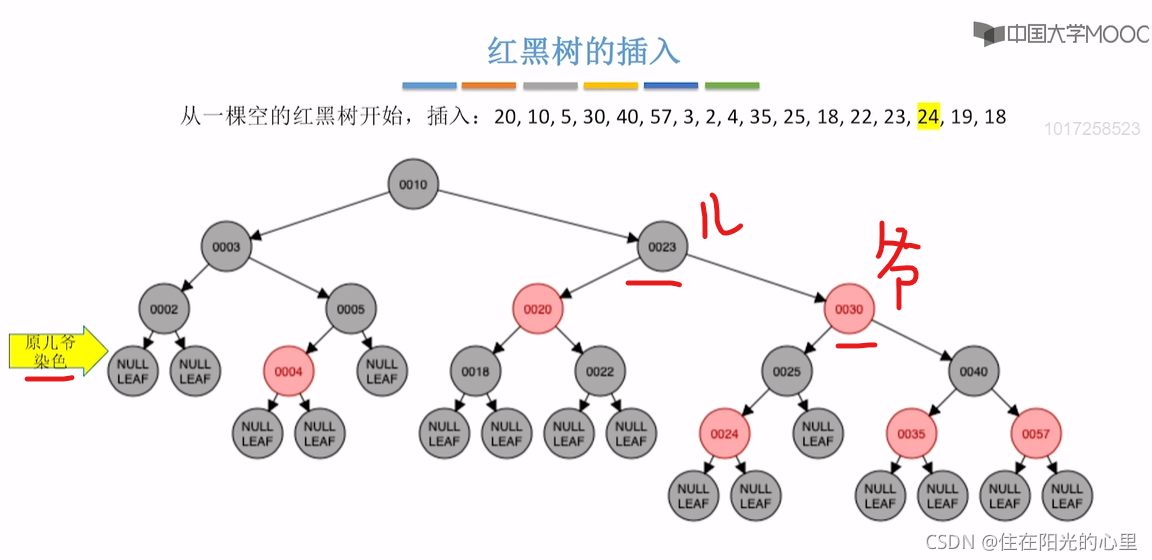
如下图,但结点20和23违背了 “不红红”,则看结点23的叔为结点40,是黑色。
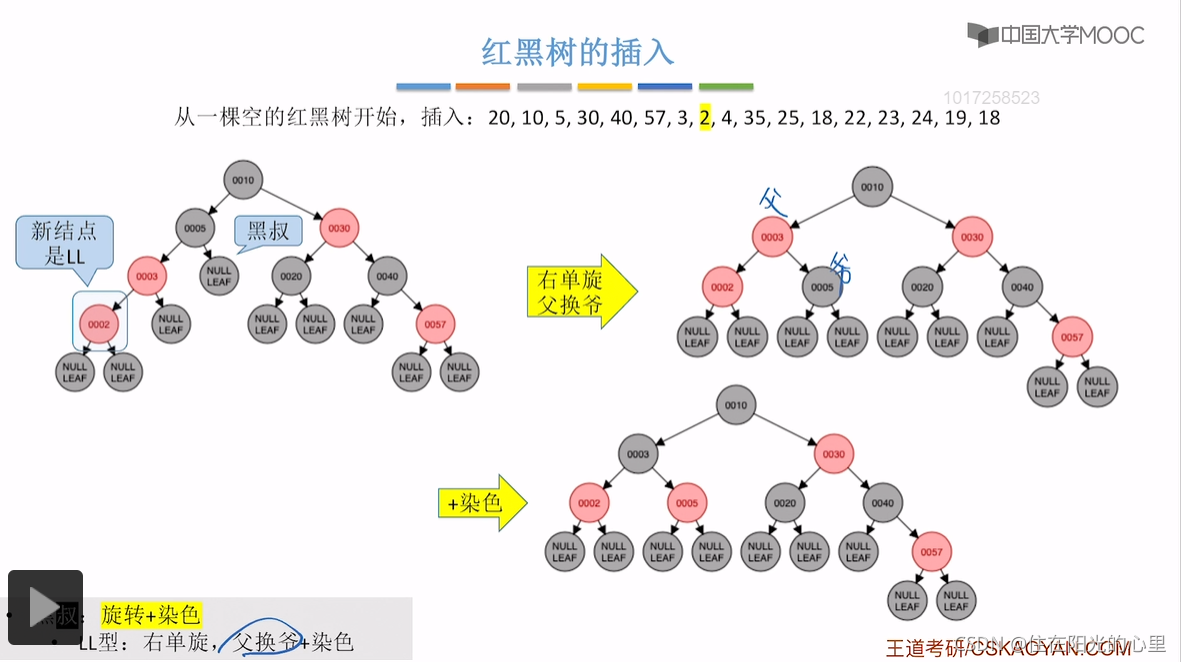
黑叔:旋转+染色(LR型:左、右双旋,儿换爷+染色)
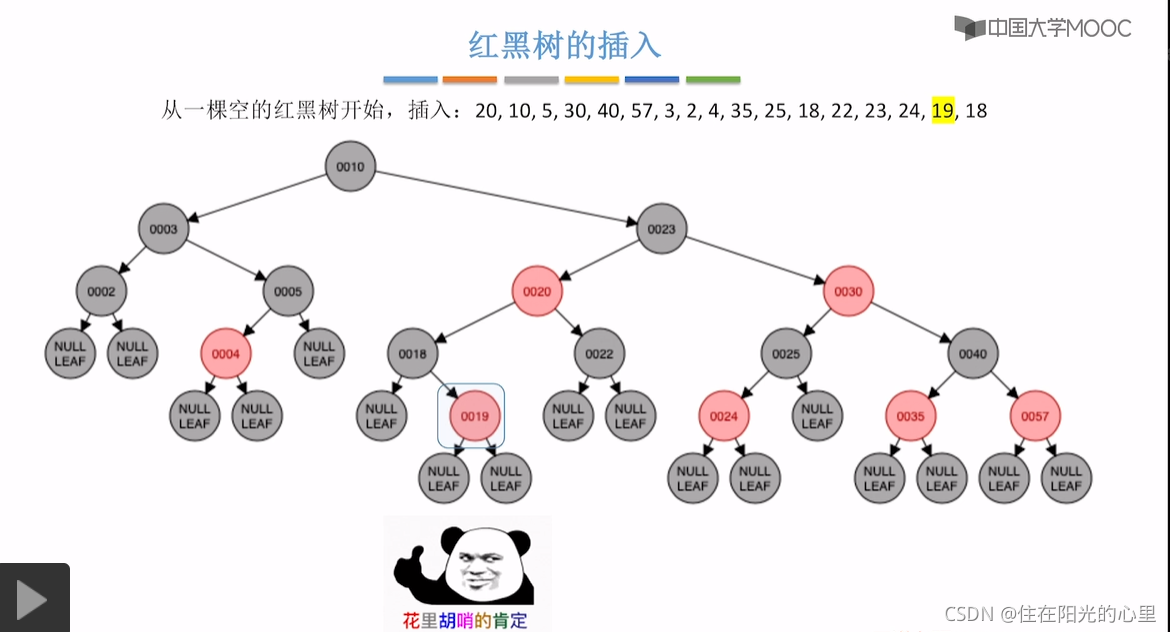
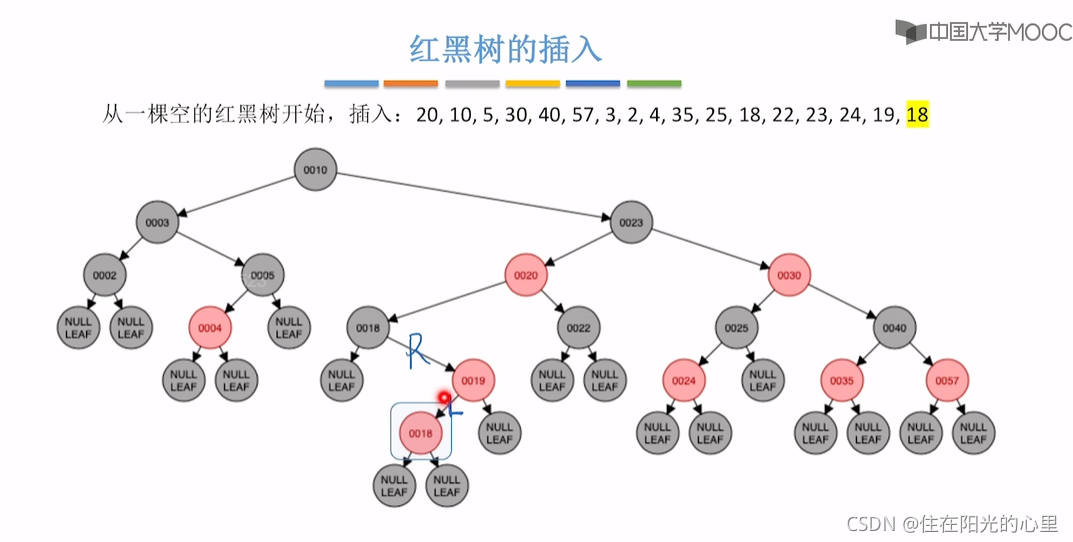
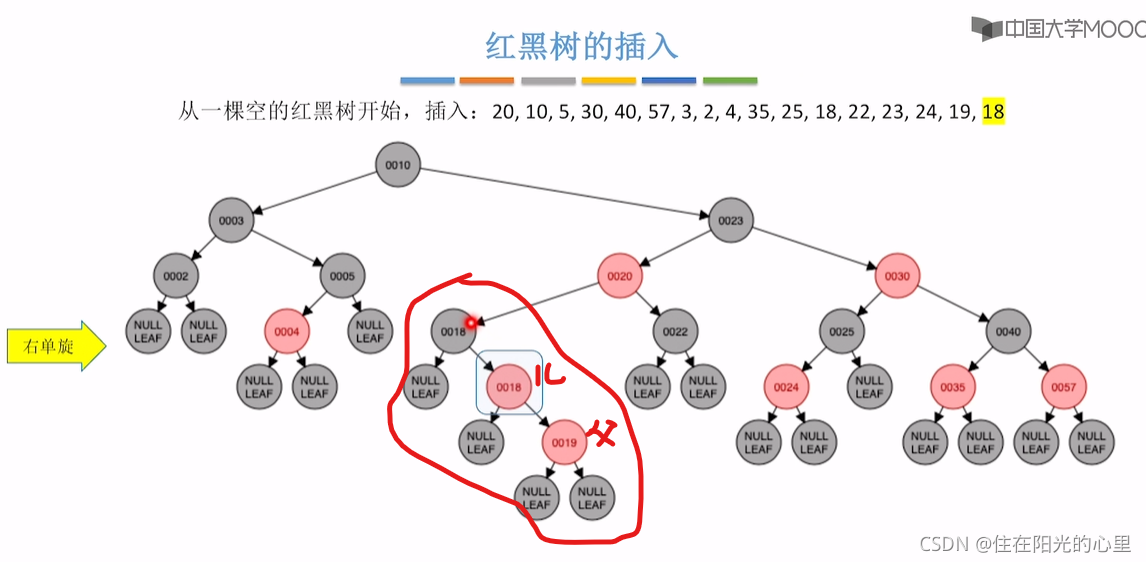
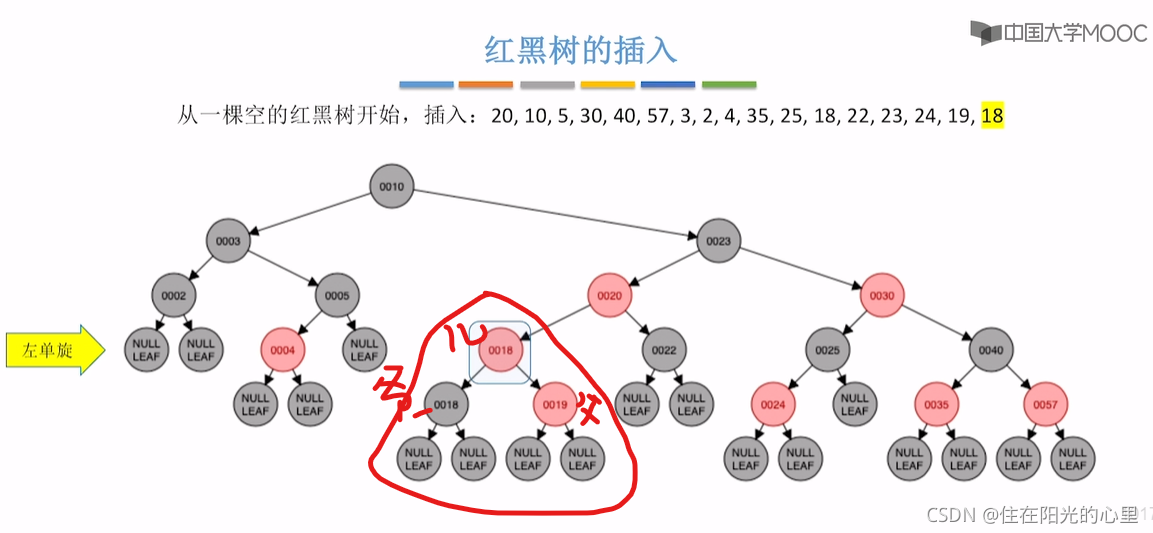
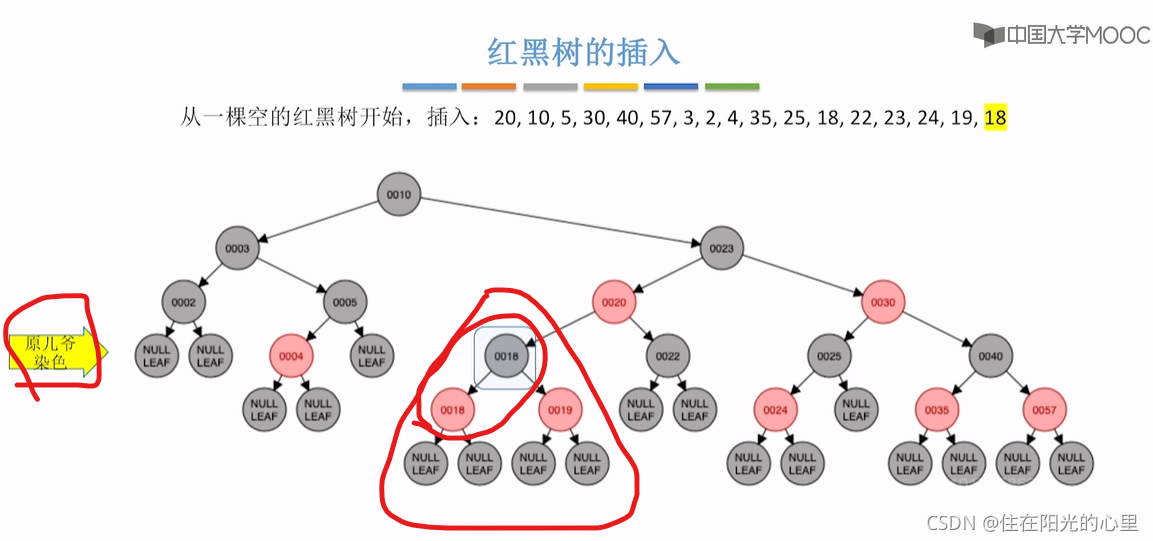
最后一步插入18时,18是重复的关键字,可以插在第一个18结点的左子树,也可插入到右子树中,下面示范的是插入到第一个18结点的右子树。那么第二个18结点,是RL型,其叔是黑色。
黑叔:旋转+染色(RL型:右、左双旋,儿换爷+染色)
(七)总结:
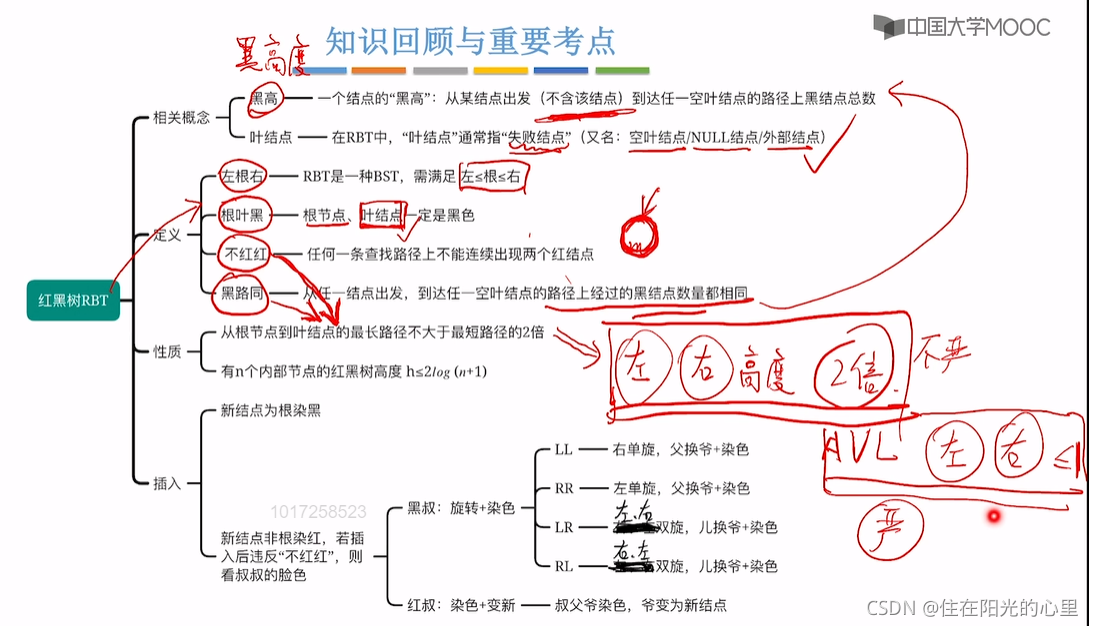
备注:可参考以下网址来学习
种树:二叉树、二叉搜索树、AVL树、红黑树、哈夫曼树、B树、树与森林_看,未来的博客-CSDN博客_哈夫曼树和红黑树