1.Encoder-Decoder模型及RNN的实现
所谓encoder-decoder模型,又叫做编码-解码模型。这是一种应用于seq2seq问题的模型。
那么seq2seq又是什么呢?简单的说,就是根据一个输入序列x,来生成另一个输出序列y。seq2seq有很多的应用,例如翻译,文档摘取,问答系统等等。在翻译中,输入序列是待翻译的文本,输出序列是翻译后的文本;在问答系统中,输入序列是提出的问题,而输出序列是答案。
为了解决seq2seq问题,有人提出了encoder-decoder模型,也就是编码-解码模型。所谓编码,就是将输入序列转化成一个固定长度的向量;解码,就是将之前生成的固定向量再转化成输出序列。
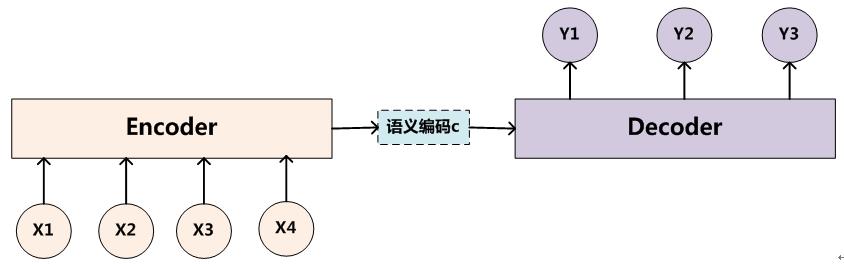
当然了,这个只是大概的思想,具体实现的时候,编码器和解码器都不是固定的,可选的有CNN/RNN/BiRNN/GRU/LSTM等等,你可以自由组合。比如说,你在编码时使用BiRNN,解码时使用RNN,或者在编码时使用RNN,解码时使用LSTM等等。
这边为了方便阐述,选取了编码和解码都是RNN的组合。在RNN中,当前时间的隐藏状态是由上一时间的状态和当前时间输入决定的,也就是
获得了各个时间段的隐藏层以后,再将隐藏层的信息汇总,生成最后的语义向量
一种简单的方法是将最后的隐藏层作为语义向量C,即
解码阶段可以看做编码的逆过程。这个阶段,我们要根据给定的语义向量C和之前已经生成的输出序列y1,y2,…yt?1来预测下一个输出的单词yt,即
也可以写作
而在RNN中,上式又可以简化成
其中s是输出RNN中的隐藏层,C代表之前提过的语义向量,yt?1表示上个时间段的输出,反过来作为这个时间段的输入。而g则可以是一个非线性的多层的神经网络,产生词典中各个词语属于yt的概率。
encoder-decoder模型虽然非常经典,但是局限性也非常大。最大的局限性就在于编码和解码之间的唯一联系就是一个固定长度的语义向量C。也就是说,编码器要将整个序列的信息压缩进一个固定长度的向量中去。但是这样做有两个弊端,一是语义向量无法完全表示整个序列的信息,还有就是先输入的内容携带的信息会被后输入的信息稀释掉,或者说,被覆盖了。输入序列越长,这个现象就越严重。这就使得在解码的时候一开始就没有获得输入序列足够的信息, 那么解码的准确度自然也就要打个折扣了
2.Attention模型
为了解决这个问题,作者提出了Attention模型,或者说注意力模型。简单的说,这种模型在产生输出的时候,还会产生一个“注意力范围”表示接下来输出的时候要重点关注输入序列中的哪些部分,然后根据关注的区域来产生下一个输出,如此往复。模型的大概示意图如下所示
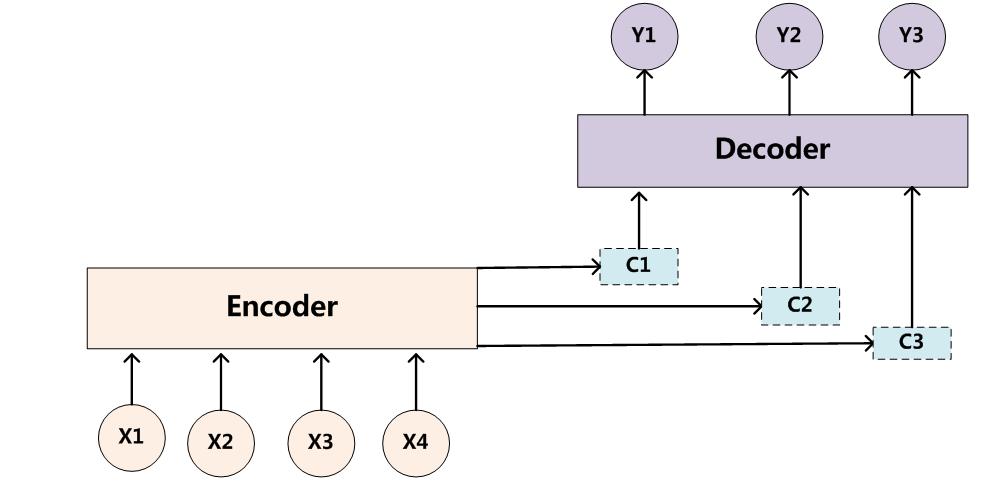
相比于之前的encoder-decoder模型,attention模型最大的区别就在于它不在要求编码器将所有输入信息都编码进一个固定长度的向量之中。相反,此时编码器需要将输入编码成一个向量的序列,而在解码的时候,每一步都会选择性的从向量序列中挑选一个子集进行进一步处理。这样,在产生每一个输出的时候,都能够做到充分利用输入序列携带的信息。而且这种方法在翻译任务中取得了非常不错的成果。
在这篇文章中,作者提出了一个用于翻译任务的结构。解码部分使用了attention模型,而在编码部分,则使用了BiRNN(bidirectional RNN,双向RNN)
2.1 解码
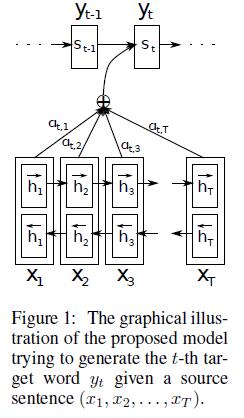
我们先来看看解码。解码部分使用了attention模型。类似的,我们可以将之前定义的条件概率写作
上式si表示解码器i时刻的隐藏状态。计算公式是
注意这里的条件概率与每个目标输出yi相对应的内容向量ci有关。而在传统的方式中,只有一个内容向量C。那么这里的内容向量ci又该怎么算呢?其实ci是由编码时的隐藏向量序列(h1,…,hTx)按权重相加得到的。
由于编码使用了双向RNN,因此可以认为hi中包含了输入序列中第i个词以及前后一些词的信息。将隐藏向量序列按权重相加,表示在生成第j个输出的时候的注意力分配是不同的。αij的值越高,表示第i个输出在第j个输入上分配的注意力越多,在生成第i个输出的时候受第j个输入的影响也就越大。那么现在我们又有新问题了,αij又是怎么得到的呢?这个其实是由第i-1个输出隐藏状态si?1和输入中各个隐藏状态共同决定的。也即是
也就是说,si?1先跟每个h分别计算得到一个数值,然后使用softmax得到i时刻的输出在Tx个输入隐藏状态中的注意力分配向量。这个分配向量也就是计算ci的权重。我们现在再把公式按照执行顺序汇总一下:
上面这些公式就是解码器在第i个时间段内要做的事情。作者还给了一个示意图:
2.2 编码
相比于上面解码的创新,这边的编码就比较普通了,只是传统的单向的RNN中,数据是按顺序输入的,因此第j个隐藏状态h→j只能携带第j个单词本身以及之前的一些信息;而如果逆序输入,则h←j包含第j个单词及之后的一些信息。如果把这两个结合起来,hj=[h→j,h←j]就包含了第j个输入和前后的信息。
3.实验结果
为了检验性能,作者分别使用传统模型和attention模型在英语-法语的翻译数据集上进行了测验。
传统模型的编码器和解码器各有1000个隐藏单元。编码器中还有一个多层神经网络用于实现从隐藏状态到单词的映射。在优化方面,使用了SGD(minibatch stochastic gradient descent)以及Adadelta,前者负责采样,后者负责优化下降方向。
得到的结果如下:
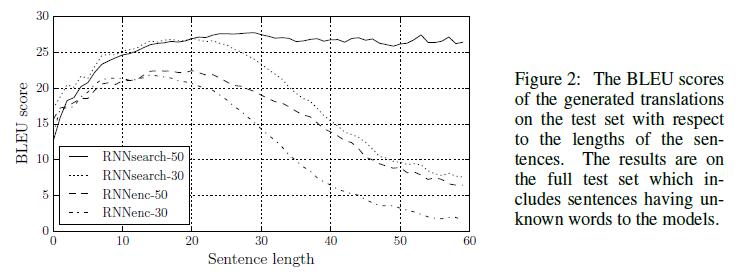
图中RNNenc表示传统的结构,而RNNsearch表示attention模型。后面的数字表示序列的长度。可以看到,不论序列长度,attention模型的性能均优于传统的编码-解码模型。而RNNsearch-50甚至在长文本上的性能也非常的优异
除了准确度之外,还有一个很值得关注的东西:注意力矩阵。之前已经提过,每个输出都有一个长为Tx的注意力向量,那么将这些向量合起来看,就是一个矩阵。对其进行可视化,得到如下结果
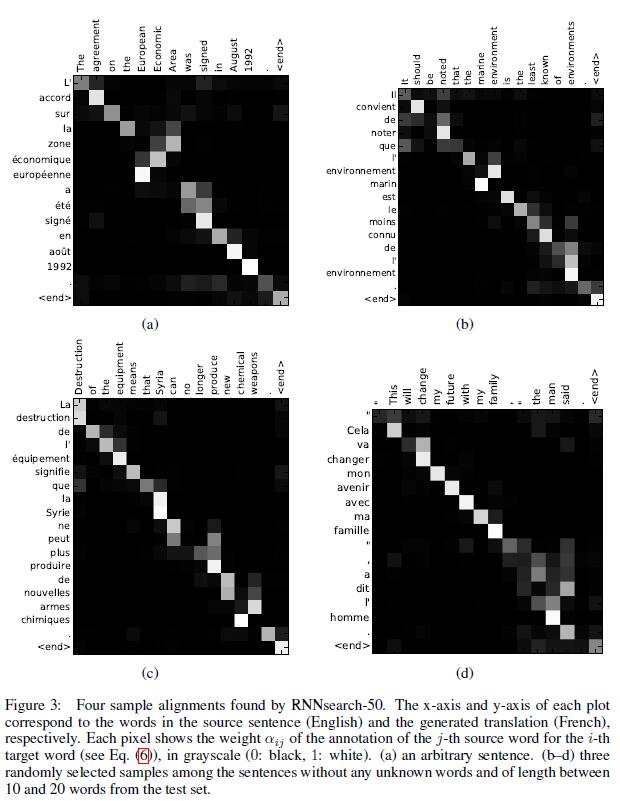
其中x轴表示待翻译的句子中的单词(英语),y轴表示翻译以后的句子中的单词(法语)。可以看到尽管从英语到法语的过程中,有些单词的顺序发生了变化,但是attention模型仍然很好的找到了合适的位置。换句话说,就是两种语言下的单词“对齐”了。因此,也有人把注意力模型叫做对齐(alignment)模型。而且像比于用语言学实现的硬对齐,这种基于概率的软对齐更加优雅,因为能够更全面的考虑到上下文的语境。