这道题不知道这个定理很难做出来。
除非暴力找规律。
我原本找的时候出了问题
暴力找出的从13及以上的答案就有问题了
因为13的12次方会溢出
那么该怎么做?
快速幂派上用场。
把前几个素数的答案找出来。
然后因为原根的一个条件是与p互质,所以可以把欧拉函数的值求出来尝试一下
打印出来,就可以发现规律
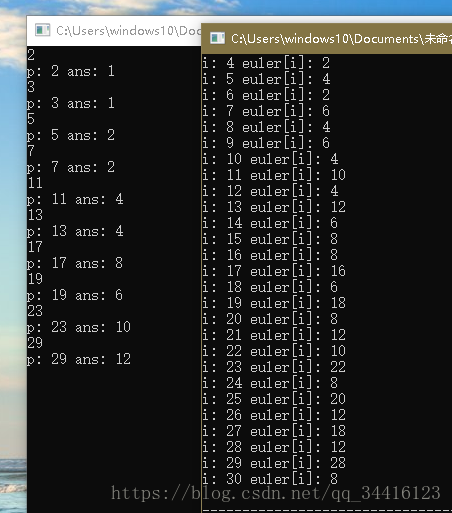
答案就是phi(p-1)
暴力找答案代码
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cctype>
#define REP(i, a, b) for(int i = (a); i < (b); i++)
#define _for(i, a, b) for(int i = (a); i <= (b); i++)
using namespace std;typedef long long ll;
const int MAXN = 21234567;
bool vis[MAXN];void read(ll& x)
{int f = 1; x = 0; char ch = getchar();while(!isdigit(ch)) { if(ch == '-') f = -1; ch = getchar(); }while(isdigit(ch)) { x = x * 10 + ch - '0'; ch = getchar(); }x *= f;
}ll cal(ll a, ll b, ll p)
{ll ret = 1 % p; a %= p;while(b){if(b & 1) ret = (ret * a) % p;b >>= 1;a = (a * a) % p;}return ret;
}int main()
{while(1){ll p;read(p);int ans = 0;_for(x, 1, p - 1){memset(vis, 0, sizeof(vis));_for(i, 1, p - 1){ll t = cal(x, i, p);if(vis[t] || t == 0) break;vis[t] = 1;if(i == p - 1) ans++;} }printf("p: %d ans: %d\n", p, ans);}return 0;
}求欧拉函数值代码
#include<cstdio>
#include<cctype>
#define REP(i, a, b) for(int i = (a); i < (b); i++)
#define _for(i, a, b) for(int i = (a); i <= (b); i++)
using namespace std;typedef long long ll;
const int MAXN = 21234567;ll euler(ll x)
{ll ret = x;for(int i = 2; i * i <= x; i++)if(x % i == 0){ret = ret / i * (i - 1);while(x % i == 0) x /= i;if(x == 1) break;}if(x > 1) ret = ret / x * (x - 1);return ret;
}void read(ll& x)
{int f = 1; x = 0; char ch = getchar();while(!isdigit(ch)) { if(ch == '-') f = -1; ch = getchar(); }while(isdigit(ch)) { x = x * 10 + ch - '0'; ch = getchar(); }x *= f;
}int main()
{_for(i, 1, 30) printf("i: %d euler[i]: %lld\n", i, euler(i));return 0;
}AC代码
#include<cstdio>
#include<cctype>
#define REP(i, a, b) for(int i = (a); i < (b); i++)
#define _for(i, a, b) for(int i = (a); i <= (b); i++)
using namespace std;typedef long long ll;
const int MAXN = 21234567;ll euler(ll x)
{ll ret = x;for(int i = 2; i * i <= x; i++)if(x % i == 0){ret = ret / i * (i - 1);while(x % i == 0) x /= i;if(x == 1) break;}if(x > 1) ret = ret / x * (x - 1);return ret;
}void read(ll& x)
{int f = 1; x = 0; char ch = getchar();while(!isdigit(ch)) { if(ch == '-') f = -1; ch = getchar(); }while(isdigit(ch)) { x = x * 10 + ch - '0'; ch = getchar(); }x *= f;
}int main()
{ll n, x; read(n);while(n--){read(x);printf("%lld\n", euler(x-1));}return 0;
}